Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по геометрии на тему Теорема Пифагора

Содержание

2. Теорема Пифагора
3. Кто такой Пифагор?Для нас он прежде всего
4. Теорема Пифагора Квадрат гипотенузы прямоугольного треугольника
5. Теорема невестыДанную теорему, носящую в литературе имя
7. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах.
9. ДоказательствоSкв=(a+b)2 Sкв=4.1/2 a .b +с2(a+b)2 =4.1/2 a .b +с2с2 =a2 +b2аbcbbbаааccc
10. А.Шамиссо Пребудет вечной истина, как скороВсе познает
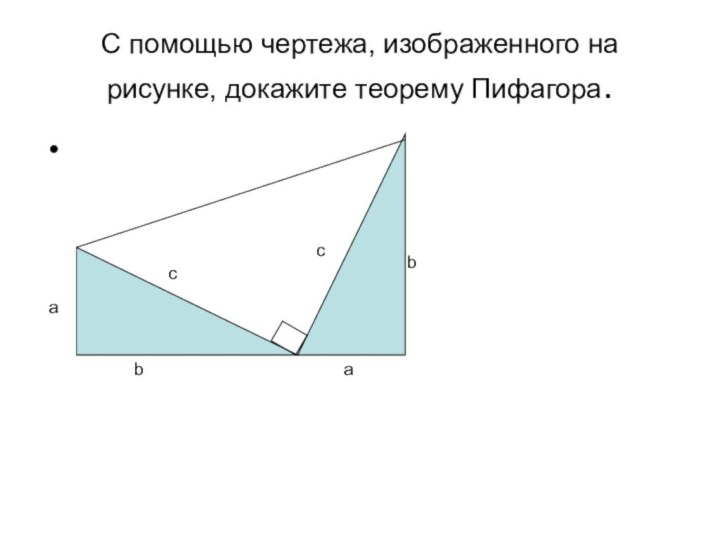
11. С помощью чертежа, изображенного на рисунке, докажите
12. Доказательство(a+b)*(a+b)/2=1/2c*c+1/2a*b+1/2a*b(a2+2ab+b2)/2=1/2(2ab+c2)a2+2ab+b2=2ab+c2a2+b2=c2
13. 43x53x86yABCРис.1Рис.2Рис. 3Рис.4
14. Обратная теорема:Если в треугольнике квадрат одной стороны
15. Задача перваяСлучися некому человеку к стене лествицу
16. Задача втораяНа берегу реки рос тополь одинокий.Вдруг
17. Скачать презентацию
18. Похожие презентации

Теорема Пифагора

Главная
Математика
Презентация по геометрии на тему Теорема Пифагора

Кто такой Пифагор?Для нас он прежде всего математик. Рассказывают, что когда Пифагора

Теорема Пифагора Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.c2=a2 +

Теорема невестыДанную теорему, носящую в литературе имя Пифагора, в средневековье в некоторых

Презентация по геометрии на тему Теорема Пифагора

Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах.

ДоказательствоSкв=(a+b)2 Sкв=4.1/2 a .b +с2(a+b)2 =4.1/2 a .b +с2с2 =a2 +b2аbcbbbаааccc

А.Шамиссо Пребудет вечной истина, как скороВсе познает слабый человек!И ныне теорема ПифагораВерна,

С помощью чертежа, изображенного на рисунке, докажите теорему Пифагора.

Доказательство(a+b)*(a+b)/2=1/2c*c+1/2a*b+1/2a*b(a2+2ab+b2)/2=1/2(2ab+c2)a2+2ab+b2=2ab+c2a2+b2=c2

Обратная теорема:Если в треугольнике квадрат одной стороны равен сумме квадратов двух других

Задача перваяСлучися некому человеку к стене лествицу прибрати, стены же тоя высота

Задача втораяНа берегу реки рос тополь одинокий.Вдруг ветра порыв его ствол надломал.Бедный

Слайды презентации

Слайд 2 Теорема Пифагора

Слайд 3 Кто такой Пифагор?
Для нас он прежде всего математик.

Кто такой Пифагор?Для нас он прежде всего математик. Рассказывают, что когда

Рассказывают, что когда Пифагора спросили, кто он такой ,

он с гордостью произнес никогда тогда неведомое слов : философ. Родился он около 580 года до нашей эры на острове Самосе, у самых берегов Малой Азии (Ионии) Отец его был художником и гравером при дворце самосского правителя. Совсем юным он покинул Родину. Сначала приплыл к берегам Египта, прошел его вдоль и поперек. Затем попал в плен к персидскому завоевателю, и его увезли в Вавилон. Вернувшись на Родину, он создает свою школу.Чтобы поднять авторитет учителя, все открытия приписывались самому Пифагору.Он составляет таблицу расположения звезд. Изучает свойства чисел: простые, составные, четные, нечетные.Открывает рациональные числа.

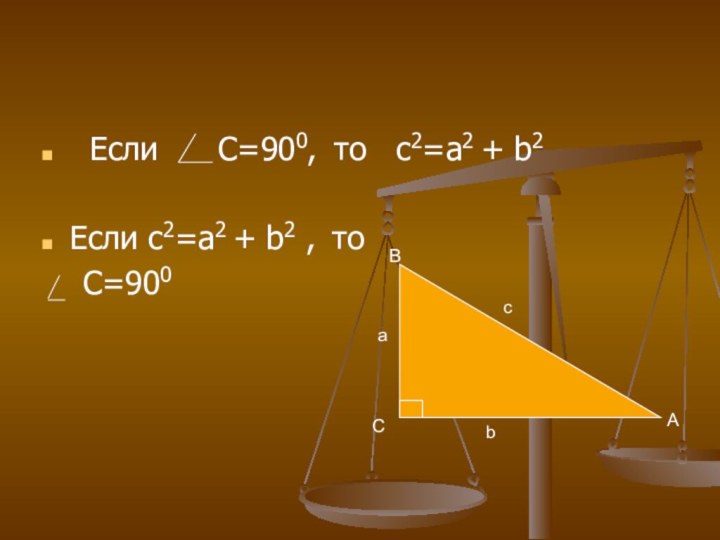
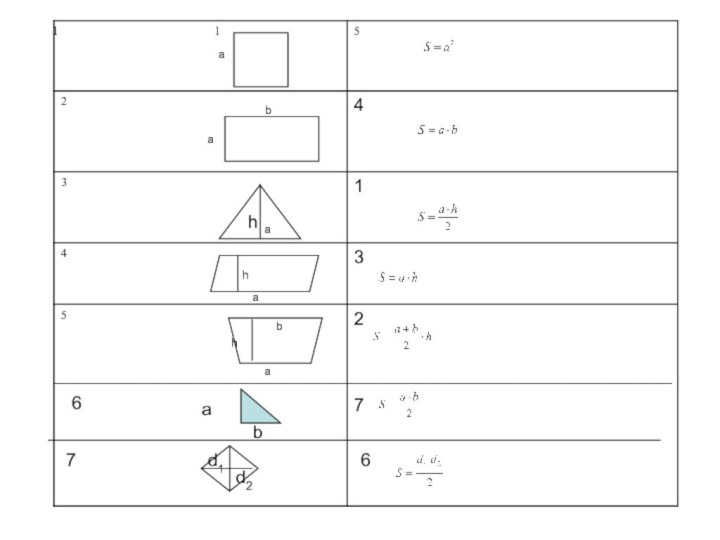
Слайд 4 Теорема Пифагора
Квадрат гипотенузы прямоугольного треугольника равен сумме

квадратов катетов.

c2=a2 + b2

Слайд 5 Теорема невесты
Данную теорему, носящую в литературе имя Пифагора,

Теорема невестыДанную теорему, носящую в литературе имя Пифагора, в средневековье в

в средневековье в некоторых областях Германии и Франции называли

«мостом ослов» , а за трудность доказательства, приведенного в книге Евклида «Начала», -»бегством несчастного». У математиков арабского Востока она называлась «теоремой невесты». Дело в том, что в некоторых списках «Начал» Евклида эта теорема называлась «теоремой нимфы» за сходство чертежа с пчелкой, бабочкой, по –гречески с нимфой. При переводе с греческого арабский переводчик перевел «нимфа» как «невеста»

Слайд 6

Слайд 7 Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме

квадратов, построенных на катетах.

Слайд 8

Слайд 9 Доказательство
Sкв=(a+b)2
Sкв=4.1/2 a .b +с2
(a+b)2 =4.1/2 a .b

+с2
с2 =a2 +b2

а
b
c
b
b
b
а
а
а
c
c
c

Слайд 10 А.Шамиссо
Пребудет вечной истина, как скоро
Все познает слабый человек!
И

А.Шамиссо Пребудет вечной истина, как скороВсе познает слабый человек!И ныне теорема

ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно

было жертвоприношение
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За свет луча, пришедший с облаков.
Поэтому всегда с тех самых пор
Чуть истина рождается на свет,
Быки ревут, ее почуяв, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.

Слайд 11 С помощью чертежа, изображенного на рисунке, докажите теорему

Пифагора.

Слайд 12 Доказательство
(a+b)(a+b)/2=1/2cc+1/2ab+1/2ab
(a2+2ab+b2)/2=1/2(2ab+c2)
a2+2ab+b2=2ab+c2
a2+b2=c2

Слайд 13
4
3
x
5
3
x

8
6
y

A
B
C
Рис.1
Рис.2
Рис. 3
Рис.4

Слайд 14 Обратная теорема:
Если в треугольнике квадрат одной стороны равен

Обратная теорема:Если в треугольнике квадрат одной стороны равен сумме квадратов двух

сумме квадратов двух других сторон , то такой треугольник

прямоугольный.
Дано:
Док-ть: с=900

А1

С1

В1

АВ2=ВС2+АС2

А 1В 12=В 1С 12+А 1С 12

АВС = А1В1С1

С = С1

АВ2=ВС2+АС2

Слайд 15 Задача первая
Случися некому человеку к стене лествицу прибрати,

Задача перваяСлучися некому человеку к стене лествицу прибрати, стены же тоя

стены же тоя высота есть 117 стоп. И обрете

лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать.

Слайд 16 Задача вторая
На берегу реки рос тополь одинокий.
Вдруг ветра

Задача втораяНа берегу реки рос тополь одинокий.Вдруг ветра порыв его ствол

порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С

теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?