Слайд 2
Работа в парах
Длины отрезков: АВ= 3,1 см; СЕ=1,5
см; ОН=1,8 см.
Единицы измерения отрезков: мм, см, дм, м
и т.д.
Число, выражающее длину отрезка всегда положительное.
Слайд 3
Работа в тетрадях
№ 714 Какие из отрезков АВ,
МР, CD, ОК, EF равны, если АВ=3 см, МР=5см,
CD=30 мм, ОК=50 мм, ЕF=84см
Ответ: АВ=CD
МР=ОК
Решение: 1 см=10 мм, 3 см=30 мм, 5 см=50 мм
АВ=CD=3см=30мм
МР=ОК=5 см=50мм
Слайд 4
Повторение (устно)
Повторим фигуры, которые вы изучали ранее и
уже знаете.
1 квадрат
2 особый случай треугольника – прямоугольный треугольник
3
круг
4 треугольник
5 трапеция
6 прямоугольник
Квадрат – это прямоугольник, у которого все стороны равны
Слайд 5
Работа в парах
Найдите среди данных фигур равные
Фигуры называются
равными, если их можно совместить наложением
Слайд 7
определение
Площадь – это величина той части плоскости, которую
занимает фигура.
Единицы измерения площади: см^2, м^2, мм^2, дм^2, км^2.
Слайд 8
Метод палетки
Эта пластинка накладывается на фигуру, площадь которой
требуется измерить
Сначала подсчитывается число квадратов, полностью укладывающихся в
данной фигуре; на чертеже их 26. Затем подсчитывается число квадратов, пересекаемых контуром фигуры; на чертеже их 21.
Каждый из неполных квадратов принимается за половину квадрата, таким образом 21 : 2 = 10,5 квадрата.
26 + 10,5 = 36,5 квадрата. Если, например, каждый квадрат в действительности соответствует 1 кв. м, то измеряемая площадь составит 36,5 кв. м.
Слайд 9
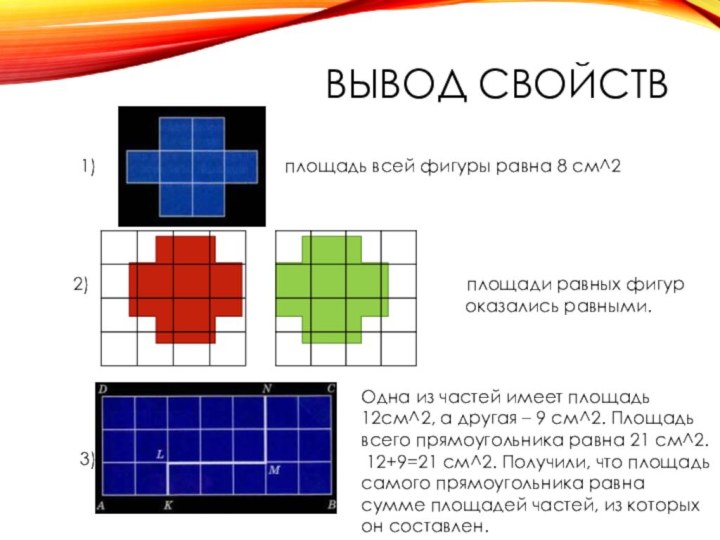
Вывод Свойств
1)
площадь всей фигуры равна 8 см^2
2) площади равных фигур
оказались равными.
Одна из частей имеет площадь 12см^2, а другая – 9 см^2. Площадь всего прямоугольника равна 21 см^2.
12+9=21 см^2. Получили, что площадь самого прямоугольника равна сумме площадей частей, из которых он составлен.
3)
Слайд 10
Формулировка свойств
Если какую-нибудь фигуру можно разбить на р
квадратов со стороной 1 см, то ее площадь равна
р см^2
Площади равных фигур равны.
Площадь всей фигуры равна сумме площадей ее частей
Слайд 11
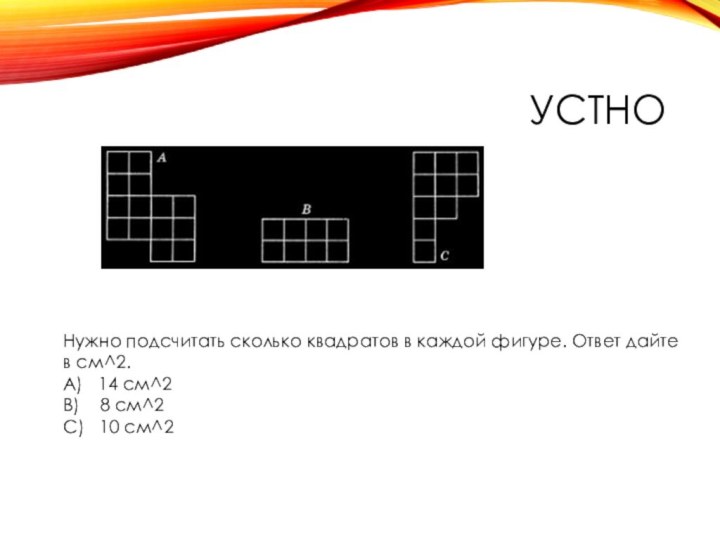
устно
Нужно подсчитать сколько квадратов в каждой фигуре. Ответ
дайте в см^2.
А) 14 см^2
В) 8 см^2
С)
10 см^2
Слайд 12
Работа в парах
Мы накладываем палетку на фигуру и
считаем количество квадратов. Сначала целых, а затем тех, что
не полностью поместились в фигуру, считая их, как половина квадрата
Считаем квадраты: полных 6, неполных 8, 8:2=4. Получаем, что площадь всей фигуры 6+4= 10.
Ответ: 10 кв. ед.
Слайд 13
Устно
№ 710 Равны ли друг другу листы одной
тетради? Почему?
Равны, потому что при наложении они совпадают. Нет
в тетради листов, которые больше или наоборот гораздо меньше, чем остальные.
Еще один способ, которым это можно доказать, это посчитать (например в тетради в клеточку) все клеточки, их должно быть одинаковое количество на всех страницах.
Слайд 14
прямоугольник
Площадь равна 15 см^2
Весь прямоугольник состоит из 5*3=15
таких квадратов. Его площадь равна 15 см^2
Площадь прямоугольника обозначим
буквой S, его длину буквой – а, а ширину – b. Получаем формулу площади прямоугольника:
S=a*b
Слайд 15
Работа В тетрадях
№ 717 Длина прямоугольника 28 см,
а его ширина в 7 раз меньше. Чему равна
площадь прямоугольника?
Чтобы найти площадь прямоугольника нужно знать его длину и ширину.
Чтобы найти ширину, разделим длину на 7:
28:7=4 (см) – ширина прямоугольника
Теперь воспользуемся формулой нахождения площадь прямоугольника:
S= 28*4=96 (см^2)
Ответ: 96 см^2
Слайд 16
квадрат
Квадрат – это прямоугольник с равными сторонами.
Его площадь
равна 4*4=4^2 см^2=16см^2
Если сторона квадрата равна а, то площадь
S квадрата равна a*a=a^2. И формула нахождения площади квадрата имеет вид: S=a^2.
Именно поэтому запись a^2 называют квадратом числа.
Слайд 17
Работа в тетрадях
№ 721 Приведите примеры неравных фигур,
имеющих равные площади.
Например:
Прямоугольник с длинной 6 см, а шириной
5 см и прямоугольник с длиной 15 и шириной 2
Площадь 1-ого: 5*6=30 см^2
Площадь 2-ого: 15*2=30 см^2
Прямоугольник с длиной 9 см, а шириной 4 см и квадрат со стороной 6 см
Площадь прямоугольника: 9*4=36 см^2
Площадь квадрата: 6*6=36 см^2
Слайд 18
Домашнее задание
Записи в тетради учить, прочитать п. 18;
ст 110-111 № 712, 716, 719, 722