Презентация на тему Начертательная геометрия. Пересечение плоскостей

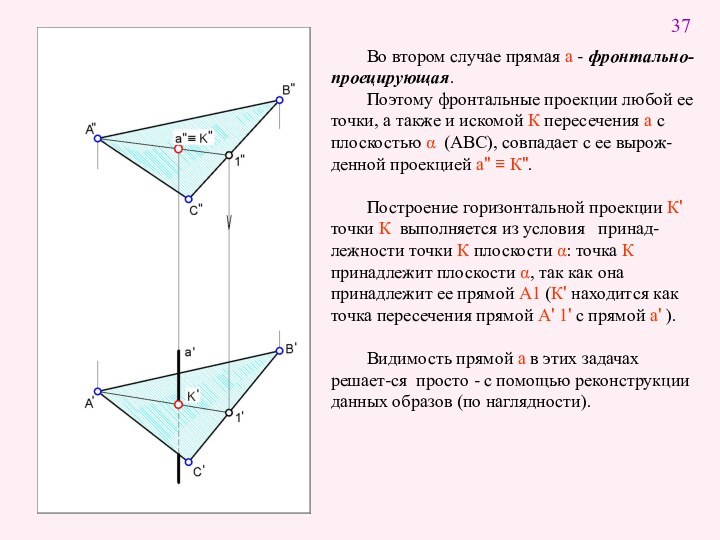
точку К пересечения данной прямой а с плоскостью α.

Определить видимость прямой.

Символическая запись алгоритма

Определить видимость прямой a по правилу конкурирующих точек

Решение задачи выполняется в три этапа.

2

31

на пространственном рисунке и при проецировании всех элементов задачи

на плоскости П.

Геометрические образы (пл. АВС, прямая а) спроецированы на плоскость П.

32

а с плоскостью АВС.
Выполняем 3-й этап алгоритма
34

построение точки К пересечения прямой а с плоскостью α.

Возможны три варианта условия данной задачи:
- прямая а - общего положения, плоскость α - проецирующая (или уровня);
- прямая а - проецирующая, плоскость α - общего положения;
- прямая а - общего положения, плоскость α - общего положения.

Решение первых двух задач можно выполнить, не применяя алгоритма, так как один из заданных образов частного положения.

35

проецирующая.
Поэтому горизонтальная проекция К1 искомой точки К определяется как

точка пересечения линейной проекции А'В'С' плоскости α с горионтальной проекцией а1 данной прямой а.
Фронтальная проекция К2 точки К строится из условия принадлежности точки К прямой а.

36

проекции любой ее точки, а также и искомой К

пересечения а с плоскостью α (АВС), совпадает с ее вырож-денной проекцией a" ≡ К".

Построение горизонтальной проекции К' точки К выполняется из условия принад-лежности точки К плоскости α: точка К принадлежит плоскости α, так как она принадлежит ее прямой A1 (К' находится как точка пересечения прямой A' 1' с прямой а' ).

Видимость прямой а в этих задачах решает-ся просто - с помощью реконструкции данных образов (по наглядности).

37

пересечения прямой а с плоскостью α (c//d) выполнено по

описан-ному алгоритму.
1) прямую а заключают во вспомогательную горизонтально проецирующую плоскость- посредник Σ(Σ1);
2) строят прямую m пересечения плоскостей α (c//d) и Σ(Σ1). На чертеже это отразится записью (a1≡ Σ1≡ m1 ). Фронтальную проекцию m2 строят из условия ее принадлежности данной плоскости α(m и α имеют общие точки 1 и 2);
3) находят точку K2 , как результат пересече-ния a2 с m2, а K1 строят по принадлежности прямой m1. Точка K(K2, K1) - искомая точка пересечения прямой a с плоскостью α (c//d).

38

точек. Так, на плоскости Н видимость определена с помощью

горизон-тально конкурирующих точек 1 и 3(11≡31), где точка 1 принадлежит плоскости α а точка 3 - прямой a. Точка 3 расположена над точкой 1, поэтому точка 3 и прямая a в этом участке на плоскости П1 будет видима.
На фронтальной плоскости видимость может быть определена или с помощью пары фронтально-конкурирующих точек, или по реконструкции данных образов (при восхо-дящей плоскости видимость одинаковая на плоскостях П1 и П2).
Данная задача после определения види-мости прямой а имеет вид данного рисунка.

39

Для определения точек линии пересечения обе заданные плоскости α

и β пересекают двумя
вспомогательными (параллельными между собой) плоскостями-посредник. Некоторое
упрощение можно достичь, если вспомогательные плоскости проводить через прямые,
задающие плоскость.
Рассмотрим пример. Плоскость α задана (ABC), плоскость β задана (DEK). Точки M и N,
определяющие искомую линию пересечения двух данных плоскостей найдем как точки
пересечения каких-либо двух сторон (как две прямые) треугольника ABC с плоскостью другого
треугольника DEK, т.е. дважды решим позиционную задачу на определение точки пересечения
прямой с плоскостью по рассмотренному алгоритму.
Выбор сторон треугольников произволен, так как только построением можно точно определить,
какая действительно сторона и какого треугольника пересечет плоскость другого. Выбор
плоскости-посредник также произволен, так как прямую общего положения, какими являются
все стороны треугольников ABC и DEK, можно заключить в горизонтально проецирующую
или во фронтально проецирующую плоскости.

42

задачи на определение линии MN пересечения двух плос-костей ABC

и DEK.

43

построения точки M использована горизонтально проецирующая плоскость - посредник

Σ (Σ 1), в которую заключена сторона AB ∆ ABC (AB ⊂ α).
1. Обозначаем горизонтально проецирующую плоскость - Σ

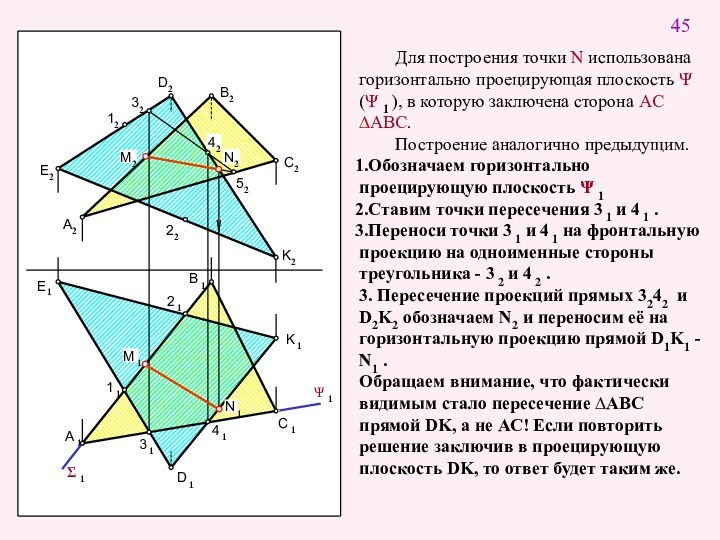
2-й этап решения
Строим линию пересечения (на чертеже она задана точками 1 и 2) плоскости-посредника Σ (Σ1) и плоскости DEK.
2. Ставим точки пересечения на плоскости П1 - 11 и 21 и переносим их на П2 на одноименные стороны треугольника- 12 и 22 Соединяем точки 12 и 22 тонкой линией.

3-й этап решения
Находим точку M пересечения прямой 1 - 2 с прямой AB.
3. Пересечение проекций прямых 1222 и А2В2 обозначаем М2 и переносим её на горизонтальную проекцию прямой А1В1 - М1

Найдена одна точка M искомой линии пересечения.

44

N использована горизонтально проецирующая плоскость Ψ (Ψ 1 ),

в которую заключена сторона AC ∆ABC.
Построение аналогично предыдущим.
Обозначаем горизонтально проецирующую плоскость Ψ 1
Ставим точки пересечения 3 1 и 4 1 .
Переноси точки 3 1 и 4 1 на фронтальную проекцию на одноименные стороны треугольника - 3 2 и 4 2 .
3. Пересечение проекций прямых 3242 и D2K2 обозначаем N2 и переносим её на горизонтальную проекцию прямой D1K1 - N1 .
Обращаем внимание, что фактически видимым стало пересечение ∆ABC прямой DK, а не АС! Если повторить решение заключив в проецирующую плоскость DK, то ответ будет таким же.

45

выполнено с помощью горизонтально конкурирующих точек. Смотрим на горизонтальную

проекцию скрещивающихся прямых АС и DК. На прямой АС есть точка 4, на проекции прямой DK ставим точку 8 (41 ≡81).
Точка 4 расположена над точкой 8 (42 и 82), поэтому на плоскости П1 часть треугольника DEK, расположенная в сторону точки 4, закрывает собой часть треугольника ABC, расположенную от линии пересечения в сторону точки 8.
С помощью пары фронтально конку-рирующих точек 6 и 7 (62≡72) определена видимость на плоскости П2.
Невидимые линии проводим тонкой штриховой линией, а видимые толстой основной.

46

Направление взгляда для определения видимости на П1

том, что заданная
фигура неподвижна, а одна из основных

плоскостей V или H заменяется новой
дополнительной плоскостью V1 или H1,
расположенной параллельно или пер-
пендикулярно заданной геометрической
фигуре. Точка A задана в системе V/H.
Плоскость V замерена новой плоскостью
V1 перепендикулярной H. Плоскость H
является общей в системе V/H и H/V1,
то координата zA остается неизменной.
Следовательно, расстояние от новой
фронтальной проекции до новой оси x1
равно расстоянию от заменяемой
проекции до оси x.

47

вращают вокруг оси x1
до совмещения с плоскостью H.

Новая фронтальная проекция A1" точки А окажется на общем перпендикуляре
к новой оси x1 с оставшейся без изменения ее проекции A'.

42

1.
Преобразовать чертеж так, чтобы
прямая общего положения оказалась

параллельной одной из плоскостей
проекций

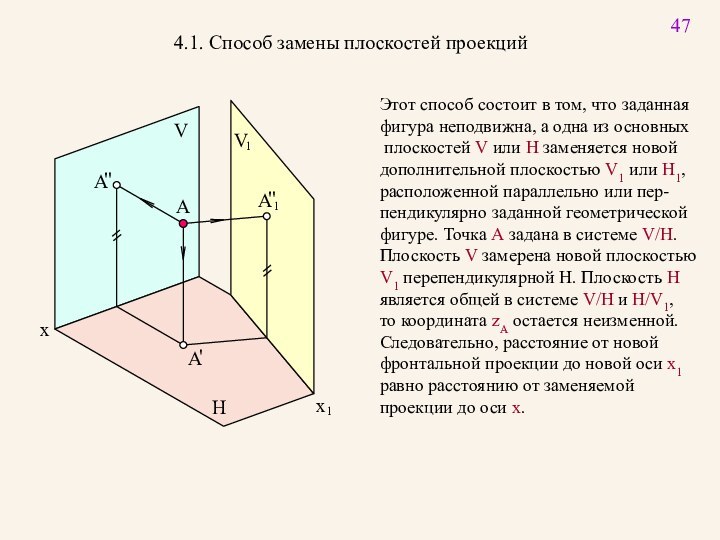
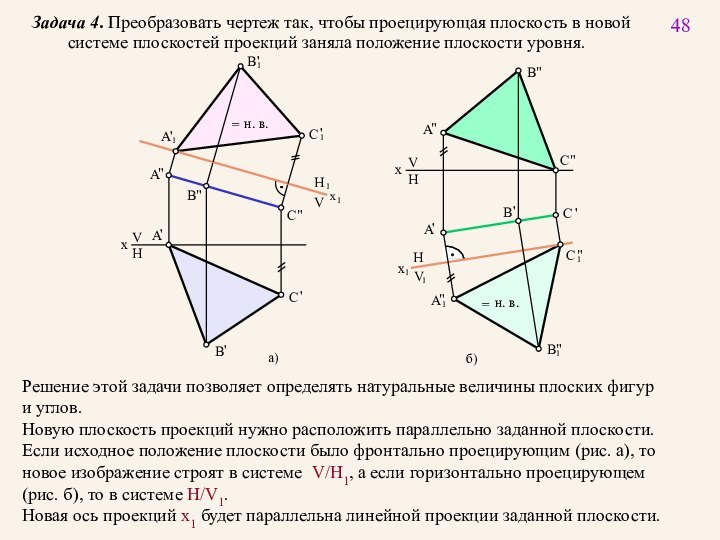
Новую проекцию прямой, отвечающую поставленной задачи, можно построить на
новой плоскости проекций V1 , расположив ее параллельно самой прямой и перпенди-
кулярно плоскости H, т.е. от системы плоскостей V/H с осью проекций x следует
перейти к системе H/V1 с новой осью x1.

a', новые линии связи A'A1"
и B'B1" проведены перпендикулярно

оси x1. Новые фронтальные проекции A1" и B1"
точек A и B получают, измерив от оси x на поле V координаты высот zA и zB,
отложив их от оси x1 на новое поле V1.
Новая проекция a1" дает натуральную величину отрезка AB и угол α наклона его
к плоскости H.
Угол наклона прямой a к плоскости V можно определить, построив изображение
прямой на другой дополнительной плоскости H1 V, где H1// a.

x

H

V

x

H

V

H

α

V

β

а)

б)

положения
в новой системе плоскостей проекций стала проецирующей.
Для этого

в плоскости ABC проведена горизонталь h. Новая плоскость проекций V1
расположена перпендикулярно H. Горизонталь на поле V1 изобразится точкой, а вся
плоскость прямой линией C1"A1" B1" с углом α, который определяет угол наклона
плоскости ABC к плоскости H (рис.а).
Построив изображение плоскости в системе V/H1, где H1 расположена перпендикулярно
фронтали f (рис. б) плоскости, можно определить угол β наклона ABC к плоскости V.