Презентация на тему по математике на тему Центральные и вписанные углы (8 класс)

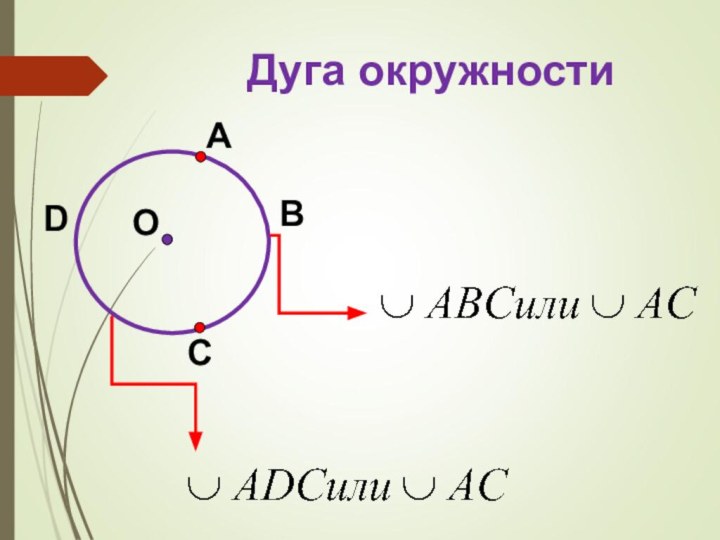
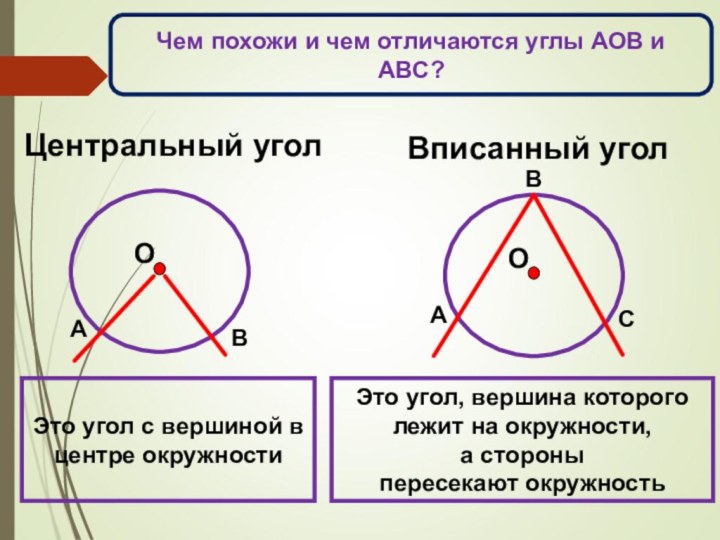
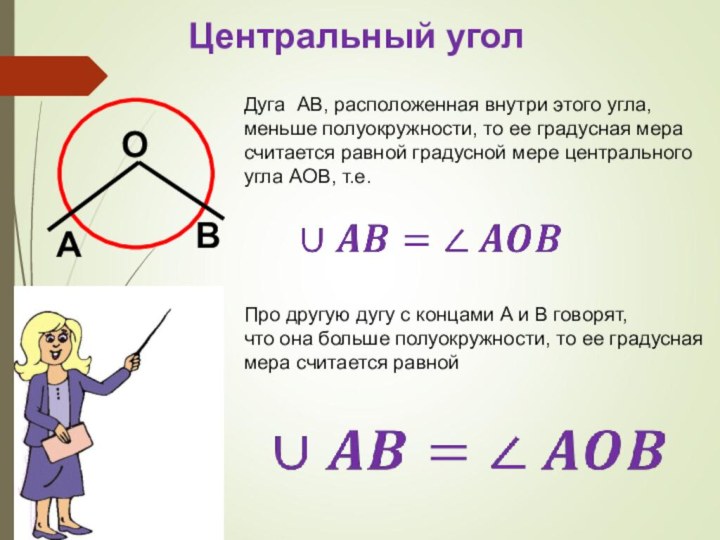
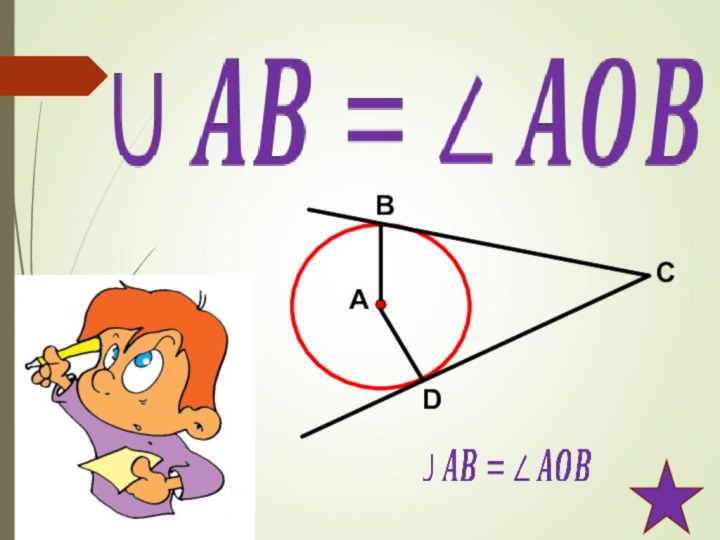центрального угла.
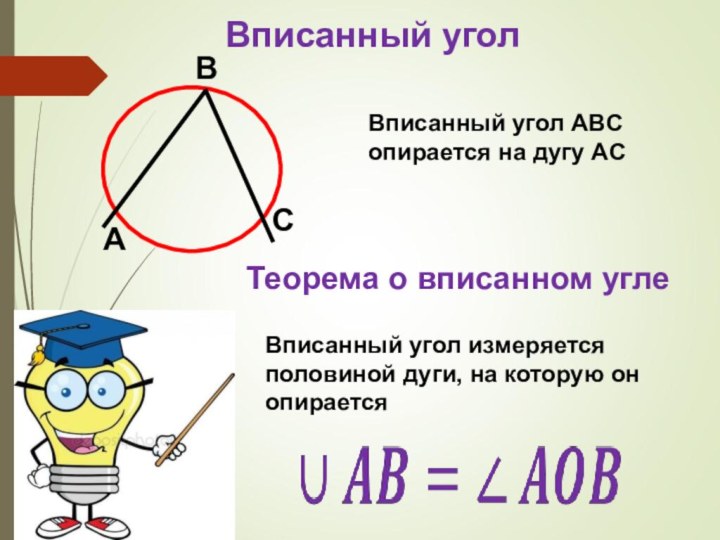
2. Ввести понятие вписанного угла.
3.

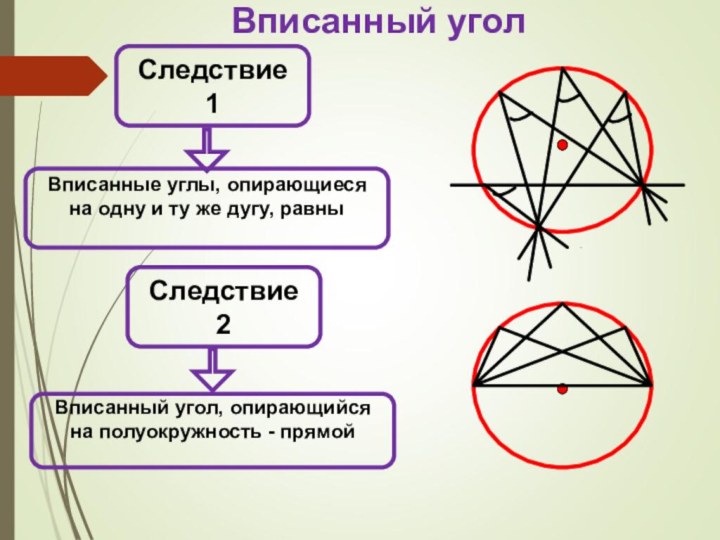
Рассмотреть теорему о вписанном угле
и следствия из нее.

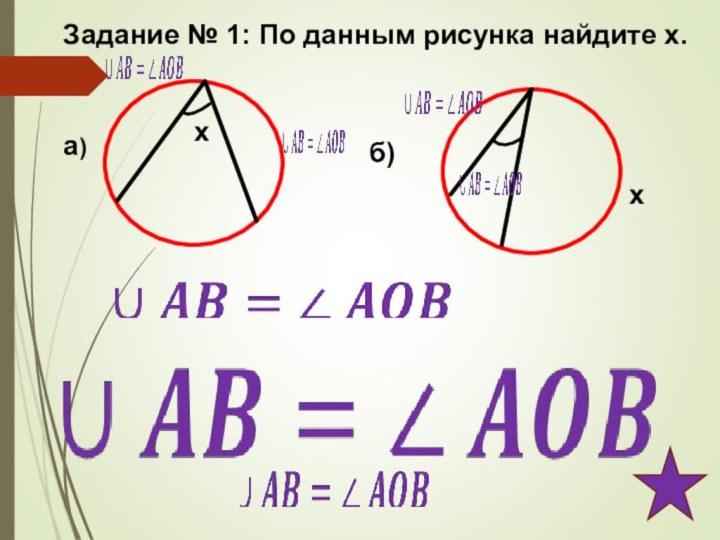
4. Показать применение теоремы о вписанном угле
и следствий из нее при решении задач.

5. Научить решать задачи на вычисления
градусной меры дуги окружности.

диаметром окружности


О


A
B
L
AB - диаметр
M

ABC?
Это угол с вершиной в
центре окружности
Это угол, вершина которого

лежит на окружности,
а стороны
пересекают окружность

A

B

A

B

C

Центральный угол

Вписанный угол

то ее градусная мера
считается равной градусной мере центрального
угла AOB,

т.е.

Центральный угол

Про другую дугу с концами A и B говорят,
что она больше полуокружности, то ее градусная
мера считается равной

 

 

центром в точке A?
A
P
M
E
K
C
Центральный угол
 

о вписанном угле
Вписанный угол измеряется
половиной дуги, на которую

он опирается

 

же дугу, равны

Следствие 2
Вписанный угол, опирающийся
на полуокружность -

прямой

Вписанный угол

вписанными?

 

x.

а)

x
 
 
б)

 

 
x
 
 

окружность на дуги в отношении 2:3:4. Найдите больший угол

треугольника ABC.

 

 

B

P

A

C

M

 

называется полуокружностью,
какая дуга меньше полуокружности, а какая больше?
Какой

угол называется вписанным?

Сформулируйте теорему
о вписанном угле.

Сформулируйте следствия,
вытекающие из теоремы о
вписанном угле.

теорию),
вопросы стр. 187 №8 -13 (устно);
учебник № 650,

№ 652, №655;
рабочая тетрадь № 86, №88

/ Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 12-е изд.,

 – М.: Просвещение, 2002 г.
Зив Б.Г., Мейлер В.М., Дидактические материалы по геометрии для 8 класса. – 6-е изд. – М.: Просвещение, 2002 г.
Смирнова И.М., Смирнов В.А. Устные упражнения по геометрии для 7–11 классов. Книга для учителя. М.; Просвещение, 2003 г.
Рабинович Е.М. Задачи и упражнения на готовых чертежах. Геометрия  7–9 классы. «Илекса», «Гимназия», Москва-Харьков, 2003 г.