Слайд 2
Главная страница
Аксиоматика планиметрии Вейля.
Аксиоматика планиметрии Гильберта.
Аксиоматика линейного пространства.
Аксиоматика
метрического пространства.
Аксиоматика топологического пространства
Аксиоматика натуральных чисел Пеано.
Контрпример к аксиоматике
Вейля.
Контрпример к аксиоматике Гильберта.
Контрпример к аксиоматике линейного пространства.
Контрпример к аксиоматике метрического пространства.
Контрпример к аксиоматике топологического пространства.
Контрпример к аксиоматике Пеано.
Слайд 3
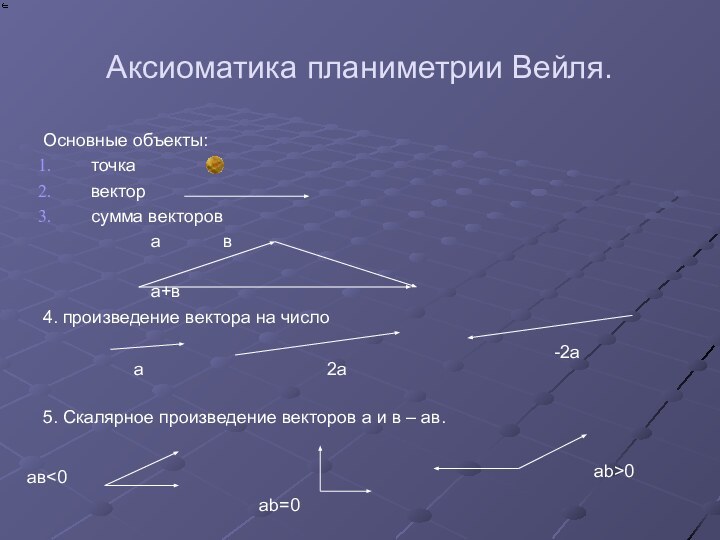
Аксиоматика планиметрии Вейля.
Основные объекты:
точка
вектор
сумма векторов
а
в
а+в
4. произведение вектора на число
5. Скалярное произведение векторов а
и в – ав.
а
2а
-2а
aв<0
ab=0
ab>0
Слайд 4
Все аксиомы делятся на 5 группы:
Аксиомы откладывания
Аксиомы сложения
Аксиомы
умножения вектора на число
Аксиомы размерности
Аксиомы скалярного произведения.
Слайд 5
Контрпример к аксиоматике Вейля.
Евклидовы пространства разделяются на 2
большие группы: собственно евклидовы и псевдоевклидовы. В первых скалярный
квадрат всегда больше нуля, во вторых – может быть и отрицательный.
Мы будем рассматривать псевдоевклидово пространство, т.к. в отличие от аксиоматики Вейля там не выполняется аксиома о скалярном квадрате.
Слайд 6
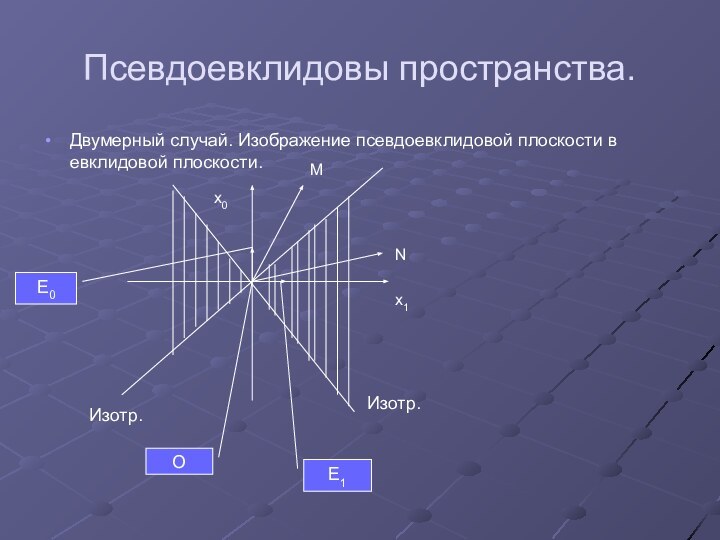
Псевдоевклидовы пространства.
Двумерный случай. Изображение псевдоевклидовой плоскости в евклидовой
плоскости.
Изотр.
Изотр.
x0
x1
M
N
O
E1
E0
Слайд 7
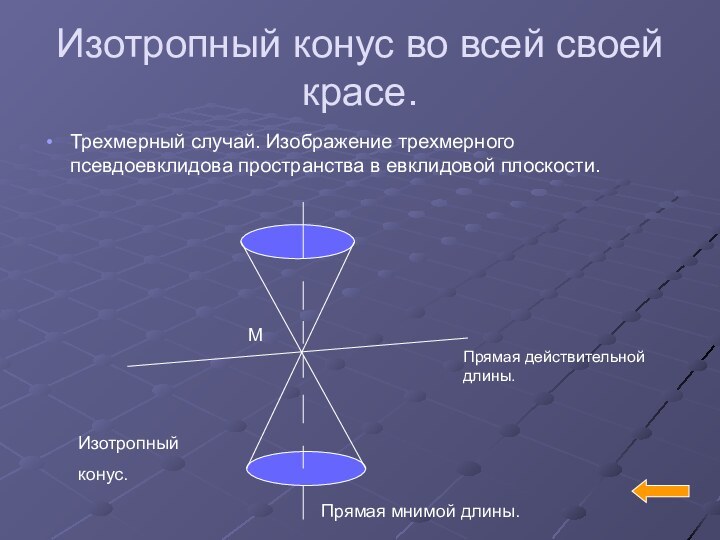
Изотропный конус во всей своей красе.
Трехмерный случай. Изображение
трехмерного псевдоевклидова пространства в евклидовой плоскости.
Изотропный
конус.
Прямая действительной длины.
Прямая мнимой
длины.
М
Слайд 8
Аксиоматика евклидовой планиметрии Гильберта.
Давид Гильберт усовершенствовал аксиоматику
самого Евклида и предоставил окончательный и совершенный ее вариант.
Основные
неопределяемые понятия: точки, прямые и плоскости. Эти объекты находятся между собой в отношениях, выражаемых словами «лежат», «между», «равны».
Множество всех прямых, точек и плоскостей называется пространством.
Слайд 9
Аксиоматика евклидовой планиметрии Гильберта.
Все аксиомы делятся на 5
групп:
Аксиомы связи (8 аксиом)
Аксиомы порядка (4 аксиомы)
Аксиомы конгруэнтности (5
аксиом)
Аксиомы непрерывности (3 аксиомы)
Аксиома параллельности (1 аксиома).
Слайд 10
Контрпример к аксиоматике Гильберта.
Для построения контрпримера мы выберем
аксиому параллельности. Рассмотрим такую геометрию, в которой выполнены все
аксиомы связи, порядка, конгруэнтности и непрерывности. Получим тогда известную геометрию Лобачевского. Рассмотрим модели этой геометрии на евклидовой плоскости.
Модель Кэли-Клейна.
Г
Точки – обычные точки внутри окружности Г, прямые – хорды этой окружности.
Окружность Г – это абсолют. Ее точки не являются точками плоскости Лобачевского.
Слайд 11
Удивительная геометрия.
Рассмотрим теперь модель Бельтрами-Пуанкаре.
Точки – обычные точки,
лежащие внутри окружности Г (абсолюта), прямые – дуги окружностей,
перпендикулярные абсолюту, а также диаметры окружности Г («окружности бесконечно большого радиуса»).
Г
Слайд 12
Еще одна модель.
Модель Пуанкаре.
Здесь точки – обычные точки,
лежащие в верхней полуплоскости по отношению к горизонтальной прямой
Г (абсолюту) и полуокружности с центром на абсолюте.
Г
Слайд 13
Многомерное евклидово пространство.
В многомерном евклидовом пространстве выполняются все
аксиомы трехмерной геометрии, за исключением одной: аксиомы о пересекающихся
плоскостях. Если в евклидовом пространстве выполняется такая аксиома: две пересекающиеся плоскости имеют единственную общую точку, - то пространство как минимум 4-мерно.
Слайд 14
Аксиоматика линейного пространства.
Непустое множество L называется линейным, или
векторным, или аффинным пространством, если:
Для любых x, yL существует
элемент x+yL, называемый их суммой.
Для любых а и xL существует элемент аxL, называемый произведением х на число a.
Элементы L называются векторами.
Слайд 15
Аксиоматика линейного пространства.
Аксиомы сложения:
x+y=y+x
x+(y+z)=(x+y)+z
x+0=x
x+(-x)=0
Аксиомы умножения вектора на число:
a(bx)=(ab)x
1*x=x
(a+b)x=ax+bx
a(x+y)=ax+ay
Аксиома
размерности:
Существует n линейно независимых векторов, но всякие n+1 вектор
линейно зависимы.
Слайд 16
Контрпример к аксиоматике линейного пространства.
Бесконечномерное линейное пространство.
Таковым является,
например, пространство числовых последовательностей вида а=(α1, α2, …, αn,…).
Все операции над ними будем выполнять покомпонентно: если а=(α1, α2, …, αn,…) и в=(β1, β2, …, βn,…), то а+в=( α1+ β1, α2+ β2, …, αn+ βn,…); с другой стороны для любого действительного p pа=(pα1, pα2, …, pαn,…). Но в таком пространстве уже не будет максимального числа линейно независимых векторов. Примером такой системы является единичный базис е1=(1, 0, 0, …), е2=(0, 1, 0, 0, …), е3=(0, 0, 1, 0, 0, …) и т.д.
Слайд 17
Гильбертово пространство.
Его абстрактное определение: это произвольное бесконечномерное линейное
пространство, в котором для любых x, y из этого
пространства задана функция (x, y), называемая скалярным произведением и обладающая следующими свойствами:
(x, x)≥0 и (x, x)=0 в том и только в том случае, если x=0;
(x+y, z)=(x, z)+(y, z);
(λx, y)=λ(x, y) для любого комплексного числа λ;
(x, y)=
Черта над формулой означает действие комплексного сопряжения.
Слайд 18
Линейные алгебры.
Непустое множество элементов называется кольцом, если в
нем определены две операции – сложение и умножение, обладающие
свойствами:
a+b=b+a (коммутативность);
a+ (b+c)=(a+b) +c (ассоциативность);
c(a+b) = ca+cb; (a+b)c=ac+bc (левая и правая дистрибутивность);
для любого a a+0=0+a=a ( существование нуля);
a+(-a)=0 для любого a (существование противоположного элемента).
Если в кольце для любых a и b справедливо ab=ba, то кольцо называют коммутативным. Если в кольце для любых a, b и c справедливо (ab)c= a(bc), то кольцо называется ассоциативным. Простейшими примерами ассоциативных и коммутативных колец являются множество целых чисел и множество четных чисел.
Слайд 19
Линейные алгебры.
Множество элементов называется полем, если это множество
состоит на менее, чем из двух элементов, является коммутативным
и ассоциативным кольцом, и если в нем существует единица поля e, обладающая свойствами:
1. ae=a;
2. aa-1=e (существование обратного элемента) a≠0.
Примерами полей могут служить поля рациональных, действительных и комплексных чисел.
Алгеброй ( или линейной алгеброй) над полем P называется пара, состоящая из кольца (A, +, ) и векторного пространства А над Р (базисное множество А у кольца и векторного пространства одно и то же; одинаковы также операция сложения + и нулевой элемент 0). Алгебра называется ассоциативной, если ассоциативно кольцо (A, +, ).
Слайд 20
Неассоциативные алгебры.
Пусть А – любая, т.е. необязательно ассоциативная
алгебра произвольной размерности над полем Р. Каждым трем элементам
x,y,z А поставим в соответствие выражение (x,y,z) =(xy) z – x (yz), называемое их ассоциатором. В зависимости от тождественных соотношений, связывающих ассоциаторы или иные выражения, получаются различные типы (как еще говорят, примитивные классы, многообразия) алгебр. Примерами служат:
1. ассоциативные алгебры: (x,y,z)=0
2. эластичные алгебры: (x,y,x)=0
3. альтернативные алгебры: (x,x,y)=(y,x,x)=0
4. йордановы алгебры: (x,y, x2)=0; xy-yx=0.
По этому аксиоматическому пути можно, очевидно, двигаться неограниченно. Рассмотрим теперь интересный пример неассоциативной алгебры – алгебра Ли.
В алгебре Ли L над полем Р произведение элементов x и y L принято обозначать [xy]. Операция (x,y) [xy] удовлетворяет двум требованиям:
1. [xx]=0 ([xy]= -[yx] - антикоммутативность);
2. [[xy] z] + [[yz] x] + [[zx] y] = 0 (тождество Якоби).
Слайд 21
Решётки.
Непустое множество, на котором заданы некоторые алгебраические операции,
называется универсальной алгеброй.
Универсальная алгебра с двумя бинарными операциями, удовлетворяющими
тождествам:
a+a=a
a+b=b+a
(a+b)+c=a+(b+c)
a(a+b)=a
a*a=a
a*b=b*a
(a*b)*c=a*(b*c)
a+a*b=a,
называется решеткой.
Пример решетки – это множество натуральных чисел относительно операций взятия наибольшего общего делителя и наименьшего общего кратного.
Слайд 22
Еще кое-что о решетках.
Два основных класса решёток –
это дистрибутивные и дедекиндовы решетки. В дистрибутивных решетках выполняется
обычный закон дистрибутивности, в дедекиндовых – заменяется на закон модулярности: если a≤c, то (a+b)c=a+bc.
Если ввести на этих типах решеток нуль и единицу с их обычными свойствами, то получим линейное пространство. При этом дедекиндова решетка будет являться контрпримером к классическому случаю линейных пространств. Произвольная решетка может и не являться линейным пространством.
Слайд 23
Аксиоматика метрического пространства.
Метрическим пространством называется пара (X,ρ), состоящая
из некоторого множества X элементов и расстояния, т.е. функции
ρ(x,y), удовлетворяющим следующим 6 аксиомам и определенной для любых x, yX:
1. ρ(x,y) однозначна, т. е. каждому x и y сопоставляется единственное значение ρ(x,y).
2. ρ(x,y)≥0.
3. ρ(x,y)R.
4. ρ(x, y)=0 тогда и только тогда, когда x=y.
5. ρ(x, y)= ρ(y, x) (аксиома симметрии).
6. ρ(x, z)≤ρ(x, y)+ρ(y, z) (аксиома треугольника).
Само метрическое пространство можно обозначить R=(X,ρ).
Слайд 24
Контрпример к аксиоматике метрического пространства.
Объект, являющийся контрпримером
к аксиоматике метрического пространства, можно построить, отказавшись от требования
однозначности. Воспользовавшись формулой расстояния в евклидовом пространстве ρ(x, y)=
потребуем, чтобы корень принимал как положительные, так и отрицательные значения. Получим множество X, на котором возможны как положительные, так и отрицательные расстояния. На рисунке показано, как будут взаимно располагаться отрезки положительной и отрицательной длины.
Линия полож. расстояний
Линия отр. расстояний
Слайд 25
Аксиоматика топологического пространства.
Пусть дано множество X. Дадим сначала
несколько определений. Окрестностью точки называется любой интервал, содержащий ее.
Точка называется предельной точкой множества, если к ней сходится некоторая последовательность точек xn. Замкнутым называется множество, содержащее все свои предельные точки. Открытым называется множество, не содержащее предельных точек дополнительного к нему множества.
Слайд 26
Как ввести топологию на множестве.
Точка прикосновения – точка

множества Х в топологическом пространстве Т – такая, что
всякая ее окрестность имеет непустое пересечение с Х. Совокупность точек прикосновения образует замыкание множества Х, это пересечение всех замкнутых множеств, содержащих Х. Обозначение [X] или Cl Х.
[X][Y]=[XY]
[X]X
[]=
[[X]]=[X]
[T]=T; XY [X][Y]
Замыкание определяет в Т топологическую структуру, в которой замкнутыми множествами считаются такие, что [X]=X.
Внутренняя точка – точка х множества Х, рассматриваемого как топологическое пространство, имеющая открытую окрестность, содержащуюся в Х. Совокупность внутренних точек образует внутренность множества Х; это – объединение всех открытых множеств, содержащихся в Х. Обозначение X или Int X.
На множествах пространства Т внутренность удовлетворяет следующим аксиомам:
XYXY
XX
TT
XX
; XY XY
Внутренность определяет в Т топологическую структуру, в которой открытыми множествами считаются такие, что X=X; эта операция двойственна операции замыкания.
Слайд 27
Аксиомы счетности.
1-ая аксиома счетности: система окрестностей
каждой точки топологического пространства Х обладает счетной базой
2-ая аксиома
счетности: система открытых множеств в Х обладает счетной базой.
Слайд 28
Контрпример к аксиоматике топологического пространства.
Произвольно взятое сепарабельное пространство
может не удовлетворять 2-ой аксиоме счетности. Поэтому контрпримером будет
именно сепарабельное пространство, поскольку в нем может не выполняться одна из основных аксиом топологического пространства.
Слайд 29
Аксиоматика натуральных чисел Пеано.
Натуральными числами называются элементы всякого
непустого множества N, где существует отношение «следует за» (число,
следующее за а обозначим через а*), удовлетворяющее аксиомам:
1. Существует число 1, не следующее ни за каким числом.
2. Для любого а существует следующее за ним число а*, и притом только одно, т.е. из а=в вытекает а*=в*.
3. Любое число следует не более чем за одним число, т.е. равенство а*=в* влечет а=в.
4. (Аксиома индукции). Пусть некоторое множество М натуральных чисел обладает свойствами:
а. 1 принадлежит М
б. Если а принадлежит М, то а*=а+1 также принадлежит М.
Тогда М содержит все натуральные числа, т.е. множество М совпадает со множеством натуральных чисел.
5. (Аксиома Архимеда). Для любых а, в, принадлежащих N, существует c, принадлежащее N, такое, что вс>a.
Слайд 30
Контрпример к аксиоматике натуральных чисел.
Неиндуктивные системы счисления.
Графическая модель
такой системы представлена на рисунке ниже.
либо
1
2
3
4
n-1
n
n+1
n+2 …
n+3
n+3
n+4
n+5 …
Аксиома
индукции выполняется для чисел, находящихся на прямой, но не выполняются для чисел, представленных точками, лежащими на окружности или другой прямой, т.к. нарушено условие следования чисел, содержащееся в аксиоме индукции.
Слайд 32
Выводы.
Таким образом, мы построили контрпример к каждой аксиоматической
системе. Мы исследовали свойства построенных нами объектов. Значит, можно
сделать вывод, что независимость аксиом в данных аксиоматических системах имеет место. Наша гипотеза оправдалась. Значит, эти системы аксиом являются правильно сформулированными.