- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме Введение в теорию вероятностей
Содержание
- 2. I. ОсновоположникиXVII век Б. Паскаль, П. Ферма, Х. ГюйгенсБ.Паскаль(1623 – 1662)П.Ферма1601-1665Х.Гюйгенс(1629 – 1695)
- 3. Элементарные события (исходы) – простейшие события, которыми
- 4. III. Решение задачЗадача 1.Вася, Петя, Коля и
- 5. Задача 2.Какова вероятность того, что случайно выбранное
- 6. Задача 3.Перед началом футбольного матча судья бросает
- 7. Задача 4.Игральный кубик бросили один раз. Какова
- 8. Задача 5. В случайном эксперименте симметричную монету
- 9. Задача 6.Монету бросают дважды. Найдите вероятность того,
- 10. Задача 7. В случайном эксперименте бросают два
- 11. Задача 8.Игральный кубик бросают дважды. Найдите вероятность
- 12. Задача 9.Игральный кубик бросают дважды. Найдите вероятность
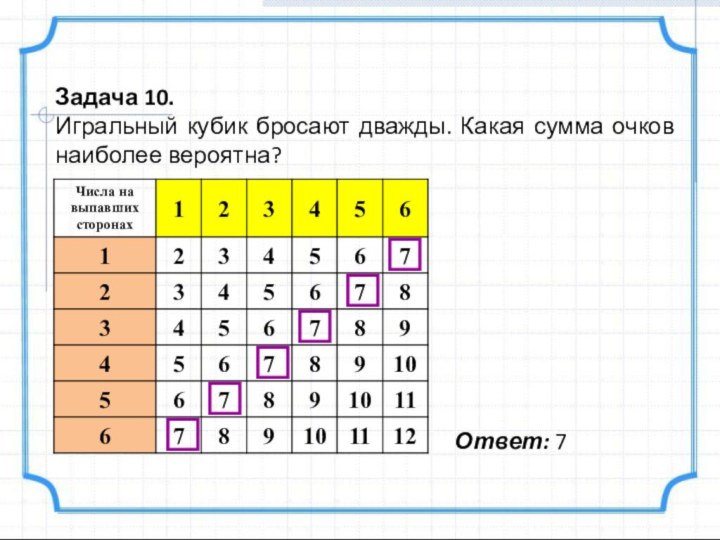
- 13. Задача 10.Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна?Ответ: 7
- 14. Задача 11. В случайном эксперименте монету бросили
- 15. Задача 12.Монету бросают три раза. Какова вероятность
- 16. Задача 13.Монету бросают четыре раза. Найдите вероятность
- 17. Задача 14. В соревнованиях по толканию ядра
- 18. Задача 15. В среднем из 1000 аккумуляторов,
- 19. Задача 16. В чемпионате по гимнастике участвуют
- 20. Задача 17.В некотором городе из 5000 появившихся
- 21. Задача 18. Вероятность того, что шариковая ручка
- 22. Задача 19.На экзамене по геометрии школьнику достается
- 23. А={кофе закончится в первом автомате}B={кофе закончится во
- 24. Скачать презентацию
- 25. Похожие презентации













![Презентация по теме Введение в теорию вероятностей Домашнее заданиеМАОУ Лицей ИГУ г. Иркутска, ligu.edu38.ru*КонспектСР «Введение в ТВ»«16_[ДЗ]Введение в ТВ.doc»](/img/tmb/7/664503/fa3e4b5868bfa6c7e78638422fd33d3f-720x.jpg)
Слайд 2
I. Основоположники
XVII век
Б. Паскаль, П. Ферма, Х. Гюйгенс
Б.Паскаль
(1623 – 1662)
П.Ферма
1601-1665
Х.Гюйгенс
(1629
– 1695)
Слайд 3
Элементарные события (исходы) –
простейшие события, которыми может
окончится случайный опыт
Обозначение: A, B, C, D, …
Классическое определение
вероятности:Вероятностью события А называется отношение числа m элементарных исходов, благоприятствующих этому событию, к общему числу элементарных исходов испытания n.
Формула:
II. Основные понятия
Свойства:
1)
2) Для достоверного события m=n и P(А)=1
3) Для невозможного события m=0 и P(А)=0
Слайд 4
III. Решение задач
Задача 1.
Вася, Петя, Коля и Леша
бросили жребий – кому начинать игру. Найдите вероятность того,
что игру будет начинать Петя.Решение:
P(A) = m/n
P(A) = ¼ = 0,25
Ответ: 0,25
Дано:
n = 4
А = {жребий выиграл Петя}
m = 1
Найти:
P(A) - ?
Слайд 5
Задача 2.
Какова вероятность того, что случайно выбранное натуральное
число от 10 до 19 делится на три?
10, 11,
12, 13, 14, 15, 16, 17, 18, 19Решение:
P(A) = m/n
P(A) = 3/10 = 0,3
Ответ: 0,3
Дано:
n = 10
m = 3
Найти:
P(A) - ?
Слайд 6
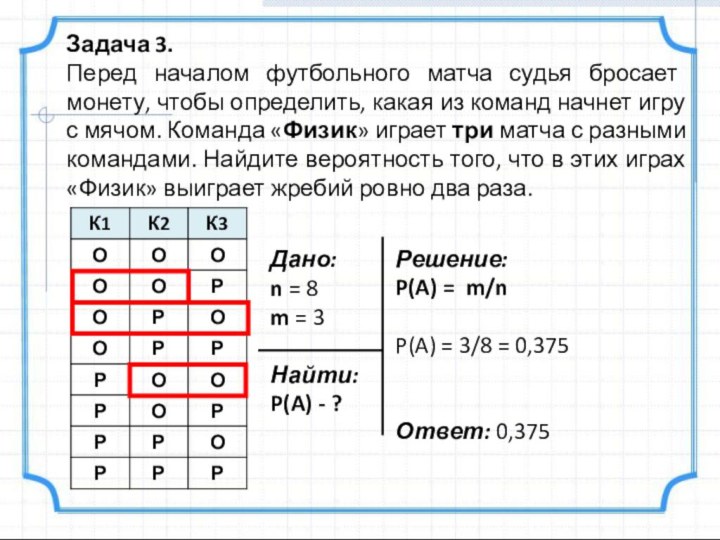
Задача 3.
Перед началом футбольного матча судья бросает монету,
чтобы определить, какая из команд начнет игру с мячом.
Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.Решение:
P(A) = m/n
P(A) = 3/8 = 0,375
Ответ: 0,375
Дано:
n = 8
m = 3
Найти:
P(A) - ?
Слайд 7
Задача 4.
Игральный кубик бросили один раз. Какова вероятность
того, что выпало число очков, большее чем 4.
Элементарные события:
1,
2, 3, 4, 5, 6Решение:
P(A) = m/n
P(A) = 2/6 = 1/3
Ответ: 1/3
Дано:
n = 6
m = 2
Найти:
P(A) - ?
Слайд 8
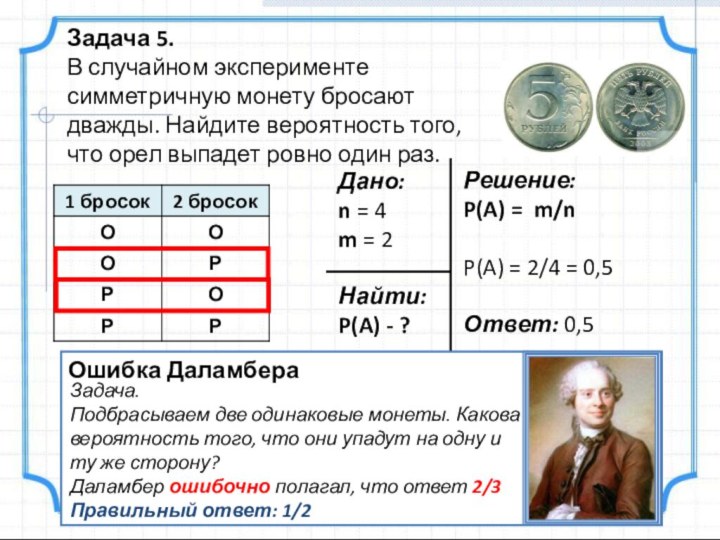
Задача 5.
В случайном эксперименте симметричную монету бросают
дважды. Найдите вероятность того, что орел выпадет ровно один
раз.Решение:
P(A) = m/n
P(A) = 2/4 = 0,5
Ответ: 0,5
Дано:
n = 4
m = 2
Найти:
P(A) - ?
Ошибка Даламбера
Задача.
Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону?
Даламбер ошибочно полагал, что ответ 2/3
Правильный ответ: 1/2
Слайд 9
Задача 6.
Монету бросают дважды. Найдите вероятность того, что
выпадет хотя бы один ОРЕЛ.
Решение:
P(A) = m/n
P(A) = 3/4
= 0,75Ответ: 0,75
Дано:
n = 4
m = 3
Найти:
P(A) - ?
Слайд 10
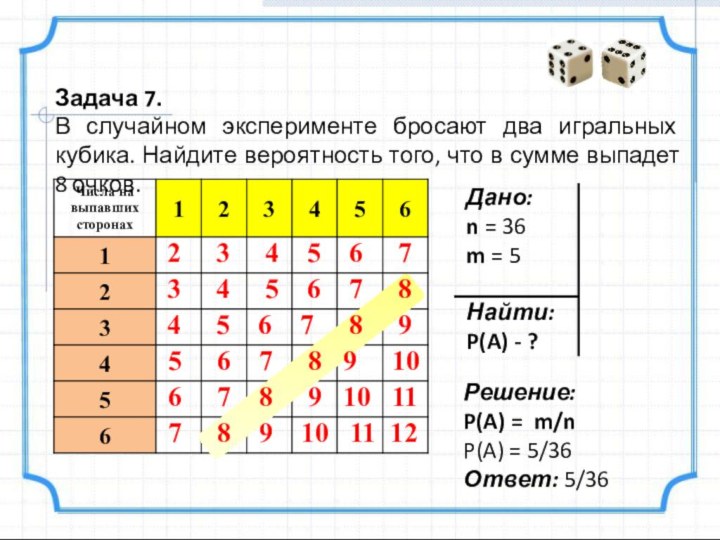
Задача 7.
В случайном эксперименте бросают два игральных
кубика. Найдите вероятность того, что в сумме выпадет 8
очков.2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
5 6 7 8 9 10
6 7 8 9 10 11
7 8 9 10 11 12
Решение:
P(A) = m/n
P(A) = 5/36
Ответ: 5/36
Дано:
n = 36
m = 5
Найти:
P(A) - ?
Слайд 11
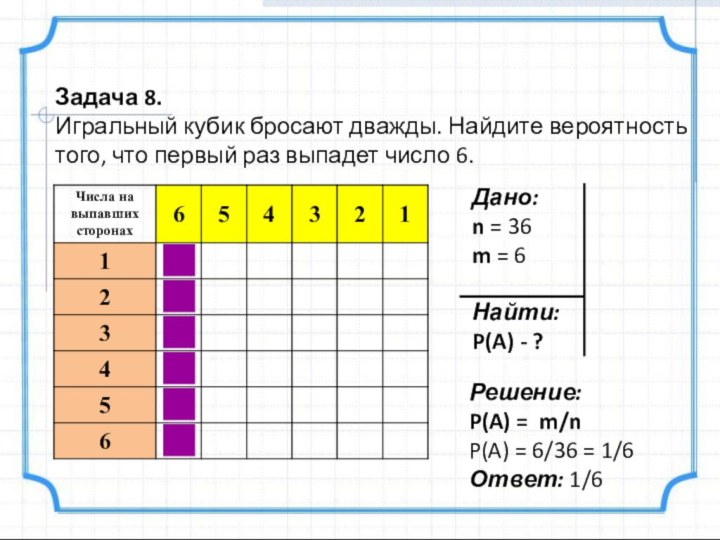
Задача 8.
Игральный кубик бросают дважды. Найдите вероятность того,
что первый раз выпадет число 6.
Решение:
P(A) = m/n
P(A) =
6/36 = 1/6Ответ: 1/6
Дано:
n = 36
m = 6
Найти:
P(A) - ?
Слайд 12
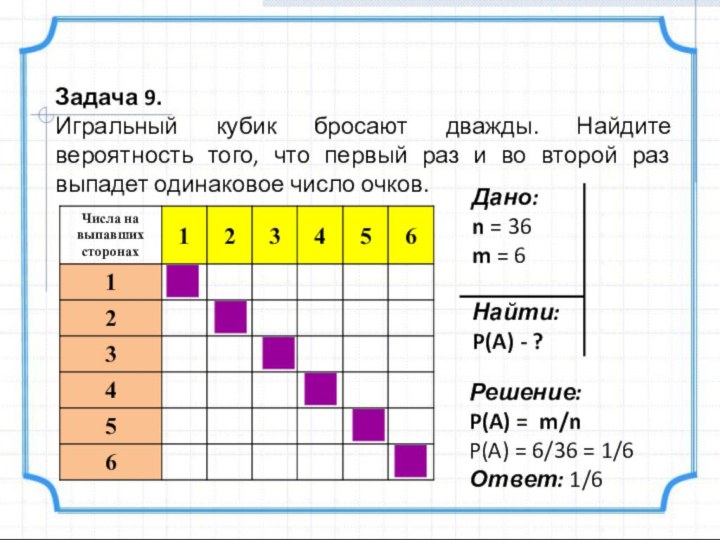
Задача 9.
Игральный кубик бросают дважды. Найдите вероятность того,
что первый раз и во второй раз выпадет одинаковое
число очков.Решение:
P(A) = m/n
P(A) = 6/36 = 1/6
Ответ: 1/6
Дано:
n = 36
m = 6
Найти:
P(A) - ?
Слайд 14
Задача 11.
В случайном эксперименте монету бросили три
раза. Какова вероятность того, что орел выпал ровно два
раза.Решение:
P(A) = m/n
P(A) = 3/8 = 0,375
Ответ: 0,375
Дано:
n = 8
m = 3
Найти:
P(A) - ?
Слайд 15
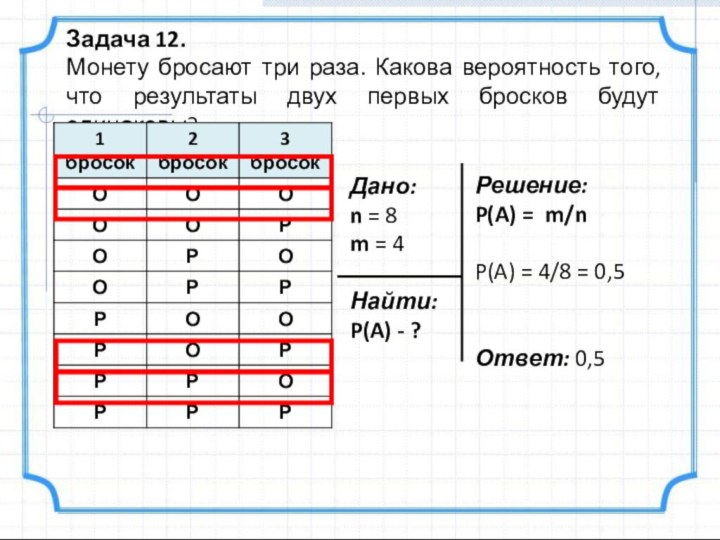
Задача 12.
Монету бросают три раза. Какова вероятность того,
что результаты двух первых бросков будут одинаковы?
Решение:
P(A) = m/n
P(A)
= 4/8 = 0,5Ответ: 0,5
Дано:
n = 8
m = 4
Найти:
P(A) - ?
Слайд 16
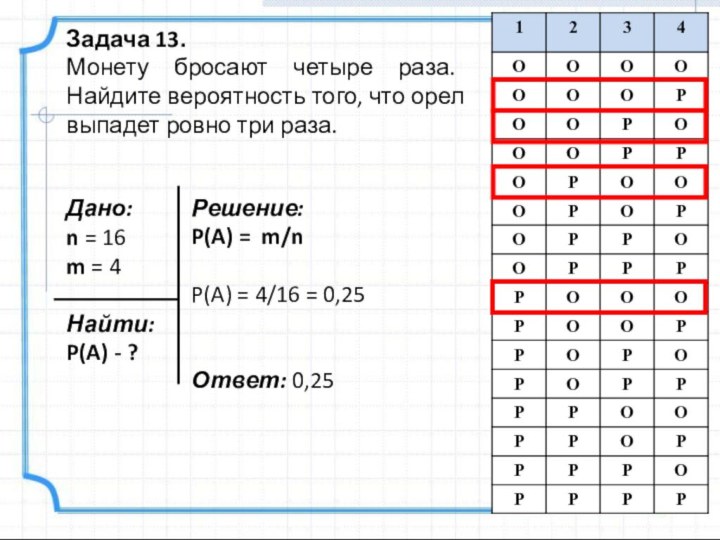
Задача 13.
Монету бросают четыре раза. Найдите вероятность того,
что орел выпадет ровно три раза.
Решение:
P(A) = m/n
P(A) =
4/16 = 0,25Ответ: 0,25
Дано:
n = 16
m = 4
Найти:
P(A) - ?
Слайд 17
Задача 14.
В соревнованиях по толканию ядра участвуют
4 спортсмена из Финляндии, 7 спортсменов из Дании, 9
спортсменов из Швеции и 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.Решение:
P(A) = m/n
P(A) = 9/25 = 0,36
Ответ: 0,36
Дано:
n = 4 + 7 + 9 + 5 = 25
m = 9
Найти:
P(A) - ?
Слайд 18
Задача 15.
В среднем из 1000 аккумуляторов, поступивших
в продажу, 6 неисправны. Найдите вероятность того, что купленный
аккумулятор окажется исправным.Решение:
P(A) = m/n
P(A) = 994/1000 = 0,994
Ответ: 0,994
Дано:
n = 1000
m = 1000 – 6 = 994
Найти:
P(A) - ?
Слайд 19
Задача 16.
В чемпионате по гимнастике участвуют 20
спортсменок: 8 из России, 7 из США , остальные
из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.Решение:
P(A) = m/n
P(A) = 5/20 = 0,25
Ответ: 0,25
Дано:
n = 20
m = 20 – (8 + 7) = 5
Найти:
P(A) - ?
Слайд 20
Задача 17.
В некотором городе из 5000 появившихся на
свет младенцев оказалось 2512 мальчиков. Найдите частоту рождения девочек
в этом городе. Результат округлите до тысячных.Решение:
P(A) = m/n
P(A) = 2488/5000 = 0,4976
≈ 0, 498
Ответ: 0,498
Дано:
n = 5000
m = 5000 – 2512
= 2488
Найти:
P(A) - ?
Слайд 21
Задача 18.
Вероятность того, что шариковая ручка пишет
плохо (или не пишет) равна 0,1. Покупатель в магазине
выбирает одну такую ручку. Найдите вероятность того, что ручка пишет хорошо.Решение:
A={ручка пишет хорошо}
Противоположное событие:
Ответ: 0,9
Слайд 22
Задача 19.
На экзамене по геометрии школьнику достается один
вопрос из списка экзаменационных вопросов. Вероятность того, что это
вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.Решение:
А={вопрос на тему «Вписанная окружность»}
B={вопрос на тему «Параллелограмм»}
События А и В несовместны, т.к. нет вопросов относящихся к двум темам одновременно
С={вопрос по одной из этих тем}
Р(С)=Р(А) + Р(В)
Р(С)=0,2 + 0,15=0,35
Ответ: 0,35