- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Медиана треугольника
Содержание
- 2. Цели урока:Дать определение медианы треугольникаСформулировать основное свойство
- 3. Определение:Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой
- 4. Основное свойствоВсе три медианы треугольника пересекаются в
- 5. Теорема (Свойство медианы равнобедренного треугольника)В равнобедренном треугольнике
- 6. Другие свойства Медиана разбивает треугольник на два равновеликих (по
- 7. Основные соотношения
- 8. Решение задач
- 9. Решение задачВ треугольнике ABC стороны AB, BC
- 10. Домашнее заданиеУчебник: Л. С. Атанасян «Геометрия 7-9» №106, 109, 114
- 11. Скачать презентацию
- 12. Похожие презентации
Цели урока:Дать определение медианы треугольникаСформулировать основное свойство медианыСформулировать и доказать теорему о свойстве медианы равнобедренного треугольникаДругие свойстваЗаписать основные соотношения для медианы и решить задачи с применением этих формул









Слайд 2
Цели урока:
Дать определение медианы треугольника
Сформулировать основное свойство медианы
Сформулировать
и доказать теорему о свойстве медианы равнобедренного треугольника
основные соотношения для медианы и решить задачи с применением этих формул
Слайд 3
Определение:
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной
стороны. Точка пересечения медианы со стороной треугольника называется основанием медианы.
А
В
С
Слайд 4
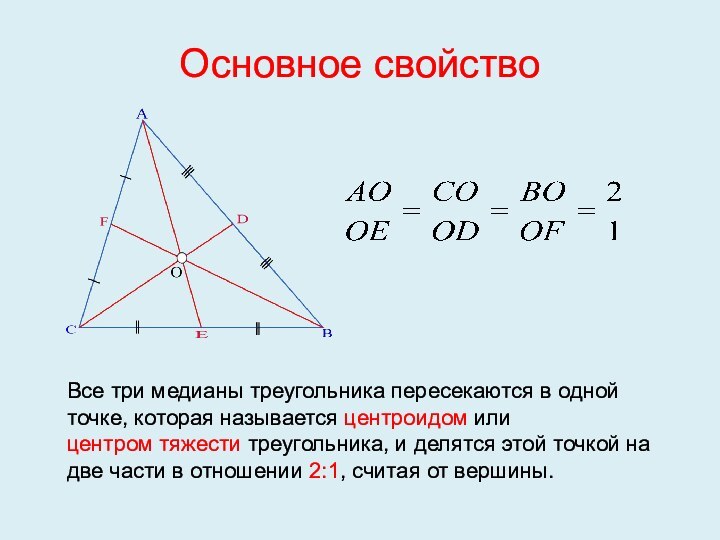
Основное свойство
Все три медианы треугольника пересекаются в одной
точке, которая называется центроидом или
центром тяжести треугольника, и делятся этой точкой
на две части в отношении 2:1, считая от вершины.
Слайд 5
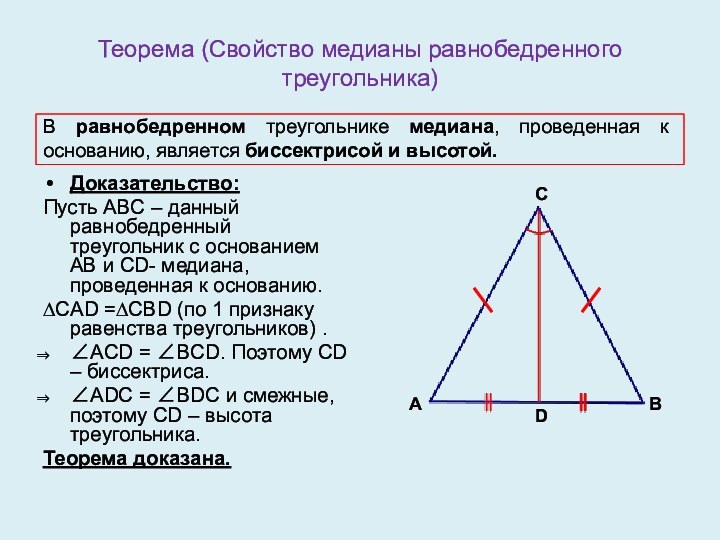
Теорема (Свойство медианы равнобедренного треугольника)
В равнобедренном треугольнике медиана,
проведенная к основанию, является биссектрисой и высотой.
Доказательство:
Пусть ABC –
данный равнобедренный треугольник с основанием AB и CD- медиана, проведенная к основанию.∆CAD =∆CBD (по 1 признаку равенства треугольников) .
∠ACD = ∠BCD. Поэтому CD – биссектриса.
∠ADC = ∠BDC и смежные, поэтому CD – высота треугольника.
Теорема доказана.
C
A
B
D
Слайд 6
Другие свойства
Медиана разбивает треугольник на два равновеликих (по площади)
треугольника.
Треугольник делится тремя медианами на шесть равновеликих треугольников.
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.Большей стороне треугольника
соответствует меньшая медиана.
Слайд 9
Решение задач
В треугольнике ABC стороны AB, BC и
CA равны соответственно 4, 5, 7.
Найти
все медианы треугольника.Известно, что в треугольнике abc медиана m_a = ,
m_b = , m_c = .
Найти стороны треугольника.
Ответ:
1 вариант
2 вариант
Ответ: a = 4,
b = 6,
c = 7





























