- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Стереометрические задания в ЕГЭ по математике
Содержание
- 2. В математике есть своя красота, как в живописи и поэзии. (Н.Е.Жуковский)
- 3. Задание С2 Единого государственного экзамена вот уже
- 4. Основные проблемы: неумение строить линейные углы и
- 5. Модели или чертежи многогранников, обладающие конкретностью и
- 6. Повторение:Двугранный угол, образованный полуплоскостями измеряется величиной его
- 7. . - АСВперпендикулярнаклоннаяпроекцияУгол ВMN – линейный угол
- 8. . - DАВСА1D1С1В1перпендикулярнаклоннаяУстно:Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.№ 2
- 9. . - DАВСА1D1С1В1Устно:Дан куб. Покажите следующие двугранные
- 10. . - В прямоугольном параллелепипеде АВСДА1В1С1Д1, у
- 11. . - αПовторение:АРасстояние от точки до плоскости,
- 12. . - В единичном кубе АВСДА1В1С1Д1 найдите
- 13. Литература1)А.Г. Корянов, А.А. ПрокофьевЛекции 5 Готовим к
- 14. Скачать презентацию
- 15. Похожие презентации
В математике есть своя красота, как в живописи и поэзии. (Н.Е.Жуковский)









Слайд 3
Задание С2 Единого государственного экзамена вот уже два
года представляло стереометрическую задачу на определение расстояний или углов
в пространстве между объектами, связанными с некоторым многогранником.Решение задания С2 оценивается 2 баллами. Один бал начисляется за правильное построение или описание искомого угла или расстояния. Еще один бал начислялся за правильно проведенные вычисления и верный ответ.
Слайд 4
Основные проблемы: неумение строить линейные углы и проекции,
ошибки в определении вида треугольника, вычислительные ошибки. Многие выпускники
демонстрировали
непонимание нахождения угла между прямой и плоскостью. При решении заданий выпускники показали недостаточное представление о расположении перпендикуляра при нахождении расстояния от точки до прямой. Все отмеченное указывает на то, что учащиеся испытывают большие трудности при решении стереометрических задач. В отличие от планиметрии в стереометрии они не могут опереться на наглядность. Выходом из этого
положения является использование чертежей многогранников, на которых можно показать все теоремы стереометрии.
Слайд 5
Модели или чертежи многогранников, обладающие конкретностью и содержательностью,
являются инструментом для развития пространственного воображения школьников и успешного
изучения стереометрии. По принципу «от простого — к сложному» следует рассматривать решения задач, придерживаясь такой последовательности многогранников: куб, правильная призма (треугольная, четырехугольная, шестиугольная), прямая призма, правильный тетраэдр, правильная пирамида (треугольная, четырехугольная, шестиугольная).
Слайд 6
Повторение:
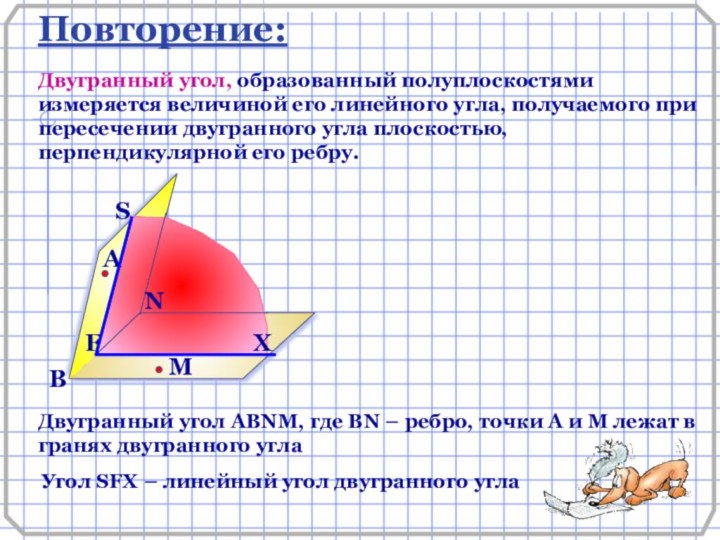
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного
угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его
ребру.А
В
N
М
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла
Угол SFX – линейный угол двугранного угла
Слайд 7
.
-
А
С
В
перпендикуляр
наклонная
проекция
Угол ВMN – линейный угол двугранного
угла ВАСК
К
Устно:
Построить линейный угол двугранного
угла ВАСК.
Треугольник АВС –
равнобедренный.№ 1
Слайд 8
.
-
D
А
В
С
А1
D1
С1
В1
перпендикуляр
наклонная
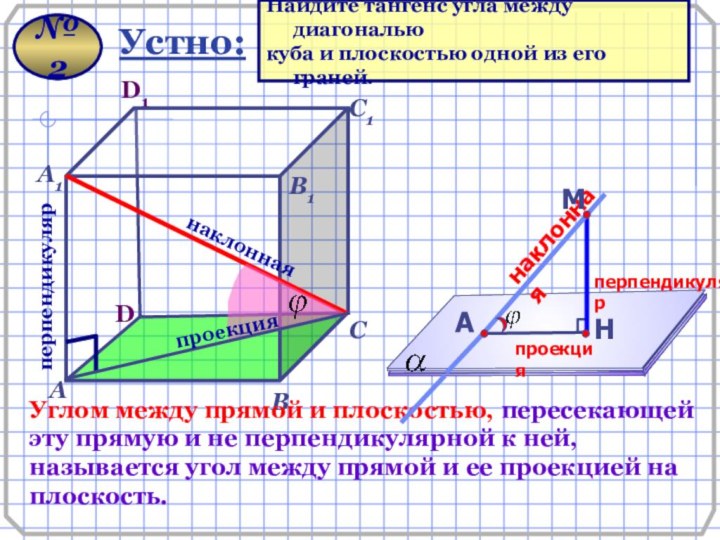
Устно:
Найдите тангенс угла между диагональю
куба
и плоскостью одной из его граней.
№ 2
Слайд 9
.
-
D
А
В
С
А1
D1
С1
В1
Устно:
Дан куб. Покажите следующие
двугранные углы:
а)АВВ1С;
б) АDD1B;
в) А1ВВ1К, где К середина
ребра А1Д1№ 3
Слайд 10
.
-
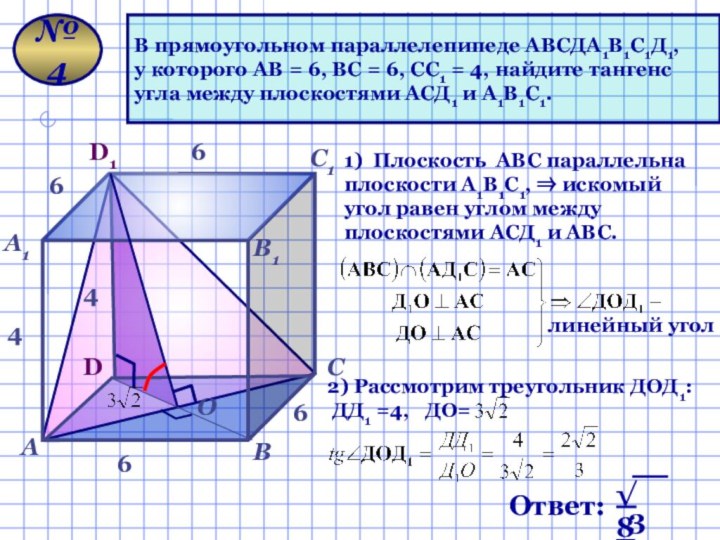
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого
АВ = 6, ВС = 6, СС1 = 4,
найдите тангенсугла между плоскостями АСД1 и А1В1С1.
№ 4
4
4
6
6
6
6
О
1) Плоскость AВС параллельна плоскости А1В1С1, ⇒ искомый угол равен углом между плоскостями АСД1 и АВС.
линейный угол
2) Рассмотрим треугольник ДОД1:
ДД1 =4, ДО=
Слайд 11
.
-
α
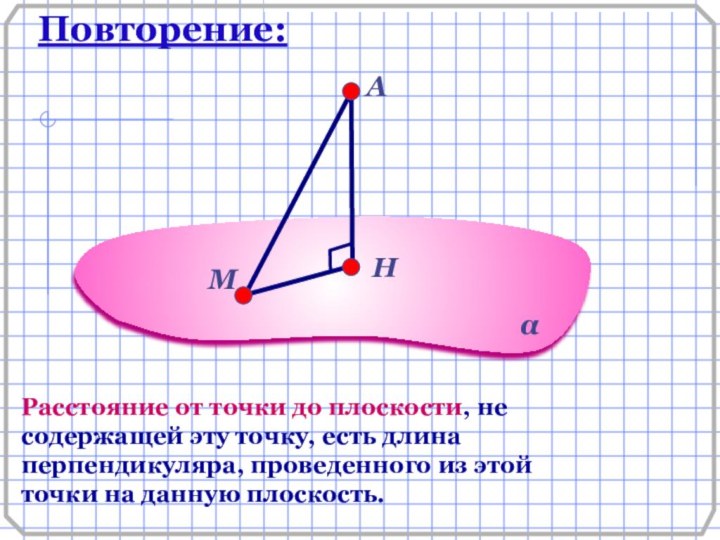
Повторение:
А
Расстояние от точки до плоскости, не
содержащей эту точку, есть длина перпендикуляра, проведенного из этой
точки на данную плоскость.Н
Слайд 12
.
-
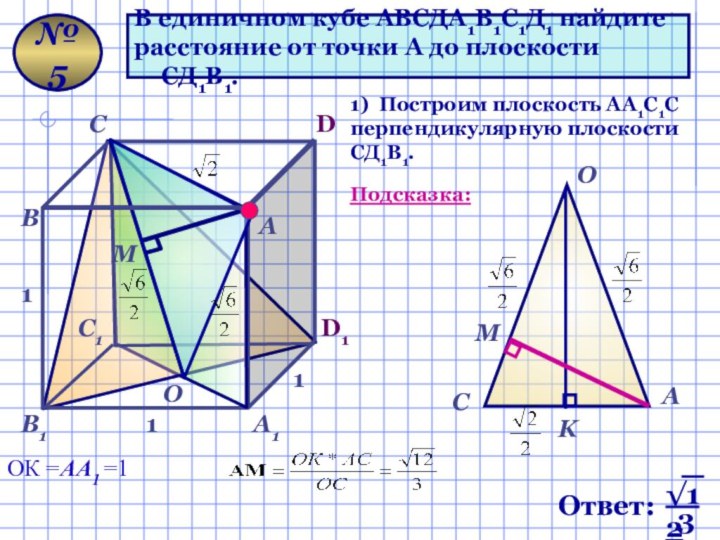
В единичном кубе АВСДА1В1С1Д1 найдите
расстояние
от точки А до плоскости СД1В1.
№ 5
1
1
1
М
О
1) Построим плоскость
AА1С1С перпендикулярную плоскости СД1В1.Подсказка:
K
ОК =АА1 =1
Слайд 13
Литература
1)А.Г. Корянов, А.А. Прокофьев
Лекции 5 Готовим к ЕГЭ
хорошистов и отличников
2)В.А. Смирнов ЕГЭ 2011. Математика. Задача С2.
Геометрия. Стереометрия. / Под. редакцией А.Л. Семенова и И.В. Ященко. – М.: МЦНМО, 2011.3) http://le-savchen.ucoz.ru/
4) http://edu.1september.ru/