Слайд 3
Эллипс
Определения и свойства:
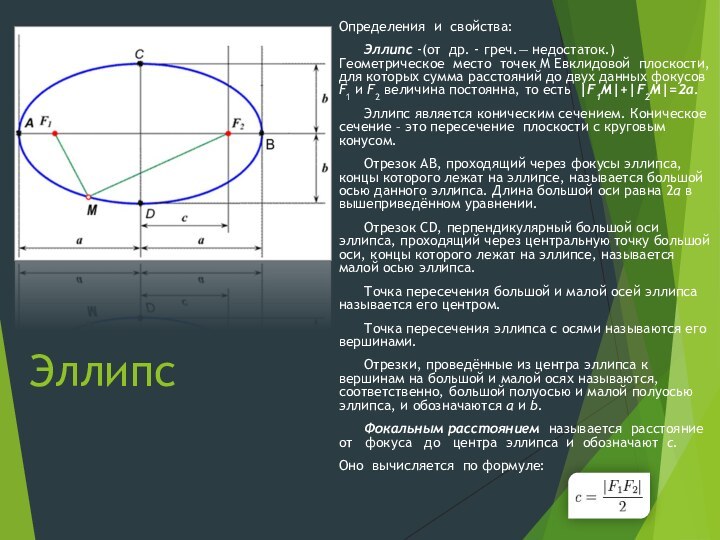
Эллипс -(от др. - греч.— недостаток.) Геометрическое место
точек M Евклидовой плоскости, для которых сумма расстояний до двух данных фокусов F1 и F2 величина постоянна, то есть |F1M|+|F2M|=2a.
Эллипс является коническим сечением. Коническое сечение – это пересечение плоскости с круговым конусом.
Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
Точка пересечения большой и малой осей эллипса называется его центром.
Точка пересечения эллипса с осями называются его вершинами.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Фокальным расстоянием называется расстояние от фокуса до центра эллипса и обозначают c.
Оно вычисляется по формуле:
Слайд 4
Эллипс
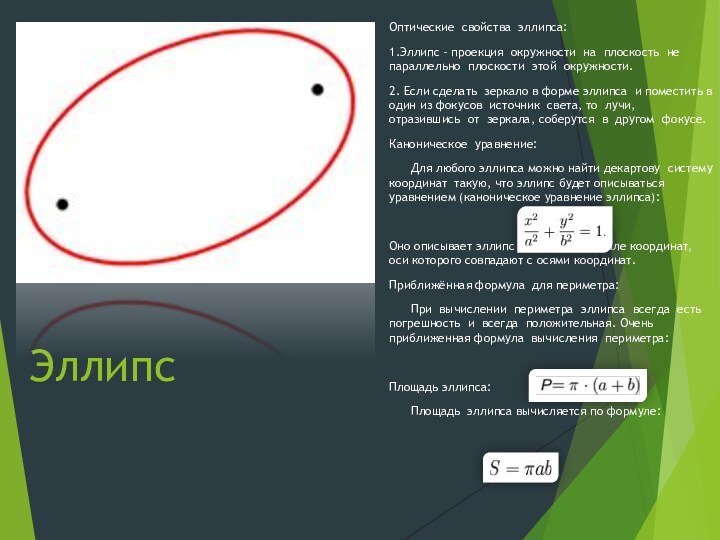
Оптические свойства эллипса:
1.Эллипс – проекция окружности на плоскость
не параллельно плоскости этой окружности.
2. Если сделать зеркало в
форме эллипса и поместить в один из фокусов источник света, то лучи, отразившись от зеркала, соберутся в другом фокусе.
Каноническое уравнение:
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.
Приближённая формула для периметра:
При вычислении периметра эллипса всегда есть погрешность и всегда положительная. Очень приближенная формула вычисления периметра:
Площадь эллипса:
Площадь эллипса вычисляется по формуле:
Слайд 5
Эллипс
Эллипсы в реальности встречаются гораздо чаще, чем, кажется.
Например, планеты солнечной системы движутся по эллиптическим орбитам, кольца
Сатурна также имеют эллиптическую форму.
В форме эллипса можно изготовить журнальный столик или соткать ковер.
А у садоводов свой способ применения эллипса: в землю втыкают два колышка, крепят веревку к колышкам (один конец к одному второй к другому), верёвку оттягивают в сторону и вычерчивают эллипс с помощью палки.
Слайд 6
Гипербола
Определение и свойства:
Гипербола (от др.
- греч. бол— «бросать», гипер— «сверх». Термин «гипербола» был
введён Аполлонием Пергским.) —геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух данных фокусов F1 и F2 постоянно, то есть
||F1M|−|F2M|| =C
Гипербола является коническим сечением.
Осью гиперболы называется прямая, соединяющая её фокусы.
Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы и обозначают с.
Каждая гипербола имеет пару асимптот: Асимптота кривой – это прямая к которой стремится ветвь кривой неограниченно приближаясь, но никогда не пересекая её.
Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы и обозначается a.
Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы и обозначается b.
Слайд 7
Гипербола
Оптические свойства:
Свет от источника, находящегося
в одном из фокусов гиперболы, отражается второй ветвью гиперболы
таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
Каноническое уравнение:
Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением:
Равнобочная гипербола:
Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением:
X*Y = a2/2
Слайд 8
ГИПЕРБОЛА
Гиперболу можно встретить везде, даже в космосе:
Траектории некоторых космических тел, проходящих вблизи звезды или другого
массивного объекта на достаточно большой скорости могут имеют форму гиперболы.
С помощью гиперболы военные определяют, как нужно направить орудие, чтобы поразить неподвижную звучащую цель, например, стреляющее орудие противника.
Слайд 9
Парабола
Определение и свойства:
Парабола - (от
греч. — приложение) —геометрическое место точек M равноудалённых от данной прямой(называемой
директрисой параболы) и данного фокуса.
Рассмотрим такие точки M на плоскости, которые равноудалены от фокуса F и от директрисы PQ (Это значит, что длина отрезка FM равна длине перпендикуляра, опущенного из точки M на директрису PQ)
Парабола является коническим сечением.
Начало координат O — середина отрезка CF.
Парабола имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе.
Все параболы подобны, а расстояние между фокусом и директрисой определяет масштаб.
Слайд 10
Парабола
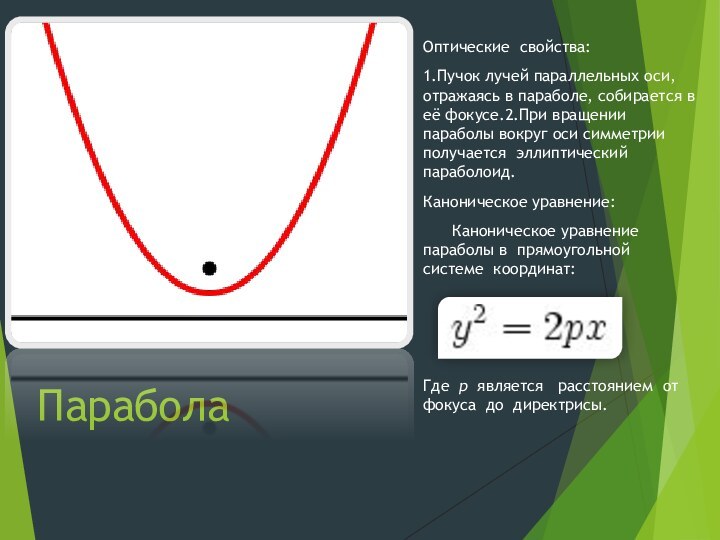
Оптические свойства:
1.Пучок лучей параллельных оси, отражаясь в параболе,
собирается в её фокусе.2.При вращении параболы вокруг оси симметрии
получается эллиптический параболоид.
Каноническое уравнение:
Каноническое уравнение параболы в прямоугольной системе координат:
Где p является расстоянием от фокуса до директрисы.