Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Быстрый счет без калькулятора

Содержание

2. Умеете ли Вы считать? Каждый, конечно скажет:
3. Хорошо ли Вы считаете? Об умении считать можно
4. ИсследованиеНайти значение выражения:34 • 1,5 + 124 • 25
5. Проблема исследования Много ошибок при выполнении вычислений, сложности при устном счёте.
6. Осново-полагающий вопросКак за короткое время научиться быстро считать, если ты обыкновенный школьник, а не вундеркинд?
7. Гипотеза Существуют специальные способы выполнения действий,
8. Цель проектаНайти и освоить нестандартные приёмы, позволяющие
9. АктуальностьАктуальность данной темы заключается в том,
10. Творческое название исследо-вательского проектаБЫСТРЫЙ СЧЁТ БЕЗ КАЛЬКУЛЯТОРА
12. «Метод решётки» Пусть нужно умножить
13. Пример: 34×5=170Как умножалиегиптяне. Т.к. 5 =
14. Умножение на 9Пальцевой счет
15. Общие приемы быстрого счетаразложение каждого слагаемого
16. Умножение на 1,5Чтобы умножить число на 1,5,
17. Умножение на 11 Чтобы умножить двузначноечисло
18. Умножение и деление на 5Чтобы число
19. Умножение на 25, на125Чтобы число
20. Возведение в квадрат числа, оканчивающегося цифрой
21. Возведение в квадрат числа, близкого к 50Хочешь
22. Умножение на 101, на 1001…Чтобы умножить
23. Умножение на 9, 99, 999,…Чтобы умножить число
24. ЗаключениеДействительно, существуют специальные способы выполнения действий, которые
25. Скачать презентацию
26. Похожие презентации

Умеете ли Вы считать? Каждый, конечно скажет: «Да!» Это очень важные умения, так как вычислительные навыки являются фундаментом изучения математики и других учебных дисциплин.

Главная
Математика
Презентация Быстрый счет без калькулятора

МБОУ « Гимназия »г. НовозыбковаБыстрый счёт без калькулятора Учитель: Арещенко Елена Александровна

Умеете ли Вы считать? Каждый, конечно скажет: «Да!» Это очень важные умения,

Хорошо ли Вы считаете? Об умении считать можно судить: - по умению производить устные

ИсследованиеНайти значение выражения:34 • 1,5 + 124 • 25

Проблема исследования Много ошибок при выполнении вычислений, сложности при устном счёте.

Осново-полагающий вопросКак за короткое время научиться быстро считать, если ты обыкновенный школьник, а не вундеркинд?

Гипотеза Существуют специальные способы выполнения действий, которые позволяют свести вычисления к

Цель проектаНайти и освоить нестандартные приёмы, позволяющие выполнить действия с числами быстро

АктуальностьАктуальность данной темы заключается в том, что использование нестандартных приемов вычислений

Творческое название исследо-вательского проектаБЫСТРЫЙ СЧЁТ БЕЗ КАЛЬКУЛЯТОРА

«Метод решётки» Пусть нужно умножить 25 и 63.

Пример: 34×5=170Как умножалиегиптяне. Т.к. 5 = 4 + 1, то для

Общие приемы быстрого счетаразложение каждого слагаемого на разряды;использование переместительного и сочетательного

Умножение на 1,5Чтобы умножить число на 1,5, нужно к исходному числу прибавить

Умножение на 11 Чтобы умножить двузначноечисло на 11, надо цифры этогочисла

Умножение и деление на 5Чтобы число умножить на 5, нужно умножить

Умножение на 25, на125Чтобы число умножить на 25, нужно разделить

Возведение в квадрат числа, оканчивающегося цифрой 5Чтобы возвести в квадрат число,оканчивающееся

Возведение в квадрат числа, близкого к 50Хочешь возвести в квадрат число, близкое

Умножение на 101, на 1001…Чтобы умножить число на 101, нужно приписать

Умножение на 9, 99, 999,…Чтобы умножить число на 9, к нему приписывают

ЗаключениеДействительно, существуют специальные способы выполнения действий, которые позволяют свести вычисления к устным,

Слайды презентации

Слайд 2 Умеете ли Вы считать?
Каждый, конечно скажет: «Да!»

Это

Умеете ли Вы считать? Каждый, конечно скажет: «Да!» Это очень важные

очень важные умения, так как вычислительные навыки являются

фундаментом
изучения математики и других
учебных дисциплин.

Но сегодня особо ценится умение не только правильно,
но и быстро считать.

Слайд 3 Хорошо ли Вы считаете?

Об умении считать можно судить:
-

Хорошо ли Вы считаете? Об умении считать можно судить: - по умению производить

по умению производить устные и письменные вычисления,
- по рациональной

организации хода вычисления,
- по умению убеждаться в правильности полученных результатов.

Качество вычислительных умений определяется двумя вещами:
знанием правил;
знанием алгоритмов вычислений.

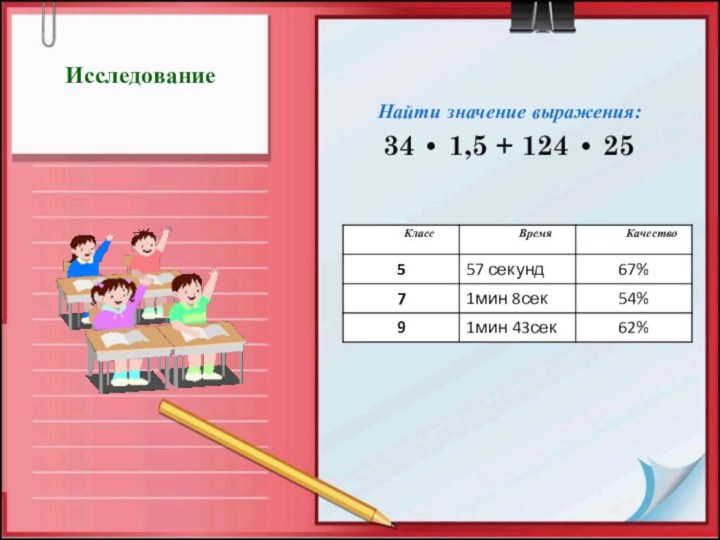
Слайд 4 Исследование
Найти значение выражения:
34 • 1,5 + 124 •

25

Слайд 5 Проблема исследования
Много ошибок при выполнении вычислений, сложности

при устном счёте.

Слайд 6 Осново-полагающий вопрос
Как за короткое время научиться быстро считать,

если ты обыкновенный школьник,
а не вундеркинд?

Слайд 7 Гипотеза
Существуют специальные способы выполнения действий, которые позволяют

Гипотеза Существуют специальные способы выполнения действий, которые позволяют свести вычисления

свести вычисления к устным, рассчитанные на ум «обычного» человека

и не требующие уникальных способностей.

Главное – небольшая тренировка.

Слайд 8 Цель проекта
Найти и освоить нестандартные приёмы, позволяющие выполнить

Цель проектаНайти и освоить нестандартные приёмы, позволяющие выполнить действия с числами

действия с числами быстро (устно) и безошибочно.

Создать справочник,

в котором разместить информацию о наиболее полезных для школьников приёмах быстрого счёта.

Слайд 9 Актуальность
Актуальность данной темы заключается в том, что использование

АктуальностьАктуальность данной темы заключается в том, что использование нестандартных приемов

нестандартных приемов вычислений усиливает интерес учащихся к математике и

содействует развитию математических способностей, внимания, памяти, экономит время решения заданий.

Слайд 10 Творческое название исследо-вательского проекта
БЫСТРЫЙ СЧЁТ БЕЗ КАЛЬКУЛЯТОРА

Слайд 11

37 х 47 = 1739

:2

37 47 х2
:2 18 94 х2
:2 9 188 х2
:2 4 376 х2
:2 2 752 х2
:2 1 1504

47+188+1504=1739-ответ

Крестьянский способ умножения.

Слайд 12 «Метод решётки»

Пусть нужно умножить 25 и 63.

2

5

1 6

5 3

7 5

Ответ: 1575

Слайд 13 Пример: 34×5=170
Как умножали
египтяне.

Т.к. 5 = 4

+ 1, то для получения ответа оставалось сложить числа,

стоящие в правом столбике против цифр 4 и 1 , т.е. 136 + 34 = 170.

Египтяне заменили умножение на любое число - удвоением.

Слайд 14 Умножение на 9
Пальцевой счет

Слайд 15 Общие приемы быстрого счета
разложение каждого слагаемого на разряды;
использование

Общие приемы быстрого счетаразложение каждого слагаемого на разряды;использование переместительного и

переместительного и сочетательного свойства сложения (умножения);
использование свойств вычитания;
использование распределительного

свойства при умножении и делении;
использование признаков делимости;
использование правил действий с дробями;
использование формул сокращенного умножения.

Слайд 16 Умножение на 1,5
Чтобы
умножить число на 1,5,
нужно

Умножение на 1,5Чтобы умножить число на 1,5, нужно к исходному числу

к исходному числу прибавить его половину.

24 · 1,5 =

24 + 12 = 36
86 · 1,5 = 86+ 43= 129

Слайд 17 Умножение на 11
Чтобы умножить двузначное
число

Умножение на 11 Чтобы умножить двузначноечисло на 11, надо цифры

на 11, надо цифры этого
числа «раздвинуть» и поставить
между ними

сумму этих цифр:

34 ∙ 11 = 3(3+4)4 = 374

51 ∙ 11 = 5(5+1)1 = 561

72 ∙ 11 = 7(7+2)2 = 792

94 ∙ 11= 9(9+4)4= 9(13)4 = (9+1)34=1034

Слайд 18 Умножение и деление на 5
Чтобы число
умножить на

5,
нужно умножить его на 10
и разделить на 2.

138

· 5 = (138 · 10) : 2 =
1380 : 2 = 690

Чтобы число
разделить на 5,
нужно умножить его на 2
и разделить на 10

71 : 5 = 71 · 2 : 10 =
142 : 10 = 14,2

Слайд 19 Умножение на 25, на125
Чтобы число умножить на 25,

Умножение на 25, на125Чтобы число умножить на 25, нужно разделить его

нужно разделить его на 4 и приписать два нуля.

248 · 25 = 248 : 4 · 100 = 6200
36 · 25 = 36 : 4 · 100 = 900

При умножении числа на 125 необходимо разделить его на 8 и приписать три нуля

72 · 125 = 72 : 8· 1000 = 9000
248 · 125 = 248 : 8· 1000 = 31000

Слайд 20 Возведение в квадрат числа, оканчивающегося цифрой 5
Чтобы

Возведение в квадрат числа, оканчивающегося цифрой 5Чтобы возвести в квадрат

возвести в квадрат число,
оканчивающееся цифрой 5
умножают число, образованное
цифрами,

стоящими до 5 на
следующее за ним при счете и
дописывают 25.

952 = 9025
9·10

1252 = 15625
12·13

Слайд 21 Возведение в квадрат числа, близкого к 50
Хочешь возвести

Возведение в квадрат числа, близкого к 50Хочешь возвести в квадрат число,

в квадрат число, близкое к 50, поступай так:
Вычти из

числа 25
Допиши к разнице двузначным число квадрат избытка от 50 (недостатка до 50).
Примеры:
582 = 3364.
58 – 25 = 33, 82 = 64,
582 = 3364.

482 = 2304.
48 – 25 = 23, 22 = 4,
482 = 2304.

Слайд 22 Умножение на 101, на 1001…
Чтобы умножить число на

101, нужно приписать к нему два нуля и прибавить

исходное число.

145 · 101 = 14500 + 145 = 14645
27 · 101 = 2700 + 27 = 2727

Чтобы умножить число на 1001, нужно приписать к нему три нуля и прибавить исходное число.

53 · 1001 = 53000 + 53 = 53053
461 · 1001=461000 +461=461461

Слайд 23 Умножение на 9, 99, 999,…
Чтобы умножить число на

Умножение на 9, 99, 999,…Чтобы умножить число на 9, к нему

9, к нему приписывают 0 и вычитают исходное число.

241 · 9 = 2410 – 241 = 2169

Чтобы умножить число на 99 надо приписать к нему два нуля и вычесть исходное число.
23 ∙ 99 = 2300 – 23 = 2277

Чтобы умножить число на 999 надо приписать к нему три нуля и вычесть исходное число.
18 ∙ 999 = 18000 – 18 = 17982

Слайд 24 Заключение
Действительно, существуют специальные способы выполнения действий, которые позволяют

ЗаключениеДействительно, существуют специальные способы выполнения действий, которые позволяют свести вычисления к

свести вычисления к устным, быстрым, не требующие уникальных способностей,

рассчитанные на ум «обычного» человека.

Главное – небольшая тренировка.
Решение примера, задействованного в исследовании, займет
10 -15 секунд:
34 · 1,5 + 124 · 25 =
34 + 17 + 124 : 4 · 100 =
51 + 3100 = 3151