на координатной плоскости
6. Синус и косинус.
7. Тангенс
и котангенс.8. Тригонометрические функции числового аргумента
9. Тригонометрические функции углового аргумента
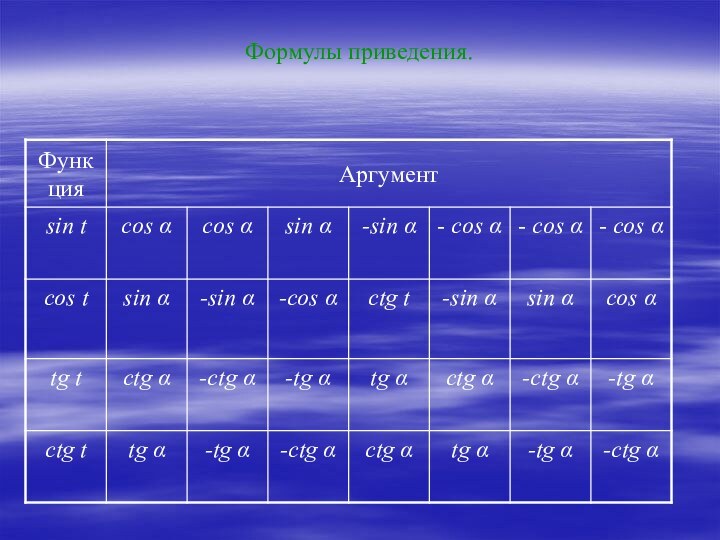
10. Формулы приведения.
11. Таблица значений тригонометрических функций некоторых углов.
12. Формулы преобразования тригонометрических функций.
13. Формулы преобразования произведения тригонометрических функций в сумму.
14. Формулы двойного угла. . Формулы понижения степени.
15. Формулы половинного аргумента.
16. Универсальная подстановка