- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Бенефис одной задачи
Содержание
- 2. Бенефис одной задачи. (В одной задаче – почти вся планиметрия!)
- 4. Способ №11. Продолжим BC вправо. Проведем DK
- 5. Способ №2 (похож на 1)Проведем СЕ ||
- 6. Способ №3 MN – средняя линия
- 7. Способ №41.Продолжим CA на расстояние AM =
- 9. Способ №6 Продолжим AC за точку A
- 12. Способ №9 Тригонометрический1. Из подобия ΔBOC и
- 13. Скачать презентацию
- 14. Похожие презентации
Бенефис одной задачи. (В одной задаче – почти вся планиметрия!)












Слайд 3
Задача. В
трапеции диагонали длиной 6 см и 8 см взаимно перпендикулярны. Найдите длину средней линии трапеции.
Слайд 4
Способ №1
1. Продолжим BC вправо. Проведем DK ||
AC. Так как ACKD – параллелограмм, то DK=6 см.
2.
BD┴DK, так как BD ┴ AC. Δ BDK – прямоугольный.BK= ;
BK= =10(см).
3. BK=BC+AD. Средняя линия равна половине BK, то есть 5 см.
Ответ: 5 см.
В
С
А
D
K
О
Слайд 5
Способ №2 (похож на 1)
Проведем СЕ || BD
до пересечения с продолжением AD. DE = BC, так
как DBCE – параллелограмм. AE вычислим по теореме Пифагора из ΔACE (CE || BD, но BD ┴ AC, следовательно,CE ┴AC):AE = ; AE = = 10(см).
AE = a+b. Но средняя линия равна (a+b)/2 ,
т.е. равна 5 см.
Ответ: 5 см.
A
B
C
D
E
a
b
6
8
Слайд 6
Способ №3
MN – средняя линия трапеции.
Проведем MK || BD и соединим точки N
и K.NK – средняя линия ΔACD, следовательно NK=0,5 AC; NK = 3(см).
MK – средняя линия ΔABD, следовательно MK=0,5 BD; MK=4(см).
Угол MKN равен углу AOD как углы с соответственно параллельными сторонами.
ΔMKN – прямоугольный.
MN = = =5(см).
Ответ: 5 см.
A
B
C
D
O
M
N
K
Слайд 7
Способ №4
1.Продолжим CA на расстояние AM = CО.
Через точку М проведем MN || AD. BD ∩ MN = N.
2. ΔOMN – прямоугольный, OM = 6 см, ON = 8 см. Следовательно, MN = 10 cм (теорема Пифагора).
3. Проведем MK || ND. Продолжим AD до пересечения с MK. ΔMAK = ΔBOC (по I признаку), следовательно AK = = BC.
4. MKDN – параллелограмм, DK= MN = 10 см. Но
DK = AD+BC. Значит, средняя линия равна 5 см.
Ответ: 5 см.
A
B
C
D
M
K
O
N
Слайд 8
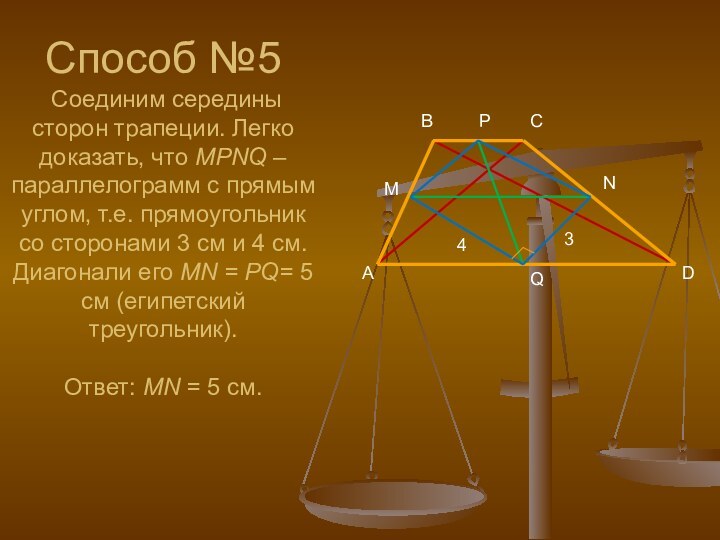
Способ №5 Соединим середины сторон трапеции. Легко
доказать, что MPNQ – параллелограмм с прямым углом, т.е. прямоугольник со сторонами 3 см и 4 см. Диагонали его MN = PQ= 5 см (египетский треугольник). Ответ: MN = 5 cм.P
M
Q
N
3
4
Слайд 9 Способ №6 Продолжим AC за точку A так, что
АМ = ОС. Продолжим BD за точку D так,
что DN = BO. Итак, ΔOMN – прямоугольный с катетами 6 см и 8 см. По теореме Пифагора MN = 10 см. Проведем AE ┴ MN, DF ┴ MN, OK ┴ BC. ΔAME = ΔKOC и ΔDFN = ΔBKO по стороне и двум прилежащим к ней углам. Следовательно, ME = KC и FH = BK, т.е. MN = AD + BC = 10 (см). Средняя линия равна (AD+BC)/2= =MN/2=10/2 = 5. Ответ: 5 см.O
M
E
F
N
Слайд 10 Способ №7 Пусть OC = x, BO =
y; тогда АО = 6 – х, DO =
8 – y. MN – средняя линия. 1.Из подобия ΔBOC и ΔAOD имеем: х/(6-х) = у/(8-у), 8х – ху = 6у – ху, 8х = 6у, у = 4/3х. 2. Из прямоугольного треугольника ΔBOC имеем: ВС = √ x²+ (4/3x)² = √ x² + 16/9x² = √ 25/9x² = 5/3x. 3.Из подобия ΔBOC и ΔAOD имеем: BC/AD = OC/AO, (5/3x)/AD = x/(6-x), AD = 5/3(6-x) = 10-5/3x. 4. MN = (AD + BC) = (5/3x+10-5/3x)/2 = 5 (см). Ответ: 5 см.Слайд 11 Способ №8 1.Из подобия ΔBOC и ΔAOD: x/(6-x) =
y/(8-y), y=4/3x. 2.Продолжим диагонали на отрезки, равные CO и BO. 3.Из
ΔMON: MN = 10 см. 4. AOD подобен ΔMON; MN = 4/3 AD, AD = 3/4MN = =3/4*10 = = 7,5 (см). 5.В ΔBOC: BC = x²+(4/3x)² = 5/√3x. 6.ΔBOC подобен ΔAOD. BC/AD = OC/AO, (5/3x²)/7,5 = x/(6-x); 10x-5/3x² = 7,5x; 2,5x = 5/3x²; 7,5 = 5x; x = 1,5 (cм). 7. BC = 5/3x = 5/3*1,5 = 2,5 (см). 8. Средняя линия равна (AD+BC)/2 = (7,5+2,5)/2 = 5. Ответ: 5 см.M
N
y
x
6-x
8-y
O
Слайд 12
Способ №9 Тригонометрический
1. Из подобия ΔBOC и ΔAOD:
X/(6-x)
= y/(8-y) , y =4/3 х.
2. Δ BOC –
прямоугольный.tg α =y/x =4/3x : x = у =4/3 .
3. Найдем cos α либо по формуле:
1+tg²α = 1/cos a,
либо методом треугольника: cos α = 3/5.
4. Из ΔBOC:
OC/BC = cos α, BC = OC/cos α =4*5/3 = 5/3 x.
5. Из ΔAOD:
AO/OD = cos α, AD = AO/ cos α = (6-x)/3/5 = 5(6-x)/3 .
6. Средняя линия равна
(AD+BC)/2 = 5 (см).