- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Биссектриса: знакомая и не очень
Содержание
- 2. Определение биссектрисы углаАААDCBМОУ Тулиновская средняя общеобразовательная школа
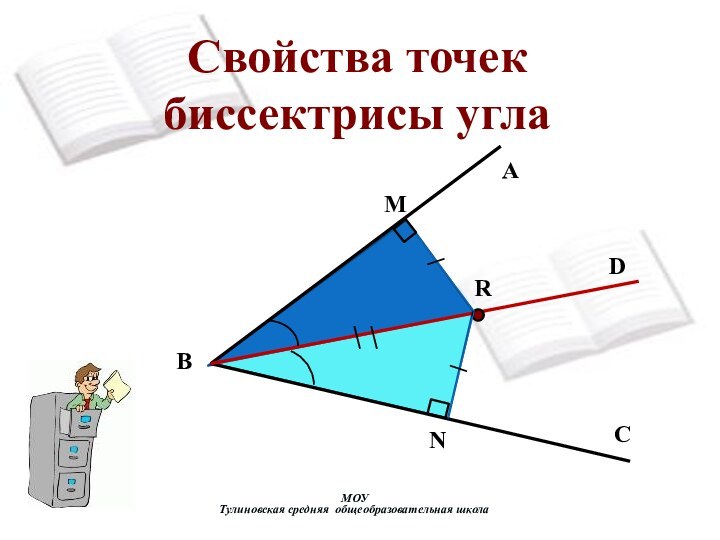
- 3. Свойства точек биссектрисы углаМОУ Тулиновская средняя общеобразовательная школаАNRMDCB
- 4. Цель исследования:МОУ Тулиновская средняя общеобразовательная школаБиссектриса углаОпределить свойство точек, равнооудаленных от сторон угла
- 5. Ход исследования1. Изучив теоретический материал учебника и
- 6. Гипотеза Существуют точки, не принадлежащие биссектрисе угла, а всё-таки равноудалённые от сторон углаМОУ Тулиновская средняя общеобразовательная школа
- 7. Результаты исследованияМОУ Тулиновская средняя общеобразовательная школаАXСBDВсе точки
- 8. МОУ Тулиновская средняя общеобразовательная школаРезультаты исследованияAXFKBCDТочки биссектрисы
- 9. МОУ Тулиновская средняя общеобразовательная школаРезультаты исследованияГеометрическое место
- 10. Результаты исследованияМОУ Тулиновская средняя общеобразовательная школаСВEADFК Получили фигуру,
- 11. Результаты исследованияМОУ Тулиновская средняя общеобразовательная школаBADFRCKLORMЦентр вписанной
- 12. Результаты исследованияМОУ Тулиновская средняя общеобразовательная школаRRFKLMHODCBAЦентр вписанной
- 13. Результаты исследованияМОУ Тулиновская средняя общеобразовательная школаRRFKLMHODCBAЦентр вписанной
- 14. Результаты исследованияМОУ Тулиновская средняя общеобразовательная школаFKEDMOCBAТочка пересечения
- 15. ВыводМОУ Тулиновская средняя общеобразовательная школаСуществуют точки, не
- 16. Скачать презентацию
- 17. Похожие презентации
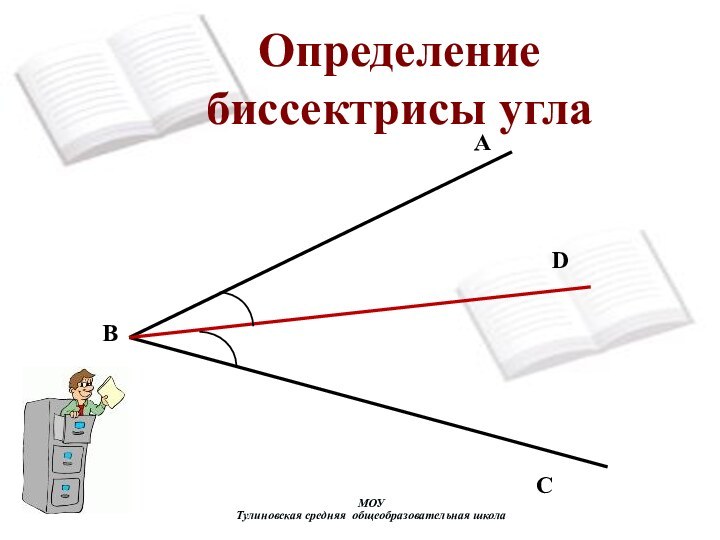
Определение биссектрисы углаАААDCBМОУ Тулиновская средняя общеобразовательная школа






Слайд 4
Цель исследования:
МОУ
Тулиновская средняя общеобразовательная школа
Биссектриса угла
Определить свойство
точек, равнооудаленных от сторон угла
Слайд 5
Ход исследования
1. Изучив теоретический материал учебника и дополнительных
источников информации, дать определение биссектрисы угла, биссектрисы треугольника.
2. Выяснить,
каким свойством обладает точка пересечения биссектрис углов треугольника.3. Рассмотреть и решить задачи по данной теме.
4. Оформить результаты, сделать соответствующие выводы.
МОУ
Тулиновская средняя общеобразовательная школа
Слайд 6
Гипотеза
Существуют точки,
не принадлежащие биссектрисе угла, а всё-таки
равноудалённые от сторон угла
МОУ
Тулиновская средняя общеобразовательная школа
Слайд 7
Результаты исследования
МОУ
Тулиновская средняя общеобразовательная школа
А
X
С
B
D
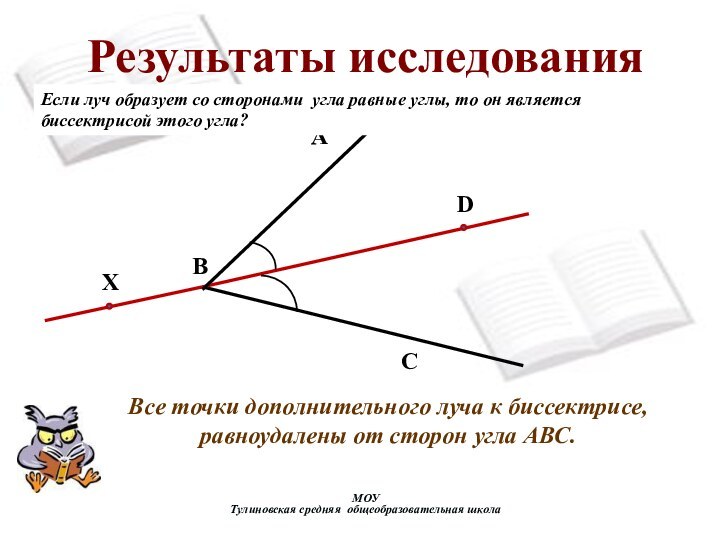
Все точки дополнительного
луча к биссектрисе, равноудалены от сторон угла АВС.
Если луч
образует со сторонами угла равные углы, то он является биссектрисой этого угла?
Слайд 8
МОУ
Тулиновская средняя общеобразовательная школа
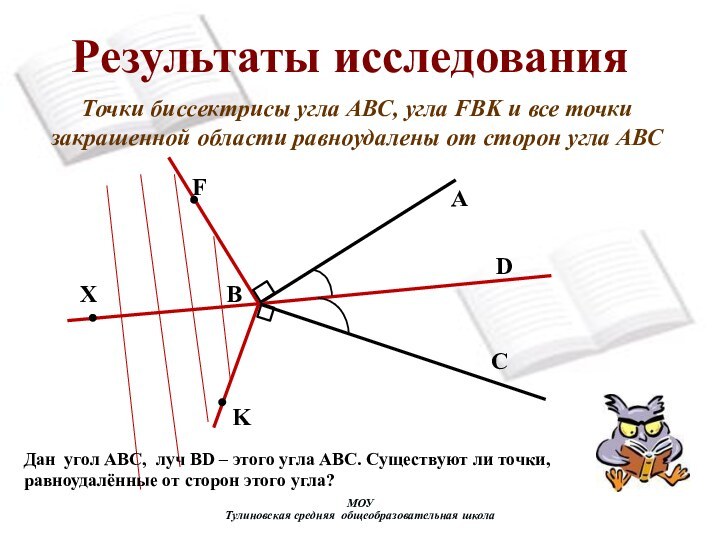
Результаты исследования
A
X
F
K
B
C
D
Точки биссектрисы угла
АВС, угла FBK и все точки закрашенной области равноудалены
от сторон угла АВСДан угол АВС, луч BD – этого угла ABC. Существуют ли точки, равноудалённые от сторон этого угла?
Слайд 9
МОУ
Тулиновская средняя общеобразовательная школа
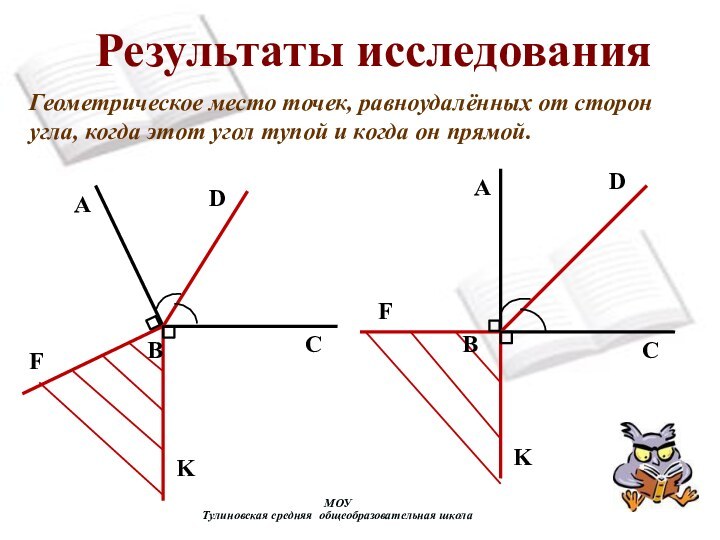
Результаты исследования
Геометрическое место точек,
равноудалённых от сторон угла, когда этот угол тупой и
когда он прямой.F
K
F
K
D
D
C
C
B
B
A
A
Слайд 10
Результаты исследования
МОУ
Тулиновская средняя общеобразовательная школа
С
В
E
A
D
F
К
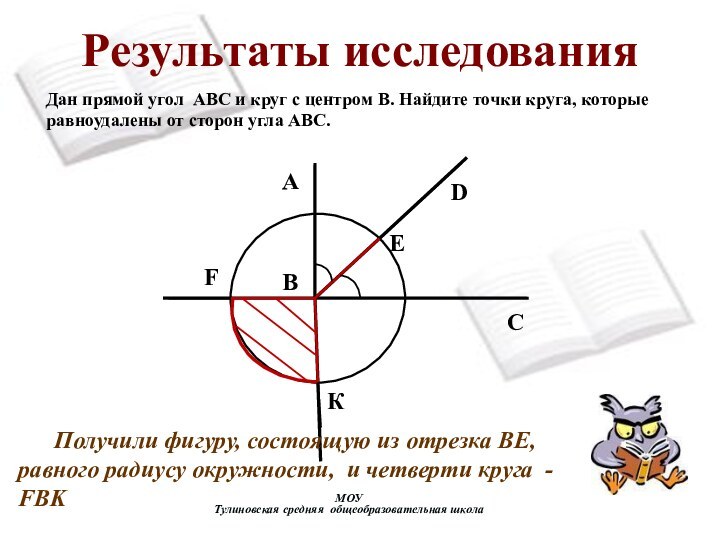
Получили фигуру, состоящую
из отрезка ВЕ, равного радиусу окружности, и четверти круга
- FBKДан прямой угол АВС и круг с центром В. Найдите точки круга, которые равноудалены от сторон угла АВС.
Слайд 11
Результаты исследования
МОУ
Тулиновская средняя общеобразовательная школа
B
A
D
F
R
C
K
L
O
R
M
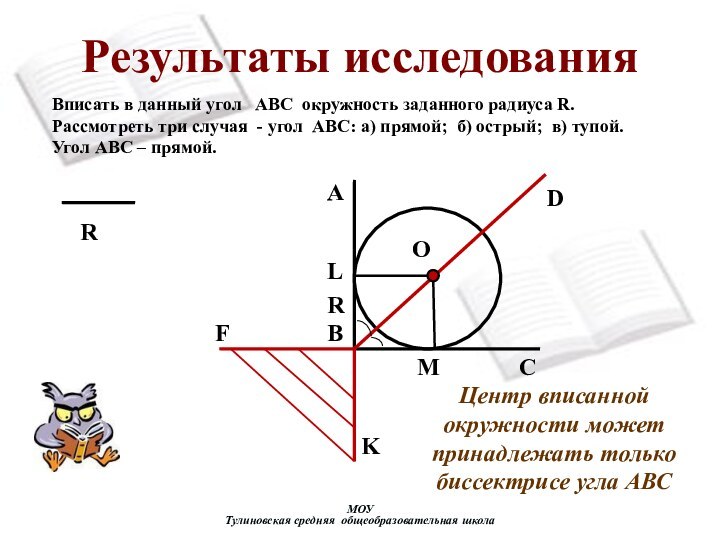
Центр вписанной окружности
может принадлежать только биссектрисе угла АВС
Вписать в данный угол
АВС окружность заданного радиуса R. Рассмотреть три случая - угол АВС: а) прямой; б) острый; в) тупой.Угол АВС – прямой.
Слайд 12
Результаты исследования
МОУ
Тулиновская средняя общеобразовательная школа
R
R
F
K
L
M
H
O
D
C
B
A
Центр вписанной окружности
может принадлежать только биссектрисе угла АВС
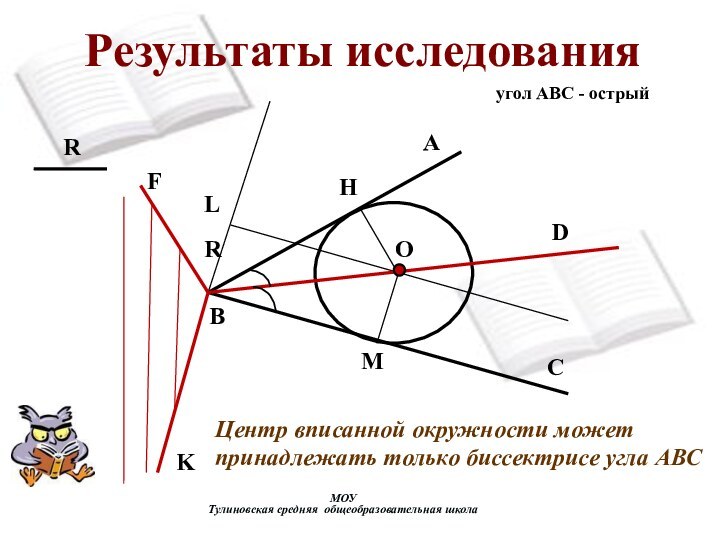
угол АВС - острый
Слайд 13
Результаты исследования
МОУ
Тулиновская средняя общеобразовательная школа
R
R
F
K
L
M
H
O
D
C
B
A
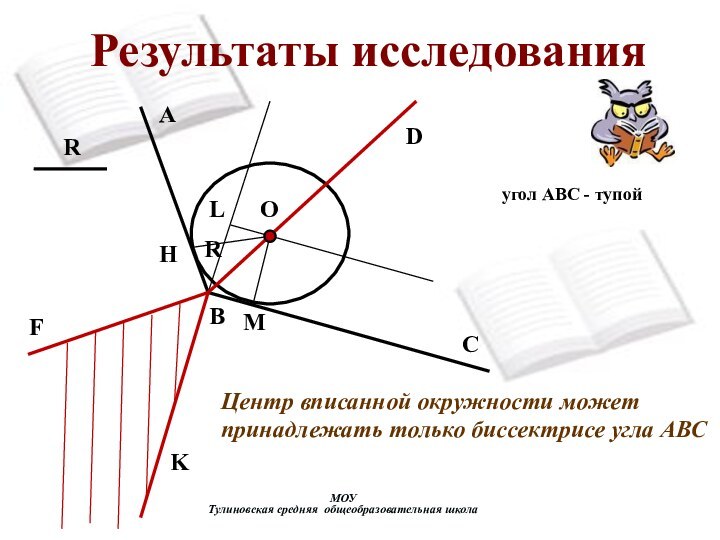
Центр вписанной окружности
может принадлежать только биссектрисе угла АВС
угол АВС - тупой
Слайд 14
Результаты исследования
МОУ
Тулиновская средняя общеобразовательная школа
F
K
E
D
M
O
C
B
A
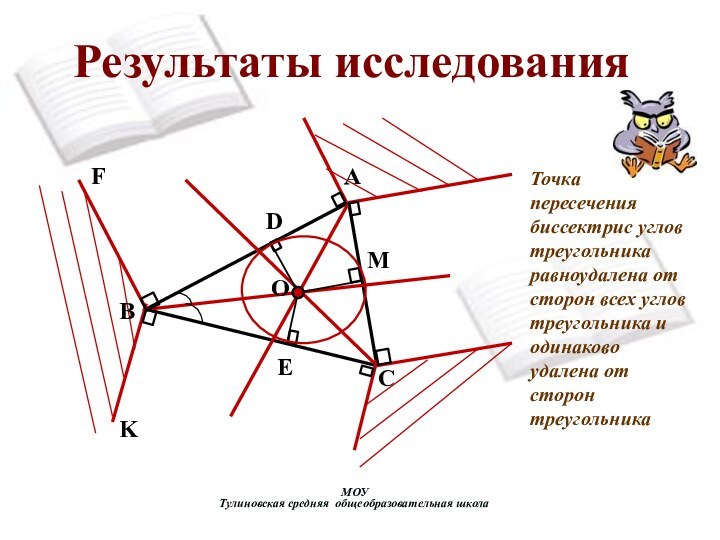
Точка пересечения биссектрис
углов треугольника равноудалена от сторон всех углов треугольника и
одинаково удалена от сторон треугольника
Слайд 15
Вывод
МОУ
Тулиновская средняя общеобразовательная школа
Существуют точки, не принадлежащие
биссектрисе угла, но всё-таки равноудалённые от сторон данного угла.
Центр
окружности, вписанной в угол, принадлежит только биссектрисе данного угла. Точка пересечения биссектрис углов треугольника является единственной точкой равноудаленной от сторон всех углов треугольника и от сторон треугольника.