из четырёх точек и четырёх отрезков, соединяющих их последовательно;
1.
На одной прямой должно лежать не больше двух точек.2. Отрезки, соединяющие точки, не должны пересекаться.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Четырехугольники 8 класс
Содержание
- 2. Четырехугольник, его елементы Четырехугольник — фигура,
- 3. Точки чотырехугольника называются вершинами, а отрезки, соединяющие
- 4. Соседние стороны— стороны четырехугольника, которые выходят из
- 5. Четырехугольник называется указанием его вершин, при
- 6. Если
- 7. Параллелограмм и его свойства.Признаки параллелограмма. Четырехугольник,
- 8. У параллелограмма из каждой
- 9. Свойства параллелограмма У параллелограмма противоположные стороны равны.У
- 10. Диагонали параллелограмма пересекаются и точкой пересечения делятся
- 11. Признаки параллелограмма Если диагонали
- 12. Если в четырехугольнике противолежащие
- 13. Свойство диагоналей параллелограмма:Диагонали параллелограмма пересекаются и
- 14. Это интересно.Если провести биссектрисы двух противолежащих углов
- 15. Прямоугольник, его свойстваПредставитель класса параллелограммов - прямоугольник.Параллелограмм, у которого все углы прямые, называются прямоугольником.
- 16. Свойства прямоугольникаПротиволежащие стороны прямоугольника равны.Все углы прямоугольника
- 17. Диагонали прямоугольника пересекаются и точкою пересечения делятся
- 18. Признаки прямоугольникаЕсли в параллелограмме все углы равны,
- 19. Это интересно. Если в прямоугольнике с
- 20. Ромб, его свойства.Параллелограмм, у которого все стороны равны, называется ромбом.
- 21. Свойства ромбаПротиволежащие углы ромба равны.У ромба сумма
- 22. Признаки ромба Если в параллелограмме диагонали пересекаются
- 23. Это интересно.Если соединить отрезками средины сторон прямоугольника,
- 24. Квадрат, его свойстваСвойства квадратаПрямоугольник, у которого все
- 25. Признаки квадрата Если в прямоугольнике диагонали пересекаются
- 26. Трапеция, её свойстваЧетырехугольник, у которого только две
- 27. Равнобедренная трапеция — это трапеция, у которой
- 28. Свойства трапецииВ равнобедренной трапеции углы при каждой
- 29. Признаки равнобедренной трапецииЕсли в трапеции углы при
- 30. Это интересно.Если средины сторон равнобедренной трапеции соединить отрезками, то получим ромб.
- 31. Скачать презентацию
- 32. Похожие презентации
Четырехугольник, его елементы Четырехугольник — фигура, состоящая из четырёх точек и четырёх отрезков, соединяющих их последовательно;1. На одной прямой должно лежать не больше двух точек.2. Отрезки, соединяющие точки, не должны пересекаться.
Слайд 2
Четырехугольник, его елементы
Четырехугольник — фигура, состоящая
из четырёх точек и четырёх отрезков, соединяющих их последовательно;
На одной прямой должно лежать не больше двух точек.2. Отрезки, соединяющие точки, не должны пересекаться.
Слайд 3
Точки чотырехугольника называются вершинами,
а отрезки, соединяющие их
, — сторонами.
Соседние вершины — вершины четырехугольника, которые являются концами
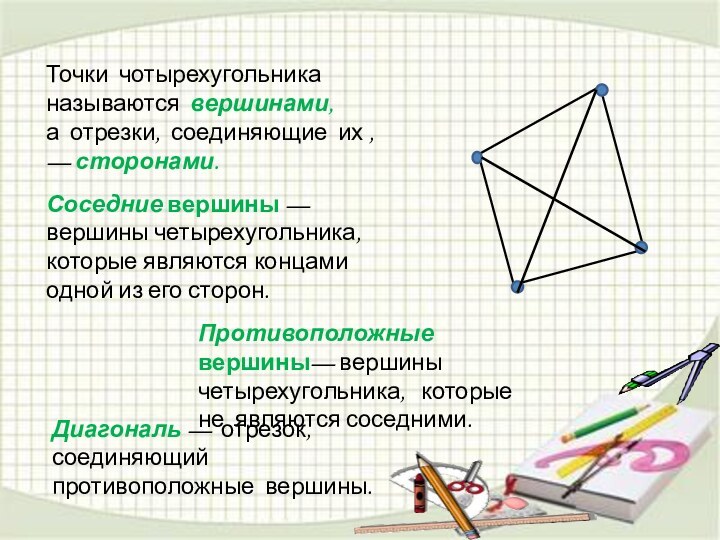
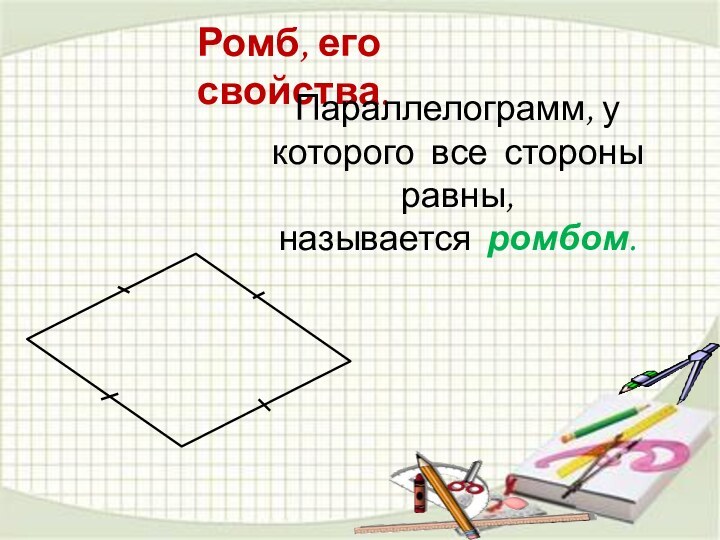
одной из его сторон.Противоположные вершины— вершины четырехугольника, которые не являются соседними.
Диагональ — отрезок, соединяющий противоположные вершины.
Слайд 4 Соседние стороны— стороны четырехугольника, которые выходят из одной
вершины.
Противолежащие стороны — стороны четырехугольника, которые не имеют общего
конца.Периметр — сумма всех сторон четырехугольника.
Слайд 5 Четырехугольник называется указанием его вершин, при этом
вершины называют последовательно.
У каждого четырехугольника
4 вершины,
4 стороны,
2 диагонали.
А
В
С
Д
Четырехугольник АВСД
Слайд 6 Если в
четырехугольнике провести одну диагональ, то четырехугольник разбивается на
два треугольника.Сумма углов заданного четырехугольника будет равняться сумме углов обоих полученных треугольников.
Учитывая, что сумма углов любого треугольника равна 1800, то сумма углов заданного четырехугольника равна 360°.
Запомните!
Сумма углов любого четырехугольника равна 3600.
1800
1800
Сумма углов четырехугольника
Слайд 7
Параллелограмм и его свойства.
Признаки параллелограмма.
Четырехугольник, у
которого противолежащие стороны параллельны, называется параллелограммом.
Высотою параллелограмма называется отрезок,
перпендикулярный к прямой, содержащую противоположную сторону.АВ ││СД
А
В
С
Д
АД ││ВС
Слайд 8 У параллелограмма из каждой его
вершины можно провести по две высоты.
Высоты,
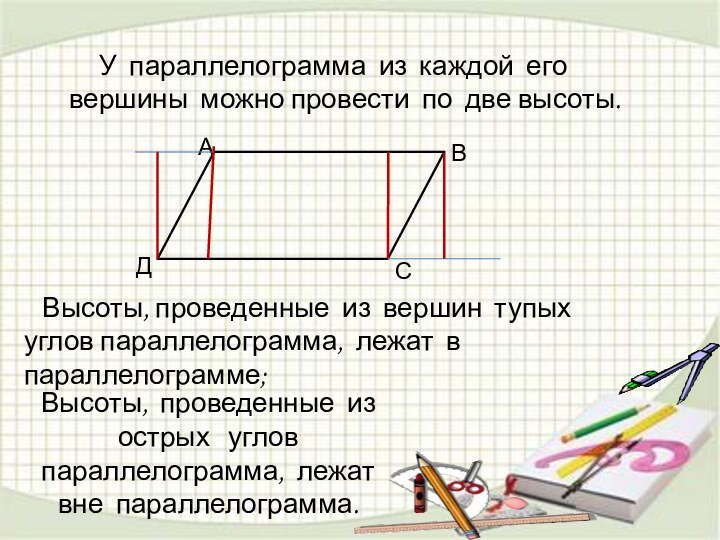
проведенные из вершин тупых углов параллелограмма, лежат в параллелограмме; Высоты, проведенные из острых углов параллелограмма, лежат вне параллелограмма.
Д
С
А
В
Слайд 9
Свойства параллелограмма
У параллелограмма противоположные стороны равны.
У параллелограмма
противоположные углы равны.
У параллелограмма сумма углов, прилежащих к одной
стороне, равна 180°. А В
Д С
АД=ВС
АВ=СД
< А = < С
< В= < Д
< А + < Д= 1800
< А + < В= 1800
< В + < С= 1800
< С + < Д= 1800
Слайд 10
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Диагонали
параллелограмма делят его на два равных треугольника.
А ВД С
О
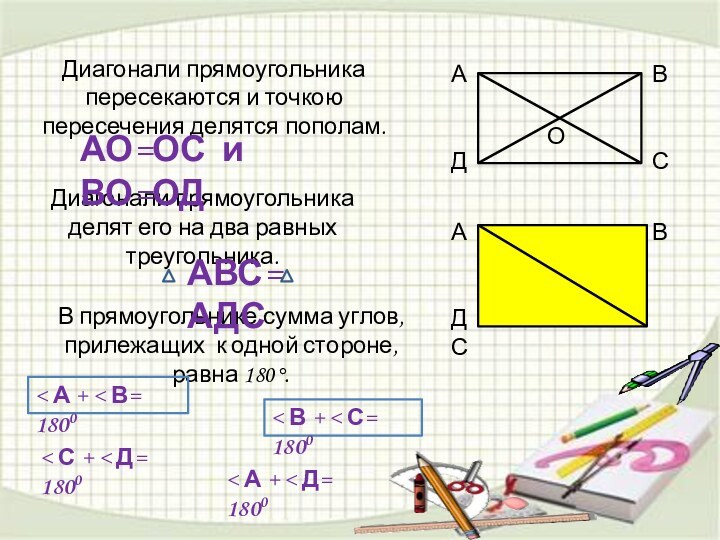
ВО=ОД
АО=ОС
А В
Д С
АВС= АДС
Слайд 11
Признаки параллелограмма
Если диагонали четырехугольника
пересекаются и точкой пересечения делятся пополам, то этот четырехугольник
параллелограмм.Если в четырехугольнике две противолежащие стороны параллельны и равны, то этот четырехугольник параллелограмм.
А В
Д С
О
Если АО=ОС и ВО=ОД , то АВСД - параллелограмм
Если АВ=ДС и АВ//ДС , то
АВСД - параллелограмм
Слайд 12 Если в четырехугольнике противолежащие стороны
попарно равны, то этот четырехугольник параллелограмм.
Если
в четырехугольнике противоположные углы попарно равны, то этот четырехугольник параллелограмм. А В
Д С
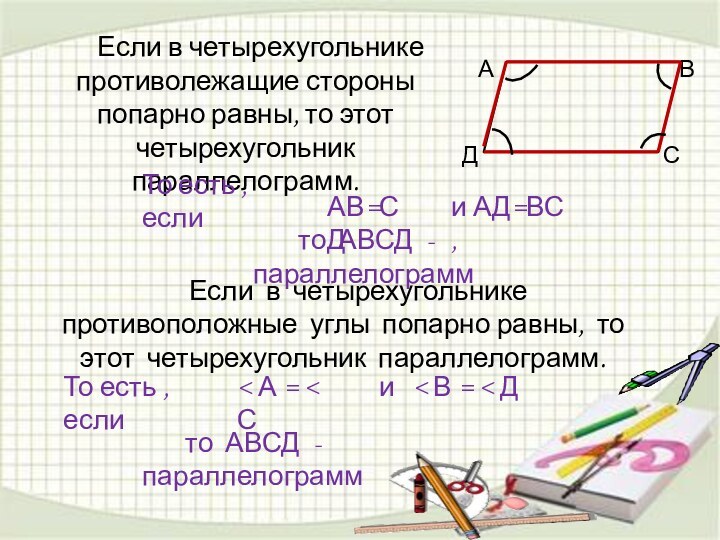
То есть , если
АВ=СД
и АД=ВС ,
то АВСД - параллелограмм
То есть , если
< А = < С
и < В = < Д
то АВСД - параллелограмм
Слайд 13
Свойство диагоналей параллелограмма:
Диагонали параллелограмма пересекаются и точкой
пересечения делятся пополам.
Свойство противоположных сторон и углов параллелограмма:
У параллелограмма
противоположные стороны и углы равны. А В
Д С
О
АО=ОС і ВО=ОД
АВ=СД
АД=ВС
< А = < С
< В = < Д
Слайд 14
Это интересно.
Если провести биссектрисы двух противолежащих углов параллелограмма,
то они будут параллельны или совпадут.
Если провести биссектрисы двух
углов, прилежащих к одной стороне параллелограмма, то они будут перпендикулярными. А В
Д С
К
Е
ВК//ДЕ
ВК СЕ
Слайд 15
Прямоугольник, его свойства
Представитель класса параллелограммов - прямоугольник.
Параллелограмм, у
которого все углы прямые, называются прямоугольником.
Слайд 16
Свойства прямоугольника
Противолежащие стороны прямоугольника равны.
Все углы прямоугольника равны.
Диагонали
прямоугольника равны.
А
ВД С
АВ=СД
АД=ВС
< А = <В = <С = < Д= 900
АС=ВД
Слайд 17
Диагонали прямоугольника пересекаются и точкою пересечения делятся пополам.
Диагонали
прямоугольника делят его на два равных треугольника.
В прямоугольнике сумма
углов, прилежащих к одной стороне, равна 180°.А В
Д С
О
АО=ОС и ВО=ОД
А В
Д С
АВС= АДС
< А + < В= 1800
< В + < С= 1800
< С + < Д= 1800
< А + < Д= 1800
Слайд 18
Признаки прямоугольника
Если в параллелограмме все углы равны, то
этот параллелограмм - прямоугольник.
Если в параллелограмме один угол прямой,
то этот параллелограмм - прямоугольник.Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.
А В
Д С
Если < А = <В = <С = < Д , то
АВСД - прямоугольник
Если < А = 900 , то АВСД - прямоугольник
Если АС=ВД, то
АВСД - прямоугольник
Если в четырехугольнике три угла прямые, то этот четырехугольник - прямоугольник.
Если < А = <В = <С = 900 , то
АВСД - прямоугольник
Слайд 19
Это интересно.
Если в прямоугольнике с неравными
смежными сторонами провести биссектрисы его углов, то при их
пересечении образуется прямоугольник.Обратите внимание!
Если в прямоугольнике проведена биссектриса, пересекающую одну из сторон, то она отсекает от прямоугольника равнобедренный треугольник.
Слайд 21
Свойства ромба
Противолежащие углы ромба равны.
У ромба сумма углов,
прилежащих к одной стороне, равна 1800
Диагонали ромба пересекаются под
прямым углом.Диагонали ромба являются биссектрисами его углов.
Диагонали ромба пересекаются и точкою пересечения делятся пополам.
А
В Д
С
< А = < С
< В = < Д
< А + < В = 1800
АС ВД
АО=ОС и ВО=ОД
О
Слайд 22
Признаки ромба
Если в параллелограмме диагонали пересекаются под
прямым углом, то этот параллелограмм - ромб.
Если в
параллелограмме диагонали являются биссектрисами его углов, то этот параллелограмм - ромб.Если в параллелограмме две смежные стороны равны, то этот параллелограмм - ромб.
Если в четырехугольнике все стороны равны, то этот четырехугольник - ромб.
Если в параллелограмме одна из диагоналей является биссектрисою его угла, то этот параллелограмм - ромб.
Если в четырехугольнике диагонали являются биссектрисами его углов и пересекаются под прямым углом, то этот четырехугольник - ромб.
Слайд 23
Это интересно.
Если соединить отрезками средины сторон прямоугольника, то
получим ромб.
Если соединить отрезками средины сторон ромба, то получим
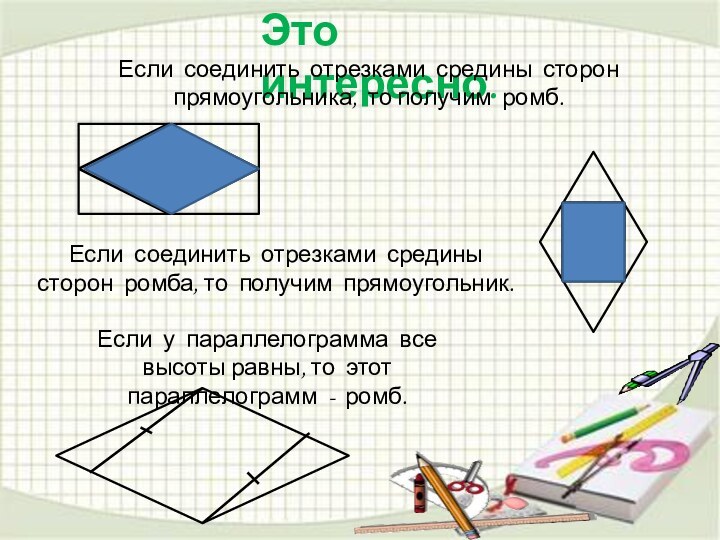
прямоугольник.Если у параллелограмма все высоты равны, то этот параллелограмм - ромб.
Слайд 24
Квадрат, его свойства
Свойства квадрата
Прямоугольник, у которого все стороны
равны, называются квадратом.
Диагонали квадрата пересекаются под прямым углом.
А
ВД С
Все углы квадрата — прямые.
Диагонали квадрата пересекаются и точкою пересечения делятся пополам.
Диагонали квадрата равны.
Диагонали квадрата являются биссектрисами его углов.
< А = <В = <С = < Д= 900
АО=ОС и ВО=ОД
О
АС=ВД
Слайд 25
Признаки квадрата
Если в прямоугольнике диагонали пересекаются под
прямым углом, то этот прямоугольник - квадрат.
Если у
ромба диагонали равны, то этот ромб - квадрат.Если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник - квадрат.
Слайд 26
Трапеция, её свойства
Четырехугольник, у которого только две противоположные
стороны параллельны, называется трапецией.
Основы трапеции —
две параллельные стороны;
Высотою трапеции называется отрезок, перпендикулярный к прямым, содержащим основы трапеции, и с концами на этих основах.боковые стороны — две другие.
Слайд 27 Равнобедренная трапеция — это трапеция, у которой боковые
стороны равны.
Боковая сторона трапеции, перпендикулярна к её основам, является
меньшею боковою стороною и равна высоте трапеции.Прямоугольная трапеция — это трапеция, одна боковая сторона которой перпендикулярна её основам.
В прямоугольной трапеции два угла прямые, один острый и один тупой.
А В
Д С
< А = < Д= 90 0
< В - тупой
< С - острый
АД = h
Слайд 28
Свойства трапеции
В равнобедренной трапеции углы при каждой основе
равны
Сумма углов трапеции, прилежащих к одной боковой
стороне, равна 180°. В равнобедренной трапеции диагонали равны и наклонены к основанию под одинаковыми углами.
А В
Д С
< А + < Д = 1800
< В + < С = 1800
А В
Д С
< А = < В
< С = < Д
АС=ВД
Слайд 29
Признаки равнобедренной трапеции
Если в трапеции углы при основании
равны, то трапеция равнобедренная.
Если в трапеции диагонали равны,
то трапеция равнобедренная.Если в трапеции диагонали образуют с основаниями равные углы, то трапеция равнобедренная.
Слайд 30
Это интересно.
Если средины сторон равнобедренной трапеции соединить отрезками,
![презентация к уроку математики Вычитание вида 6 – [ ], 7 – [ ] 1 класс презентация к уроку по математике (1 класс)](/img/tmb/9/861372/c55c86cb2886693b560e151ed987f01e-210x.jpg)
