Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Функция у=кх2, ее свойства и график

Содержание

2. Математику уже затем учить надо, что она
3. Девиз урока:«Дорогу осилит идущий, а математику- мыслящий»
4. у = 2х2 у = 0,5х2
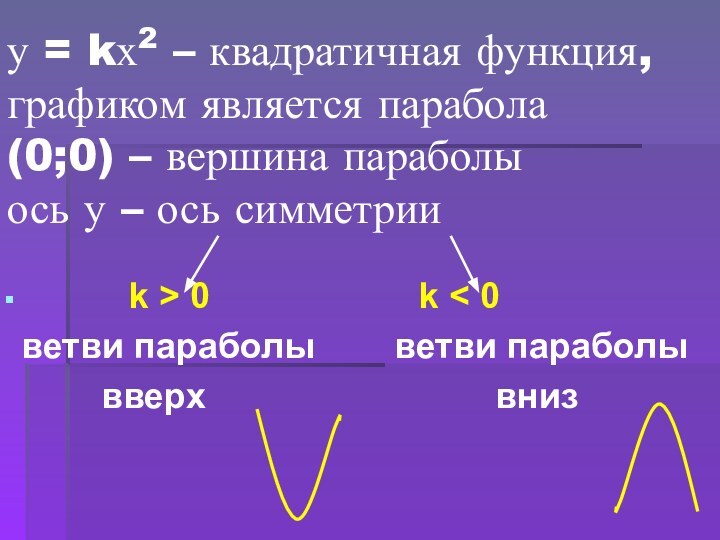
5. у = kх2 – квадратичная функция, графиком
6. График функции у = -f(x) симметричен графику функции у = f(x) относительно оси абсцисс.
7. Свойства функции у=кх2 при к > 0
8. 1.D(f) = (-∞;+∞) 2.
9. Свойства функции у = kх2 при k
10. Решите уравнение: -х2 = 2х - 3у
11. Вариант 1.При каком значении аргумента х значение
12. Вариант -2.1. При каком значении аргумента х
13. ОтветыВ-1 3,1,4В -2 4,2,2
14. Спасибо за урок
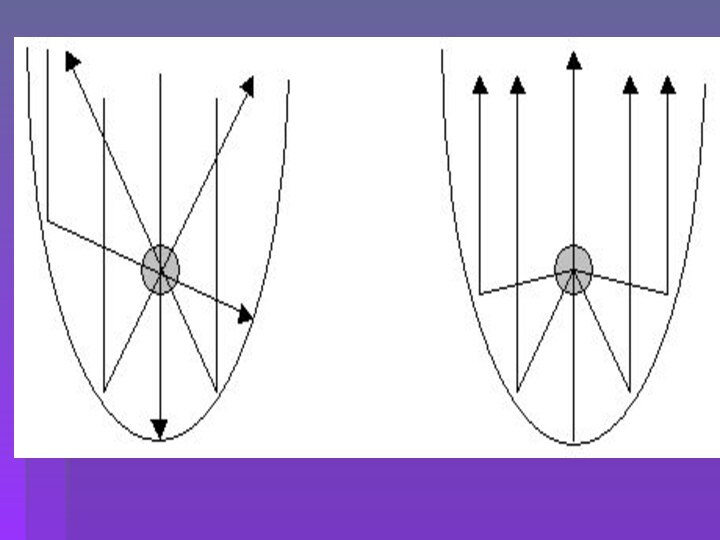
15. О замечательных свойствах параболы
19. Применение параболы в природе
29. Скачать презентацию
30. Похожие презентации

Математику уже затем учить надо, что она ум в порядок приводит. М.В.Ломоносов

Главная
Математика
Функция у=кх2, ее свойства и график

«Функция у=кх2 ,ее свойства и график» Алгебра 8 класс

Математику уже затем учить надо, что она ум в порядок приводит.

Девиз урока:«Дорогу осилит идущий, а математику- мыслящий»

у = kх2 – квадратичная функция, графиком является парабола (0;0) – вершина

График функции у = -f(x) симметричен графику функции у = f(x) относительно оси абсцисс.

Свойства функции у = kх2 при k < 01. D(f) = (-∞;

Решите уравнение: -х2 = 2х - 3у = -х2 –квадратичная функция, графиком

Вариант 1.При каком значении аргумента х значение функции у= 0,5х2 равно

Вариант -2.1. При каком значении аргумента х значение функции у= - 0,25

Слайды презентации

Слайд 2 Математику уже затем учить надо, что она ум

в порядок приводит.

М.В.Ломоносов

Слайд 3 Девиз урока:
«Дорогу осилит идущий, а математику- мыслящий»

Слайд 4 у = 2х2
у

= 0,5х2

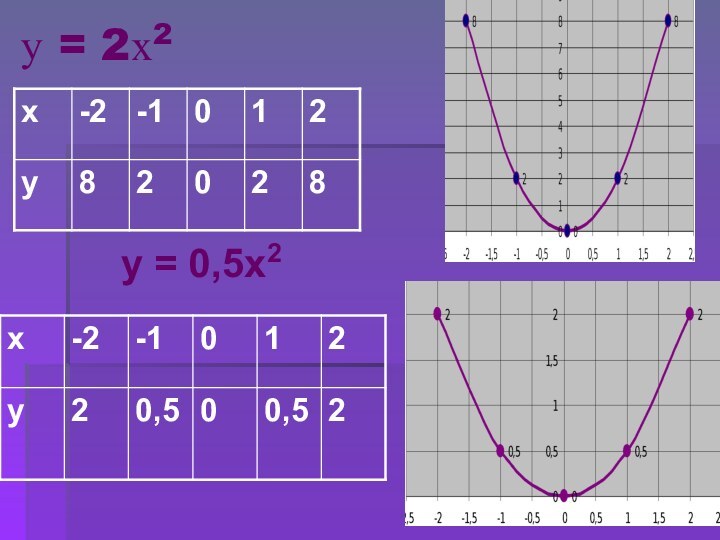
Слайд 5 у = kх2 – квадратичная функция, графиком является

у = kх2 – квадратичная функция, графиком является парабола (0;0) –

парабола (0;0) – вершина параболы ось у – ось симметрии

k > 0 k < 0
ветви параболы ветви параболы
вверх вниз

Слайд 6 График функции у = -f(x) симметричен графику функции

у = f(x) относительно оси абсцисс.

Слайд 7 Свойства функции у=кх2 при к > 0

Слайд 8 1.D(f) = (-∞;+∞) 2. у =

0 при х = 0 у > 0 при

х є (-∞; 0) U (0;+∞), 3.непрерывна 4.унаим = 0, унаиб = не сущ. 5. убывает при х є (-∞;0], возрастает при хє [0; +∞) 6.ограничена снизу, не ограничена сверху 7.Е(f) = [0; +∞) 8.выпукла вниз.

Слайд 9 Свойства функции у = kх2 при k < 0
1.

D(f) = (-∞; +∞)
2. у = 0 при х

= 0 , У < 0 при х є (-∞; 0) U (0; +∞),
3. Непрерывна
4. Унаим = не сущ., унаиб = 0 (при х=0)
5. возрастает при х є (-∞; 0],
убывает при х є [0; +∞)
6.Ограничена сверху, не ограничена снизу
7. Е(f) = (-∞; 0]
8. выпукла вверх.

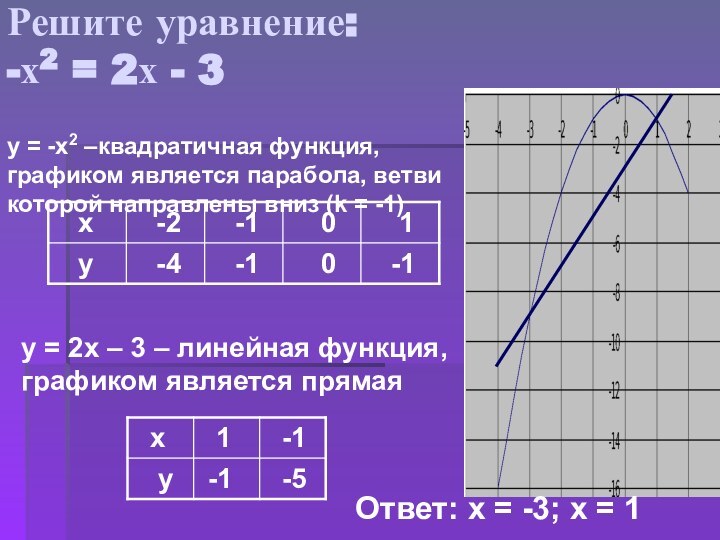
Слайд 10 Решите уравнение: -х2 = 2х - 3
у = -х2

Решите уравнение: -х2 = 2х - 3у = -х2 –квадратичная функция,

–квадратичная функция, графиком является парабола, ветви которой направлены вниз

(k = -1)

у = 2х – 3 – линейная функция, графиком является прямая

Ответ: х = -3; х = 1

Слайд 11 Вариант 1.
При каком значении аргумента х значение функции

у= 0,5х2 равно 2 ?
1)-1 и 1

2) 2 3) -2 и 2
4) -0,5 и 0,5
Графику функции у = -50 х2 принадлежит точка с координатами
1)(-4;-800) 2) (-4; 800) 3) (-4; 200) 4) (-4; -200)
Прямая у =5х-1 пересекает параболу у =2х2
1)в одной точке 2) в двух точках
3)в трех точках 4) не пересекает

Слайд 12 Вариант -2.
1. При каком значении аргумента х значение

Вариант -2.1. При каком значении аргумента х значение функции у= -

функции у= - 0,25 х2 равно -4 ?
1)-1

и 1 2) 4 3) - 0,25 и 0,25 4) -4 и 4
2. Графику функции у =80 х2 принадлежит точка с координатами
1)(-5;-200) 2) (-5; 2000) 3) (-5; -2000) 4) (-5; -200)
Прямая у =2х+7 пересекает параболу у =3х2
1)в одной точке 2) в двух точках
3)в трех точках 4) не пересекает