Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

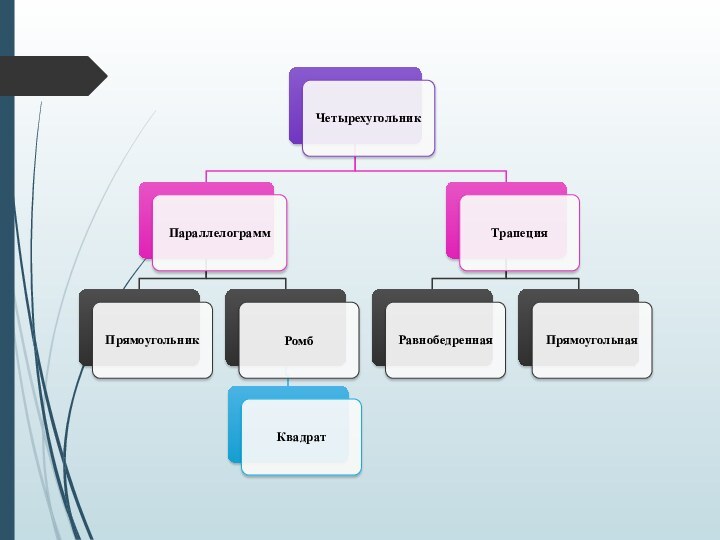
Презентация на тему четырехугольники2

Содержание

2. Цель – систематизировать свойства и признаки четырехугольников, изученные на уроках геометрии
3. Четырехугольником называется фигура, которая состоит
4. Смежными являются стороны: [AB] и [CB], [BC]
6. ПараллелограммЧетырехугольник, у которого противоположные стороны параллельны, называется параллелограммомСвойстваПризнаки
7. ПараллелограммЧетырехугольник, у которого противоположные стороны параллельны, называется параллелограммомСвойстваПризнаки
8. ПрямоугольникПараллелограмм, у которого все углы прямые, называется прямоугольникомСвойстваПризнаки
9. ПрямоугольникПараллелограмм, у которого все углы прямые, называется прямоугольникомСвойстваПризнаки
10. РомбПараллелограмм, у которого все стороны равны, называется ромбомСвойстваПризнаки
11. РомбПараллелограмм, у которого все стороны равны, называется ромбомСвойстваПризнаки
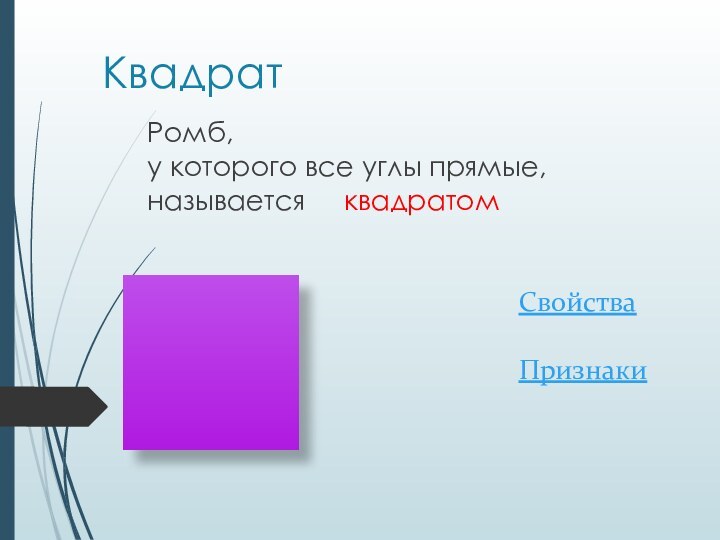
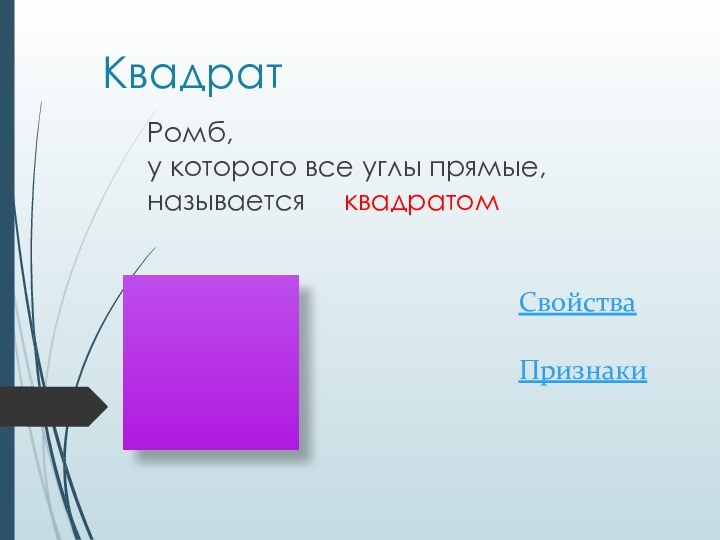
12. КвадратРомб, у которого все углы прямые, называется квадратомСвойстваПризнаки
13. КвадратРомб, у которого все углы прямые, называется квадратомСвойстваПризнаки
14. ТрапецияЧетырехугольник, у которого две противоположные стороны параллельны, а две другие – непараллельные, называется трапецией
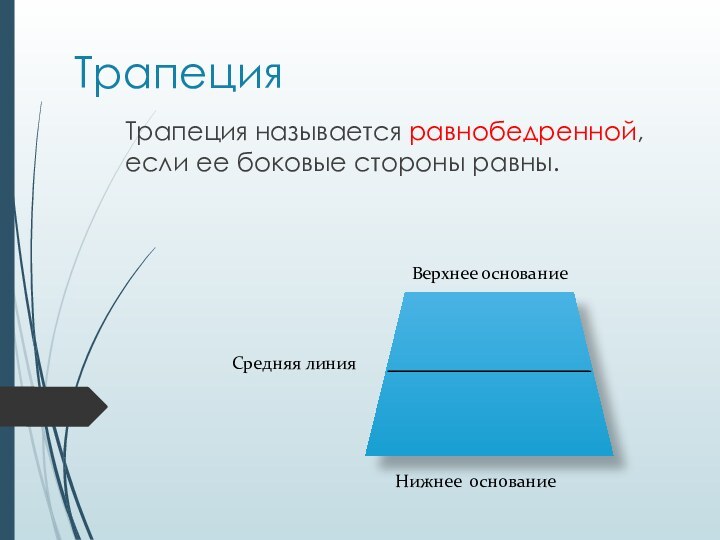
15. ТрапецияТрапеция называется равнобедренной, если ее боковые стороны равны.Верхнее основаниеНижнее основаниеСредняя линия
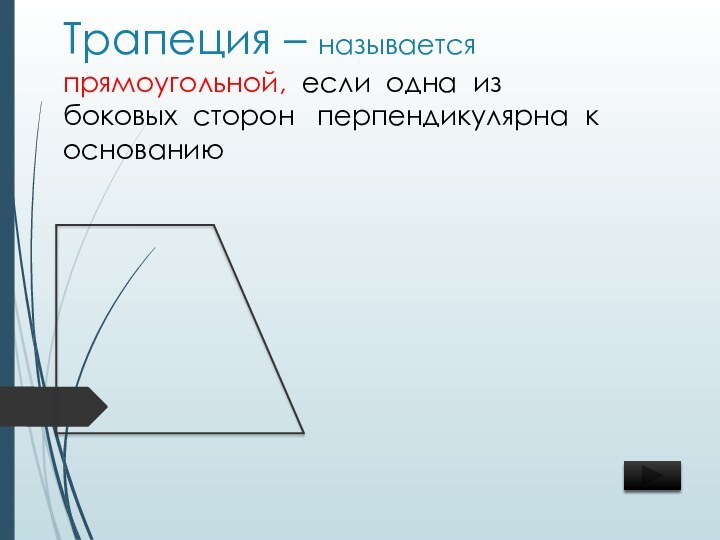
16. Трапеция – называется прямоугольной, если одна из боковых сторон перпендикулярна к основанию
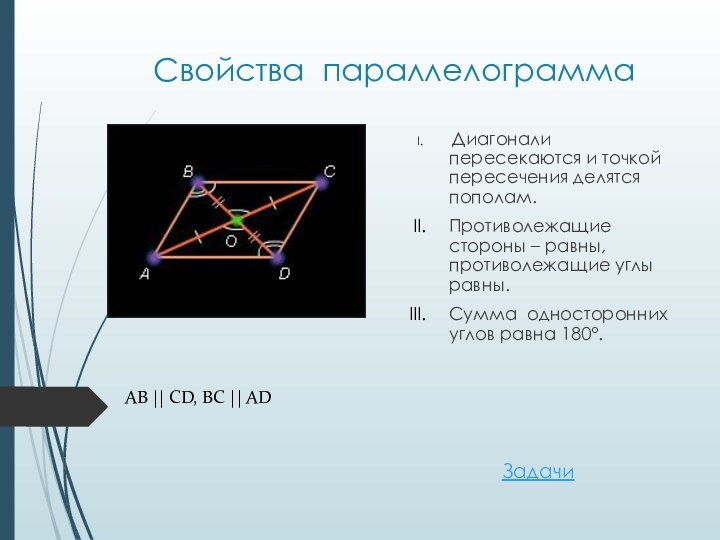
17. Свойства параллелограмма Диагонали пересекаются и точкой пересечения
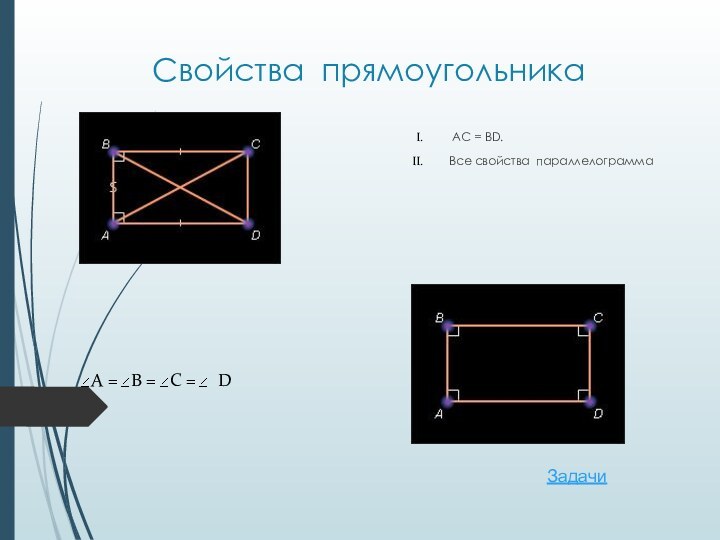
18. Свойства прямоугольника AC = BD.Все свойства параллелограммаЗадачи
19. Свойства ромба AC BD.AC –
20. Свойства квадрата AC BD. AC
21. Признаки параллелограммаAB || CD, BC || ADЗадачи
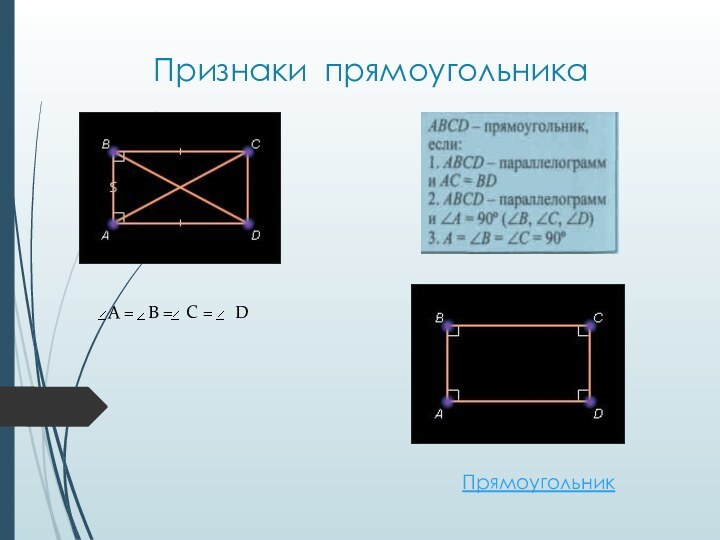
22. Признаки прямоугольникаПрямоугольник
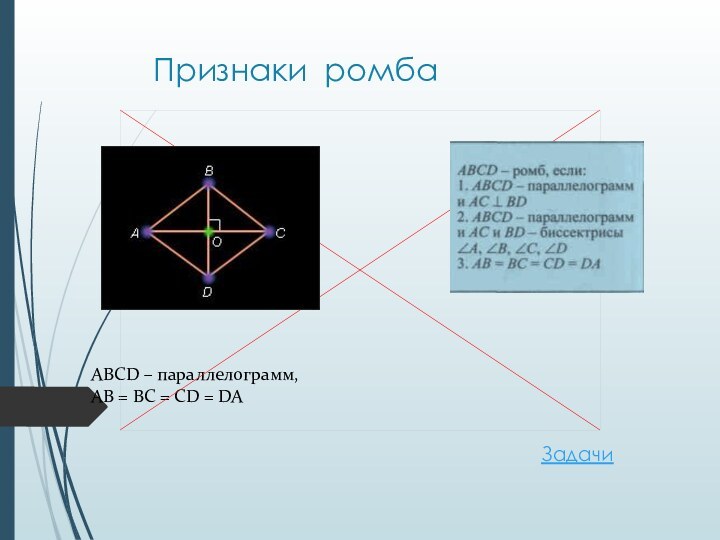
23. Признаки ромбаABCD – параллелограмм,AB = BC = CD = DAЗадачи
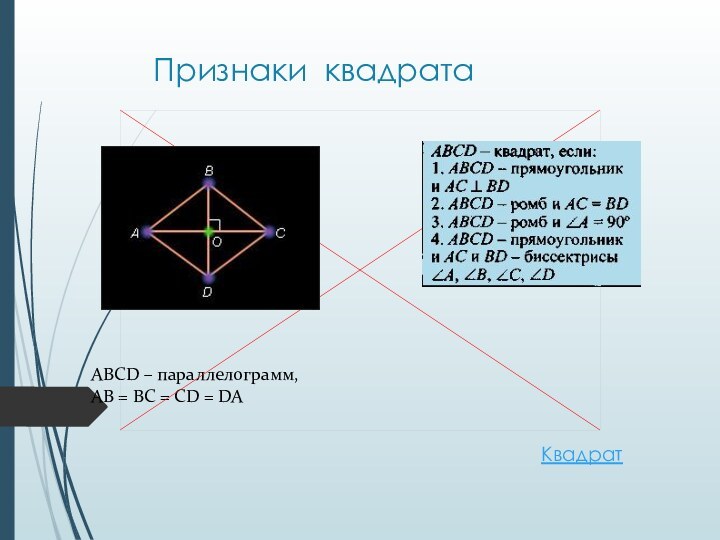
24. Признаки квадратаABCD – параллелограмм,AB = BC = CD = DAКвадрат
25. Свойства параллелограмма. Задачи 1) MNKP — параллелограмм,
26. Признаки параллелограмма. Задачи На рисунке ABCD — параллелограмм, BT = DK. Докажите, что АТСК—параллелограмм.Параллелограмм
27. Свойства прямоугольника. Задачи 1) В прямоугольнике ABCD
28. Свойства и признаки ромба. ЗадачиРомб1) В ромбе
29. Свойства и признаки квадрата. Задачи КвадратВнутри квадрата
30. Скачать презентацию
31. Похожие презентации

Цель – систематизировать свойства и признаки четырехугольников, изученные на уроках геометрии

Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 7»Автор: Данилов Н., Игнатьева К.,

Четырехугольником называется фигура, которая состоит из четырех точек, называемых

Смежными являются стороны: [AB] и [CB], [BC] и [CD], [CD] и [AD],

ПараллелограммЧетырехугольник, у которого противоположные стороны параллельны, называется параллелограммомСвойстваПризнаки

ПрямоугольникПараллелограмм, у которого все углы прямые, называется прямоугольникомСвойстваПризнаки

РомбПараллелограмм, у которого все стороны равны, называется ромбомСвойстваПризнаки

КвадратРомб, у которого все углы прямые, называется квадратомСвойстваПризнаки

ТрапецияЧетырехугольник, у которого две противоположные стороны параллельны, а две другие – непараллельные, называется трапецией

ТрапецияТрапеция называется равнобедренной, если ее боковые стороны равны.Верхнее основаниеНижнее основаниеСредняя линия

Трапеция – называется прямоугольной, если одна из боковых сторон перпендикулярна к основанию

Свойства параллелограмма Диагонали пересекаются и точкой пересечения делятся пополам.Противолежащие стороны – равны,

Свойства прямоугольника AC = BD.Все свойства параллелограммаЗадачи

Свойства ромба AC BD.AC – биссектриса A и

Свойства квадрата AC BD. AC = BD.AC – биссектриса

Признаки параллелограммаAB || CD, BC || ADЗадачи

Признаки ромбаABCD – параллелограмм,AB = BC = CD = DAЗадачи

Признаки квадратаABCD – параллелограмм,AB = BC = CD = DAКвадрат

Свойства параллелограмма. Задачи 1) MNKP — параллелограмм, МТ — биссектриса угла NMP,

Признаки параллелограмма. Задачи На рисунке ABCD — параллелограмм, BT = DK. Докажите, что АТСК—параллелограмм.Параллелограмм

Свойства прямоугольника. Задачи 1) В прямоугольнике ABCD угол BAC = 35°.

Свойства и признаки ромба. ЗадачиРомб1) В ромбе ABCD А = 36°.

Свойства и признаки квадрата. Задачи КвадратВнутри квадрата ABCD взята точка K и

Слайды презентации

Слайд 2 Цель – систематизировать свойства и признаки четырехугольников, изученные

на уроках геометрии

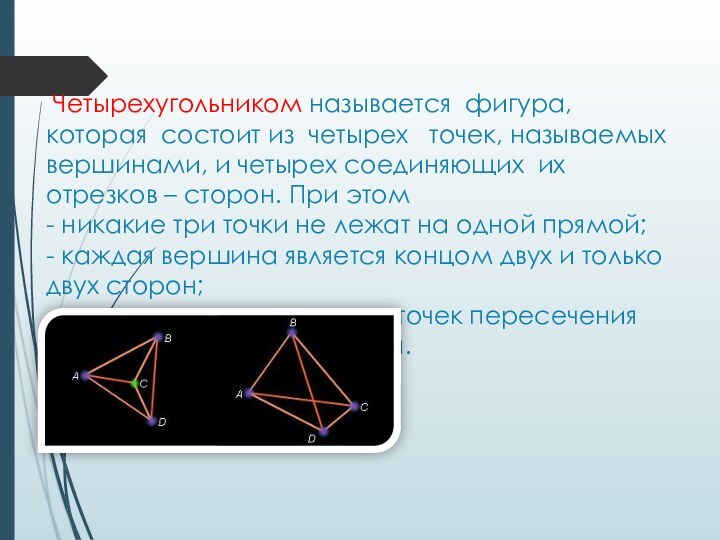
Слайд 3 Четырехугольником называется фигура, которая состоит из четырех

Четырехугольником называется фигура, которая состоит из четырех точек, называемых вершинами,

точек, называемых вершинами, и четырех соединяющих их отрезков

– сторон. При этом - никакие три точки не лежат на одной прямой; - каждая вершина является концом двух и только двух сторон; - стороны не имеют других точек пересечения кроме, может быть, вершин.

Слайд 4 Смежными являются стороны: [AB] и [CB], [BC] и

Смежными являются стороны: [AB] и [CB], [BC] и [CD], [CD] и

[CD], [CD] и [AD], [AB] и [AD].
Каждая пара:

[AB] и [CD], [BC] и [AD] – содержит противолежащие стороны.
Четыре пары вершин: A и B, B и C, C и D, A и D – содержат все возможные соседние вершины четырехугольника.
Пара вершин A и C (B и D ) являются противолежащими.

Стороны, исходящие из одной вершины, называются смежными.
Вершины, являющиеся концами одной стороны, называются соседними. Стороны, не имеющие общих вершин, называются противолежащими. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины, называются диагоналями.

Слайд 5

Слайд 6 Параллелограмм
Четырехугольник, у которого противоположные стороны параллельны, называется параллелограммом
Свойства
Признаки

Слайд 7 Параллелограмм
Четырехугольник, у которого противоположные стороны параллельны, называется параллелограммом
Свойства
Признаки

Слайд 8 Прямоугольник
Параллелограмм, у которого все углы прямые, называется

прямоугольником
Свойства
Признаки

Слайд 9 Прямоугольник
Параллелограмм, у которого все углы прямые, называется

прямоугольником
Свойства
Признаки

Слайд 10 Ромб
Параллелограмм, у которого все стороны равны, называется

ромбом
Свойства
Признаки

Слайд 11 Ромб
Параллелограмм, у которого все стороны равны, называется

ромбом
Свойства
Признаки

Слайд 12 Квадрат
Ромб, у которого все углы прямые, называется

квадратом
Свойства
Признаки

Слайд 13 Квадрат
Ромб, у которого все углы прямые, называется

квадратом
Свойства
Признаки

Слайд 14 Трапеция
Четырехугольник, у которого две противоположные стороны параллельны, а

две другие – непараллельные, называется трапецией

Слайд 15 Трапеция
Трапеция называется равнобедренной, если ее боковые стороны равны.
Верхнее

основание
Нижнее основание
Средняя линия

Слайд 16 Трапеция – называется прямоугольной, если одна из боковых

сторон перпендикулярна к основанию

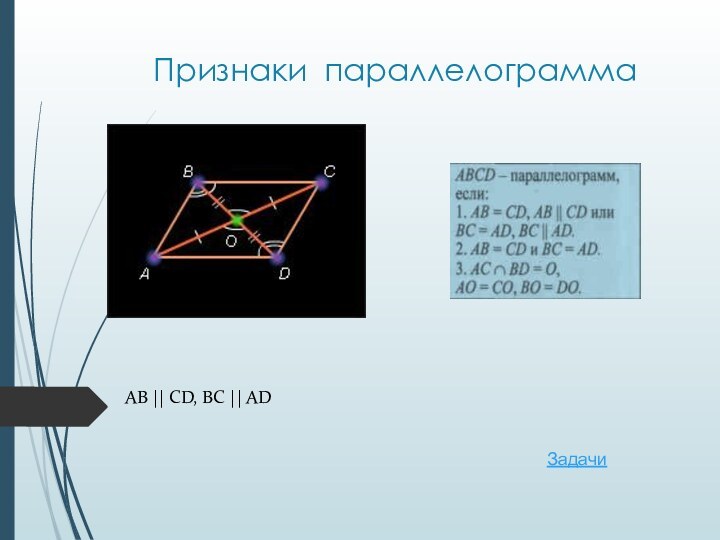
Слайд 17 Свойства параллелограмма
Диагонали пересекаются и точкой пересечения делятся

Свойства параллелограмма Диагонали пересекаются и точкой пересечения делятся пополам.Противолежащие стороны –

пополам.
Противолежащие стороны – равны, противолежащие углы равны.
Сумма односторонних углов

равна 180°.

AB || CD, BC || AD

Задачи

Слайд 18 Свойства прямоугольника
AC = BD.
Все свойства параллелограмма
Задачи

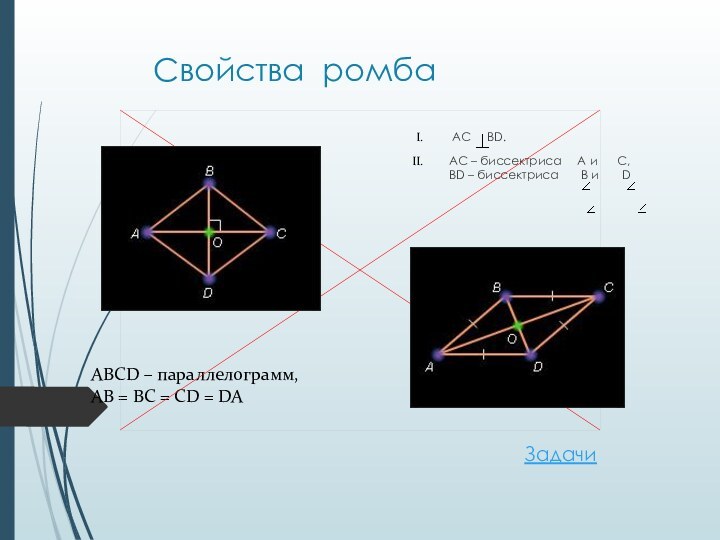
Слайд 19 Свойства ромба
AC BD.
AC – биссектриса

A и C, BD –

биссектриса B и D

ABCD – параллелограмм,
AB = BC = CD = DA

Задачи

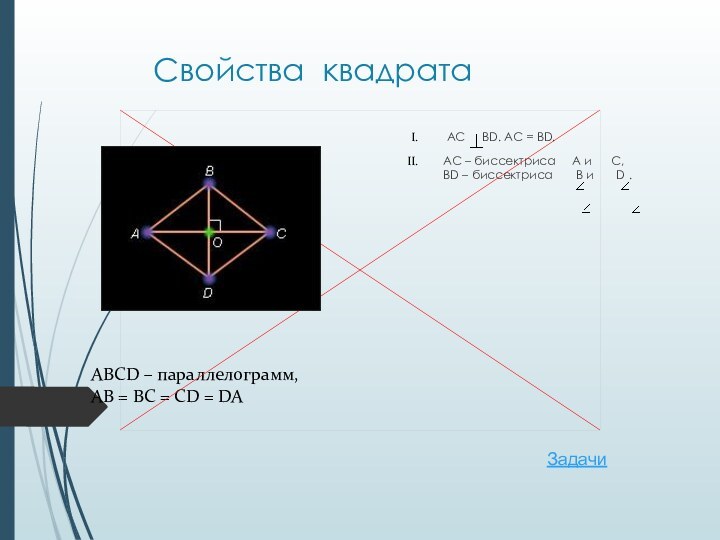
Слайд 20 Свойства квадрата
AC BD. AC =

BD.
AC – биссектриса A и

C, BD – биссектриса B и D .

ABCD – параллелограмм,
AB = BC = CD = DA

Задачи

Слайд 21 Признаки параллелограмма
AB || CD, BC || AD
Задачи

Слайд 22 Признаки прямоугольника
Прямоугольник

Слайд 23 Признаки ромба
ABCD – параллелограмм,
AB = BC = CD

= DA
Задачи

Слайд 24 Признаки квадрата
ABCD – параллелограмм,
AB = BC = CD

= DA
Квадрат

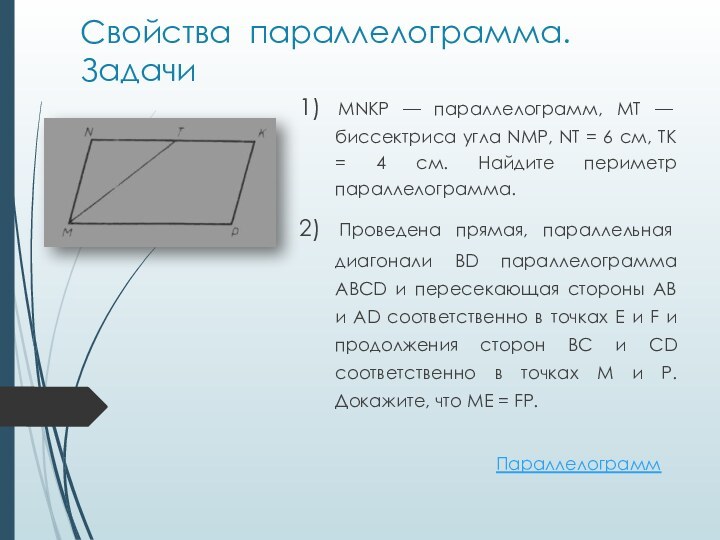
Слайд 25 Свойства параллелограмма. Задачи
1) MNKP — параллелограмм, МТ

Свойства параллелограмма. Задачи 1) MNKP — параллелограмм, МТ — биссектриса угла

— биссектриса угла NMP, NT = 6 см, ТК

= 4 см. Найдите периметр параллелограмма.
2) Проведена прямая, параллельная диагонали BD параллелограмма ABCD и пересекающая стороны АВ и AD соответственно в точках Е и F и продолжения сторон ВС и CD соответственно в точках М и Р. Докажите, что ME = FP.

Параллелограмм

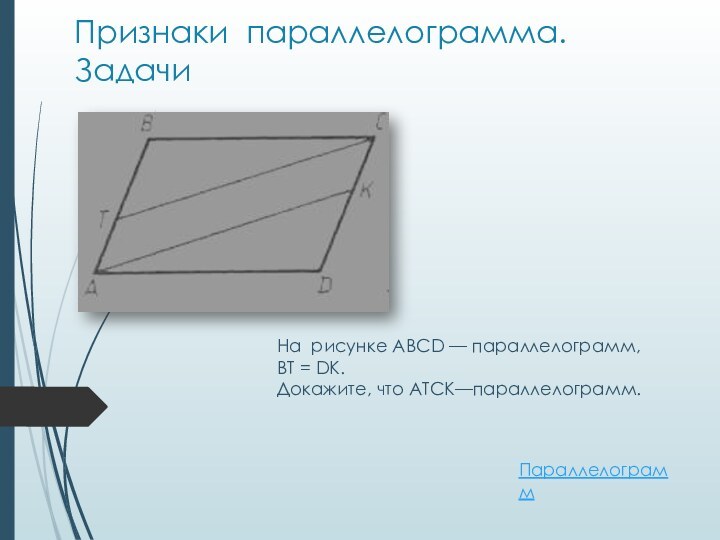
Слайд 26 Признаки параллелограмма. Задачи
На рисунке ABCD — параллелограмм,

BT = DK. Докажите, что АТСК—параллелограмм.
Параллелограмм

Слайд 27 Свойства прямоугольника. Задачи
1) В прямоугольнике ABCD

угол BAC = 35°. Найдите угол между диагоналями прямоугольника.

2) Постройте прямоугольник по диагонали и углу между диагоналями.

Прямоугольник

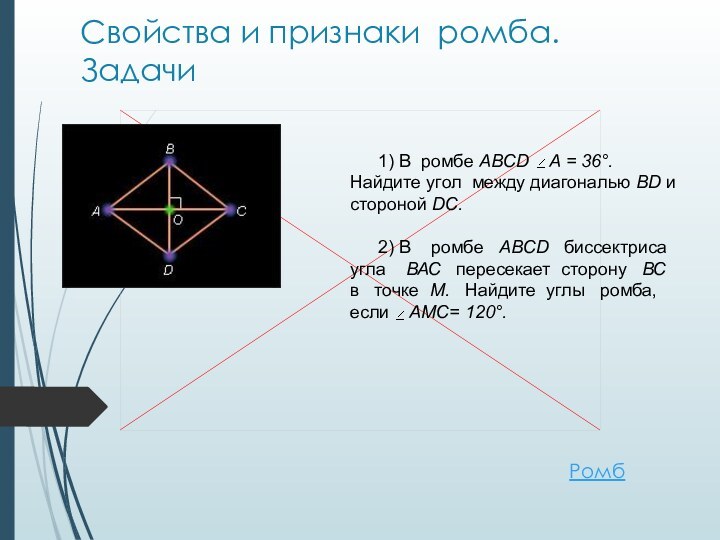
Слайд 28 Свойства и признаки ромба. Задачи
Ромб
1) В ромбе ABCD

А = 36°. Найдите угол между диагональю BD

и стороной DC.

2) В ромбе ABCD биссектриса угла ВАС пересекает сторону ВС в точке М. Найдите углы ромба, если АМС= 120°.

Слайд 29 Свойства и признаки квадрата. Задачи
Квадрат
Внутри квадрата ABCD

Свойства и признаки квадрата. Задачи КвадратВнутри квадрата ABCD взята точка K

взята точка K и на отрезке АК как на

стороне построен квадрат AKLM, у которого сторона KL пересекает сторону AD. Докажите, что отрезки ВК и DM равны.

2) ABCD — квадрат, точка М принадлежит стороне CD, АК — биссектриса угла ВАМ (К ВС). Докажите, что AM = BK + DM.