- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Объем конуса
Содержание
- 2. ОБЪЕМ КОНУСА В частности, для кругового конуса,
- 3. ОБЪЕМ УСЕЧЕННОГО КОНУСАПолученное при этом сечение конуса
- 4. ОБЪЕМ УСЕЧЕННОГО КОНУСАОбъем усеченного конуса, основания которого
- 5. Упражнение 1Во сколько раз увеличится объем кругового
- 6. Упражнение 2Изменится ли объем кругового конуса, если
- 7. Упражнение 3Цилиндр и конус имеют общее основание
- 8. Упражнение 4Объем конуса равен 1. Параллельно основанию
- 9. Упражнение 5Высота конуса 3 см, образующая 5 см. Найдите его объем.
- 10. Упражнение 6Диаметр основания конуса равен 12 см,
- 11. Упражнение 7Найдите объем тела, получающегося при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 3 см.
- 12. Упражнение 8Равносторонний треугольник вращается вокруг своей стороны, равной 1. Найдите объем тела вращения.
- 13. Упражнение 9Равнобедренная трапеция, основания которой равны 4
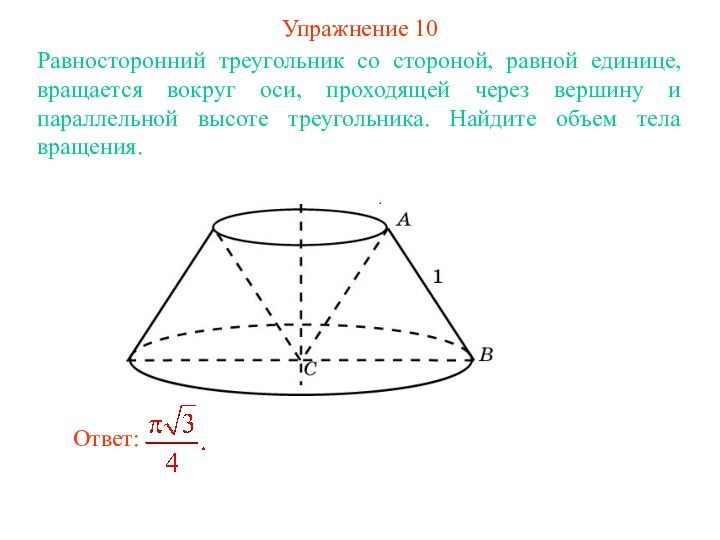
- 14. Упражнение 10Равносторонний треугольник со стороной, равной единице,
- 15. Упражнение 11Конус вписан в правильную треугольную пирамиду
- 16. Упражнение 12Конус описан около правильной четырехугольной пирамиды
- 17. Упражнение 13Радиусы оснований усеченного конуса равны 1
- 18. Упражнение 14Объем усеченного конуса равен 584π см3,
- 19. Упражнение 15Усеченный конус, у которого радиусы оснований
- 20. Упражнение 16На меньшем основании усеченного конуса построен
- 21. Упражнение 17Объем конуса равен 1. Его высота
- 22. Упражнение 18Высота усеченного конуса равна 3. Радиус
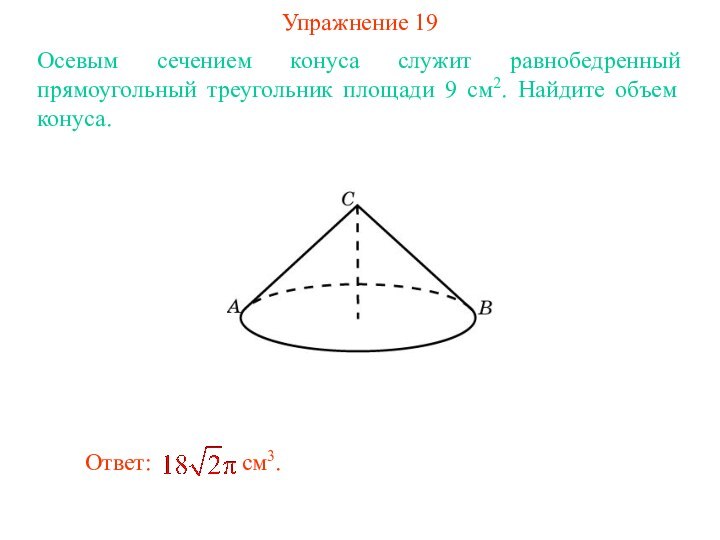
- 23. Упражнение 19Осевым сечением конуса служит равнобедренный прямоугольный треугольник площади 9 см2. Найдите объем конуса.
- 24. Упражнение 20Радиусы оснований усеченного конуса равны 3
- 25. Упражнение 21Два конуса имеют общую высоту и
- 26. Упражнение 22Разверткой боковой поверхности конуса служит полукруг радиуса 2. Найдите объем конуса.
- 27. Скачать презентацию
- 28. Похожие презентации
ОБЪЕМ КОНУСА В частности, для кругового конуса, в основании которого – круг радиуса R, и высота которого равна h, имеет место формула
























Слайд 3
ОБЪЕМ УСЕЧЕННОГО КОНУСА
Полученное при этом сечение конуса также
называется основанием усеченного конуса. Расстояние между плоскостями оснований называется
высотой усеченного конуса.Для данного конуса рассмотрим плоскость, параллельную основанию и пересекающую конус. Часть конуса, заключенная между этой плоскостью и основанием, называется усеченным конусом.
Теорема. Объем усеченного конуса выражается формулой
где S, s - площади оснований, g - высота усеченного конуса.
Слайд 4
ОБЪЕМ УСЕЧЕННОГО КОНУСА
Объем усеченного конуса, основания которого –
круги радиусов R и r, а высота равна h,
выражается формулой
Слайд 5
Упражнение 1
Во сколько раз увеличится объем кругового конуса,
если: а) высоту увеличить в 3 раза; б) радиус
основания увеличить в 2 раза?Ответ: а) В 3 раза; б) в 4 раза.
Слайд 6
Упражнение 2
Изменится ли объем кругового конуса, если радиус
основания увеличить в 2 раза, а высоту уменьшить в
2 раза?Ответ: Увеличится в 2 раза.
Слайд 7
Упражнение 3
Цилиндр и конус имеют общее основание и
высоту. Вычислите объем цилиндра, если объем конуса равен 40
π см3.Ответ: 120 см3.
Слайд 8
Упражнение 4
Объем конуса равен 1. Параллельно основанию конуса
проведено сечение, делящее высоту пополам. В каком отношении находятся
объемы полученных частей конуса?Ответ: 1:7.
Слайд 10
Упражнение 6
Диаметр основания конуса равен 12 см, а
угол при вершине осевого сечения - 90°. Вычислите объем
конуса.
Слайд 11
Упражнение 7
Найдите объем тела, получающегося при вращении равнобедренного
прямоугольного треугольника вокруг катета, равного 3 см.
Слайд 12
Упражнение 8
Равносторонний треугольник вращается вокруг своей стороны, равной
1. Найдите объем тела вращения.
Слайд 13
Упражнение 9
Равнобедренная трапеция, основания которой равны 4 см
и 6 см, а высота – 3 см, вращается
относительно оси симметрии. Найдите объем тела вращения.
Слайд 14
Упражнение 10
Равносторонний треугольник со стороной, равной единице, вращается
вокруг оси, проходящей через вершину и параллельной высоте треугольника.
Найдите объем тела вращения.
Слайд 15
Упражнение 11
Конус вписан в правильную треугольную пирамиду со
стороной основания 1 и высотой 2. Найдите его объем.
Слайд 16
Упражнение 12
Конус описан около правильной четырехугольной пирамиды со
стороной основания a и высотой h. Найдите его объем.
Слайд 17
Упражнение 13
Радиусы оснований усеченного конуса равны 1 и
2. Образующая наклонена к основанию под углом 45о. Найдите
его объем.
Слайд 18
Упражнение 14
Объем усеченного конуса равен 584π см3, а
радиусы оснований 10 см и 7 см. Найдите высоту
усеченного конуса.Ответ: 8 см.
Слайд 19
Упражнение 15
Усеченный конус, у которого радиусы оснований 3
см и 5 см, и полный конус такой же
высоты равновелики. Чему равен радиус основания полного конуса?Ответ: 7 см.
Слайд 20
Упражнение 16
На меньшем основании усеченного конуса построен цилиндр,
второе основание которого лежит в плоскости большего основания. Объем
цилиндра составляет седьмую часть объема усеченного конуса. Найдите зависимость между радиусами оснований усеченного конуса.Ответ: R = 4r.
Слайд 21
Упражнение 17
Объем конуса равен 1. Его высота разделена
на три равные части, и через точки деления параллельно
основанию проведены плоскости. Найдите объем средней части конуса.
Слайд 22
Упражнение 18
Высота усеченного конуса равна 3. Радиус одного
основания вдвое большее другого, а образующая наклонена к основанию
под углом 45°. Найдите объем.
Слайд 23
Упражнение 19
Осевым сечением конуса служит равнобедренный прямоугольный треугольник
площади 9 см2. Найдите объем конуса.
Слайд 24
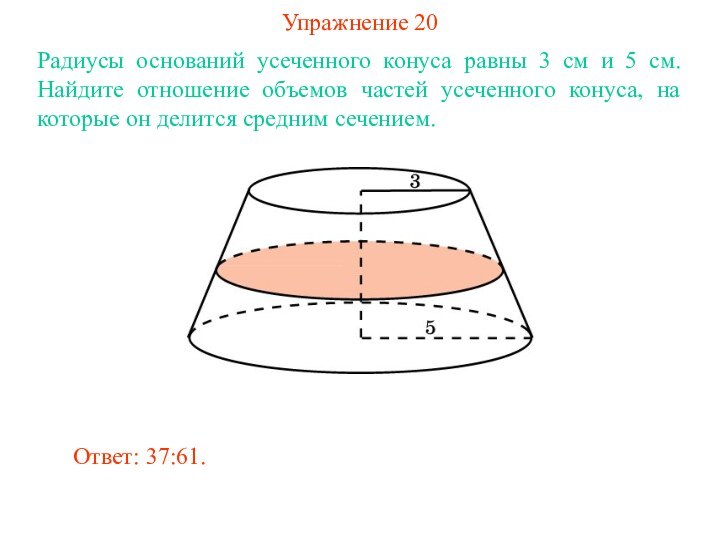
Упражнение 20
Радиусы оснований усеченного конуса равны 3 см
и 5 см. Найдите отношение объемов частей усеченного конуса,
на которые он делится средним сечением.Ответ: 37:61.
Слайд 25
Упражнение 21
Два конуса имеют общую высоту и параллельные
основания. Найдите объем их общей части, если объем каждого
конуса равен 1.Ответ: