Слайд 2
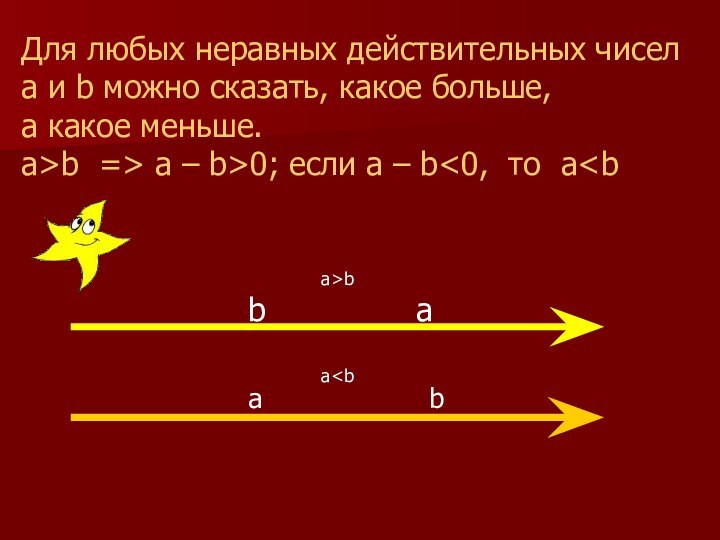
Для любых неравных действительных чисел
a и b можно
сказать, какое больше,
а какое меньше.
a>b => a –
b>0; если a – b<0, то a
a
b
a
b
a>b
a
Слайд 3
Знаки неравенств
Строгие неравенства:
A>B, 67>35
d
Р, Е больше или равно Р
(Е не меньше
Р);
К ≤ М, К меньше или равно М
(К не больше М).
Слайд 4
Двойные неравенства:
Двойное неравенство a < b < c
верно, если одновременно верны два неравенства a < b
и b < c, и неверно в противном случае.
Двойное неравенство d > e > f верно, если …
Слайд 8
Свойство 1.
Если aa; если а>b, то
b
число. Тогда b – a - положительное число, т.е. b>a.
Наоборот, если a>b, то…
Слайд 9
Свойство 2.
Если a
разности а – с приба-
вим числа b и –b
и сгруппируем слагаемые: a – c = a – c + b – b =(a –
-b) + (b – c).
Посмотрите на условие и сделайте вывод.
Слайд 10
Свойство 3.
Если a
число, то а + с
(а + с) – (b + c)=…
Раскройте скобки, упростите и сделайте вывод.
Если к обеим частям верного неравенства прибавить одно и то же число, то…
Слайд 11
Следствие
Любое число можно перенести из одной части неравенства
в другую с противоположным знаком.
Слайд 12
Свойство 4.
Если a
то ас
то ac>bc.
Доказательство. Рассмотрите разность
ас – bc = c(a – b) и сделайте выводы.
Слайд 13
Выводы:
Если обе части верного неравенства умножить на одно
и то же положительное число и сохранить знак исходного
неравенства, то получится верное неравенство;
Если обе части верного неравенства умножить на отрицательное число, то знак неравенства нужно поменять на противоположный.
Слайд 14
Следствие.
Если а и b – положительные числа и
а
число ab и, сократив дроби, посмотрим на результат.
Слайд 15
Свойство 5.
Если a
с
+ c; cb + cа теперь посмотрите свойство 2.
Если сложить почленно два верных неравенства одного знака и знак неравенства сохранить, то получим…
Слайд 16
Свойство 6.
Если ad, то a –
cd, то – с
d. Но по свойству 5: a < b
+
-c < - d
----------------
a – c < b – d ч.т.д.
Слайд 17
Вывод:
Два верных неравенства противоположного знака
можно почленно вычитать,
оставляя знак того неравенства,
из которого вычитали
другое неравенство.
Слайд 18
Свойство 7
Если a,b,c,d – положительные числа, a
то ac
ac0, следовательно bcСмотрим второе свойство и делаем вывод!
Слайд 19
Итак,
Если перемножить почленно
два верных неравенства одного знака,
левые и правые части которых положительные числа,
то получится верное
неравенство,
имеющее тот же знак,
что и данное неравенство.
Слайд 20
Следсвия из седьмого свойства:
Следствие 1. Если 0
2. Если 0