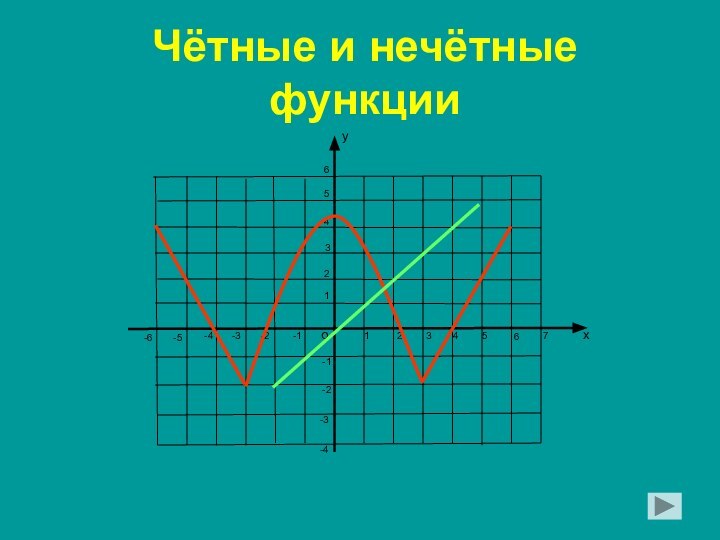
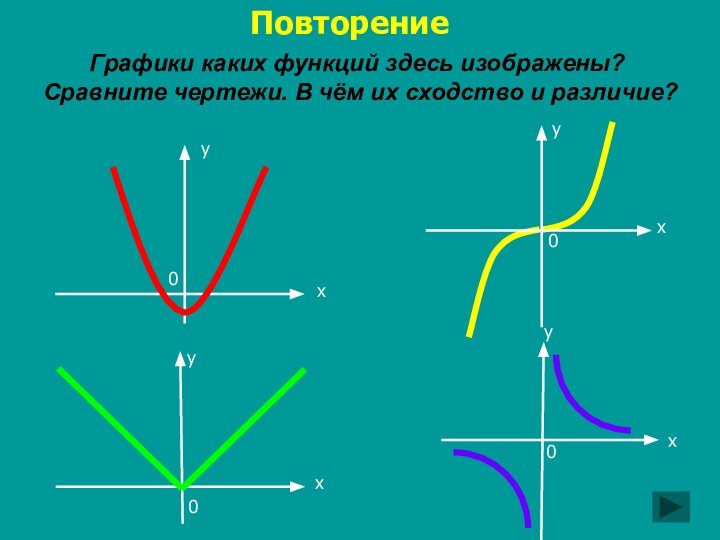
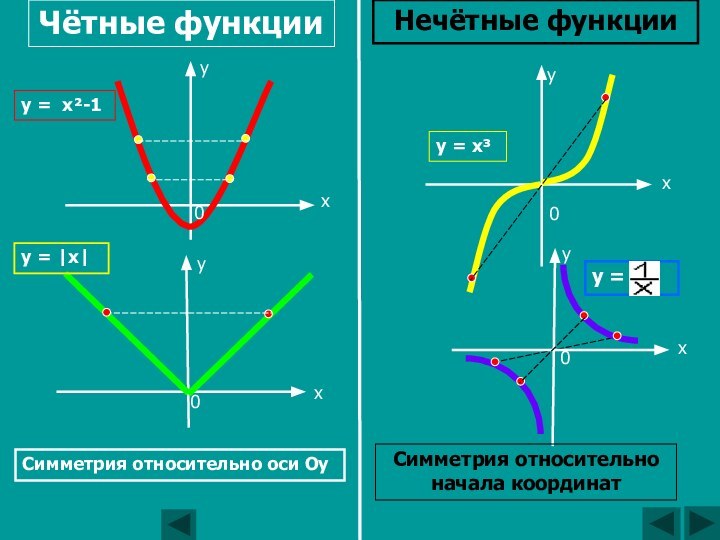
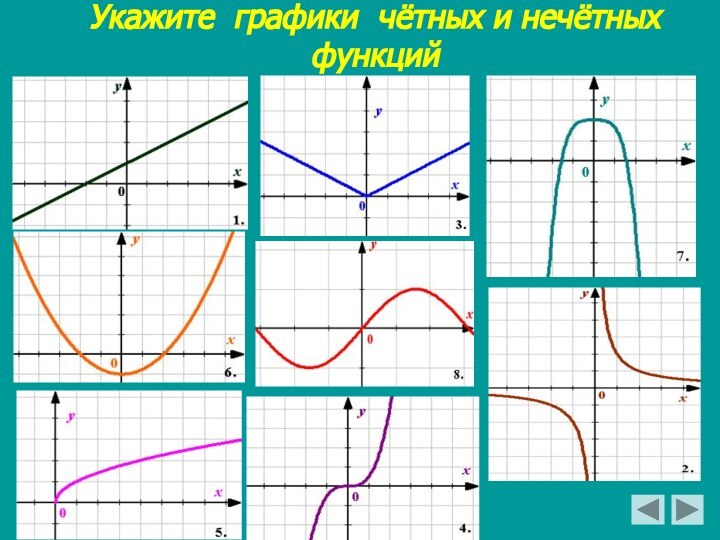
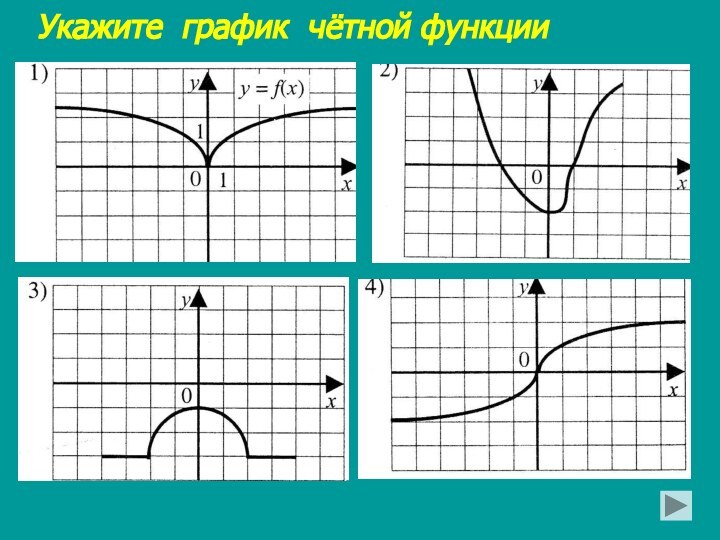
относительно нуля;
2) для любого х Є D (f)
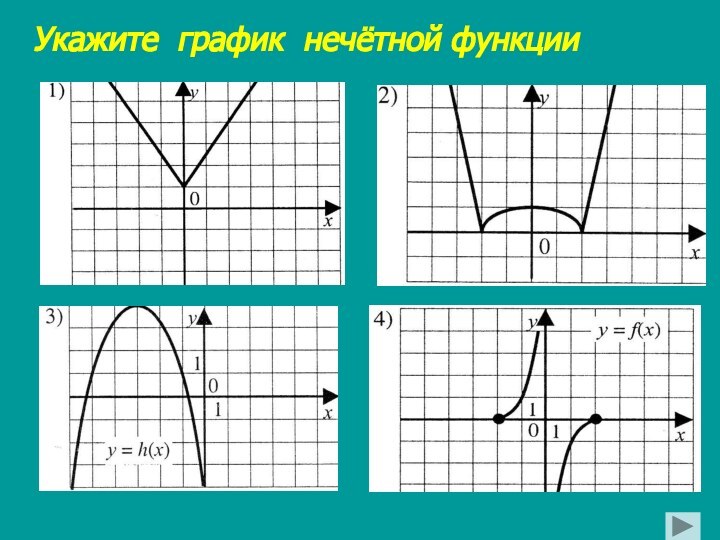
верно равенство: f (-x) = f (x).Функция y=f (x) называется нечётной, если:
1) D (f) симметрична относительно нуля;
2) для любого х Є D (f) верно равенство: f (-x) = - f (x).
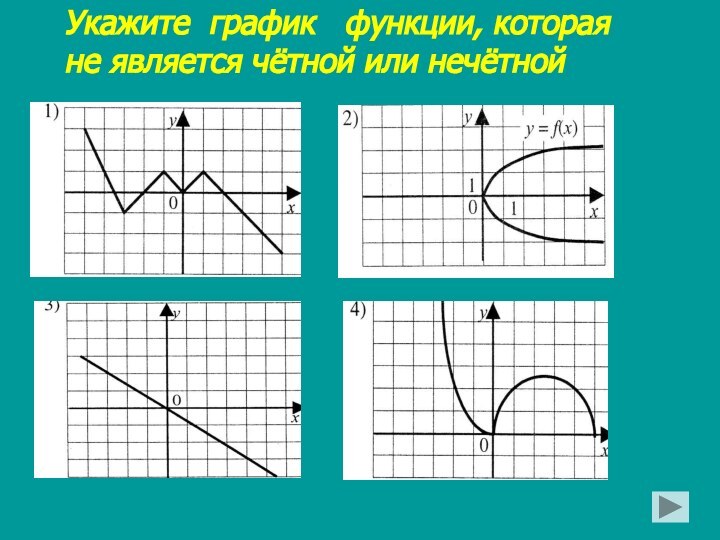
Выяснить является ли функция чётной или нечётной:
y (х) = 5 x²- |X|
Решение: D (y) = R
y (- x)=
=5 (- x)² - |- x| =
= 5 x² - |x|=
= y (x)
Значит, функция - чётная
у(х) = 7x +x³
Решение: D (y) = R
y (- x)=
= 7(- x) +(- x)³=
= - 7 x - x³ =
= - (7x +x³)
= - y (x)
Значит, функция - нечётная