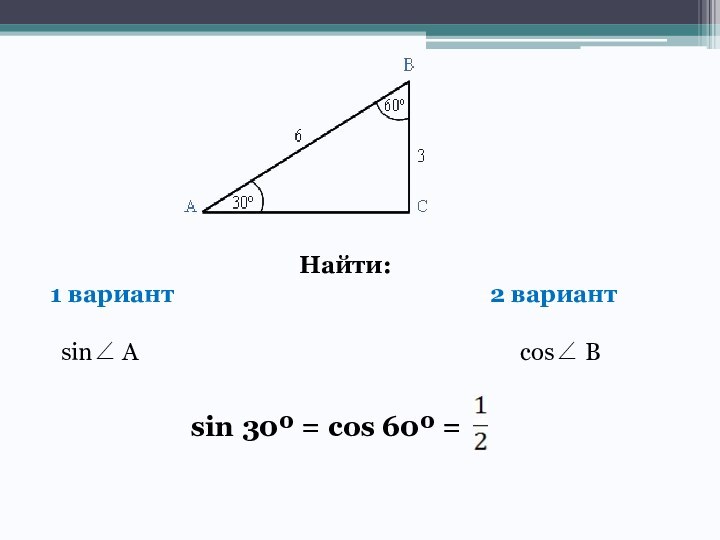
Найти:
1 вариант 2 вариант
sin A cos B
sin 30º = cos 60º =
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Синус, косинус и тангенс угла
Содержание
- 3. Единичная полуокружность Определение. Полуокружность называется единичной, если
- 4. Синус, косинус, тангенс углаСинус угла – ордината
- 5. Синус, косинус, тангенс углаТак как координаты (х;
- 6. Значения синуса и косинуса для углов 0,
- 7. Т.к. tg = , то
- 8. Тригонометрическая таблица
- 9. Основное тригонометрическое тождествоУравнение окружностих2 + у2 =
- 10. Знаки синуса, косинуса, тангенса, катангенсаsin =
- 11. Формулы приведенияsin (90 - ) = cos
- 12. Формулы для вычисления координат точкиМ(сosα; sinα). А
- 13. Домашнее задание§1, пп. 93 - 95, №№ 1014, 1015 (б, г)
- 14. Урок оконченДо свидания!
- 15. Скачать презентацию
- 16. Похожие презентации
Найти: 1 вариант
Слайд 3
Единичная полуокружность
Определение. Полуокружность называется единичной, если ее
центр находится в начале координат, а радиус равен 1.
Слайд 4
Синус, косинус,
тангенс угла
Синус угла – ордината у
точки М
sin = , MD
= y, sin = y.Косинус угла – абсцисса х точки М
cos = , OD = x, cos = x.
Тангенс, катангенс угла
Т. к. tg = , tg = , ctg =
0 ≤ ≤ 180
Слайд 5
Синус, косинус,
тангенс угла
Так как координаты (х; у)
заключены в промежутках
0 ≤ у ≤ 1, -
1 ≤ х ≤ 1,то для любого из промежутка
0 ≤ ≤ 180
справедливы неравенства:
0 ≤ sin ≤ 1,
- 1≤ cos ≤ 1
Слайд 6
Значения синуса и косинуса
для углов 0, 90
и 180
Так как точки А, С и B имеют
координаты А (1; 0), С (0; 1), В (-1; 0), то
sin 0 = 0,
sin 90 = 1,
sin 180 = 0,
cos 0 = 1,
cos 90 = 0,
cos 180 = - 1
Слайд 7 Т.к. tg = , то при
= 90 тангенс угла не определен.
tg
0 = 0, tg 180 = 0.Т.к. ctg = , то при = 0, = 180 катангенс угла не определен
ctg 90 = 0.
Значения тангенса и катангенса
0, 90 и 180
Слайд 9
Основное тригонометрическое
тождество
Уравнение окружности
х2 + у2 = 1
sin
= x, cos = y
0 ≤ ≤ 180
sin2
+ cos2 = 1
Слайд 10
Знаки синуса, косинуса,
тангенса, катангенса
sin =
I , II ч - sin >
0, III, IV ч - sin <0cos =
I , IV ч - cos > 0, II, III ч - cos <0
tg =
I , III ч - tg > 0, II, IV ч - tg <0
ctg =
I , III ч - ctg > 0, II, IV ч - ctg <0
Слайд 11
Формулы приведения
sin (90 - ) = cos
cos
(90 - ) = sin (5)
при 0 ≤ ≤ 90,sin (180 - )= sin
cos (180 - ) = - cos (6) при 0 ≤ ≤ 180
Слайд 12
Формулы для вычисления
координат точки
М(сosα; sinα). А (
x;y) – произвольная точка
sin = y, cos
= x М(cos ; sin ), (cos ; sin ), (х;у)
По лемме о коллинеарных векторах
= ОА∙ , поэтому
x = ОА ∙ cos ,
y = OA ∙ sin .
