- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Длина окружности
Содержание
- 2. Представим. Что мы разрезаем окружность и «распрямляем»
- 3. Представим. Что мы разрезаем окружность и «распрямляем»
- 5. n = 4
- 6. n = 6
- 7. n = 8
- 10. История числа пи началась в Древнем Египте.
- 11. Архимед в III в. до н.э. обосновал в своей
- 12. В первой половине XV в. обсерватории Улугбека,
- 13. Первым ввёл обозначение отношения длины окружности к
- 14. Историческая справкаЕщё древние греки знали одно замечательное
- 15. Интересные факты Отношение длины основания Великой
- 16. Интересные факты Лидером по тупым законам
- 17. Интересные факты Помните бородатый анекдот про школьного
- 18. Интересные факты Во времена развитого социализма
- 19. где - градусная
- 20. Скачать презентацию
- 21. Похожие презентации
Представим. Что мы разрезаем окружность и «распрямляем» ее в нить.Длина получившегося в этом случае отрезка и есть длина окружности.



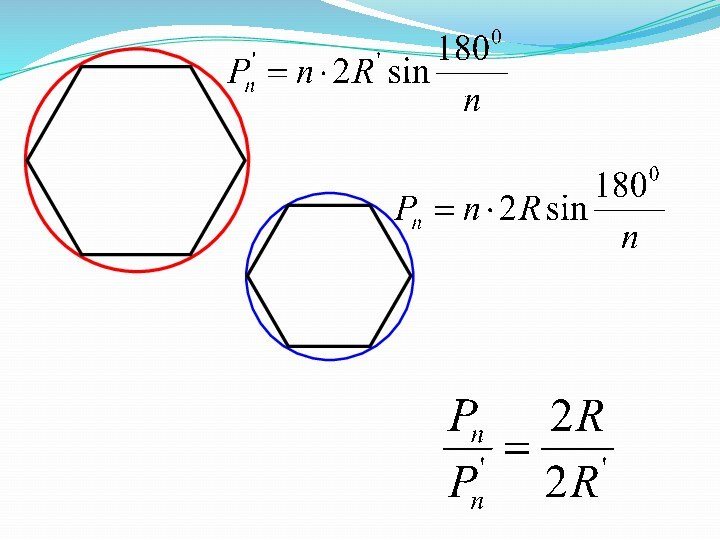

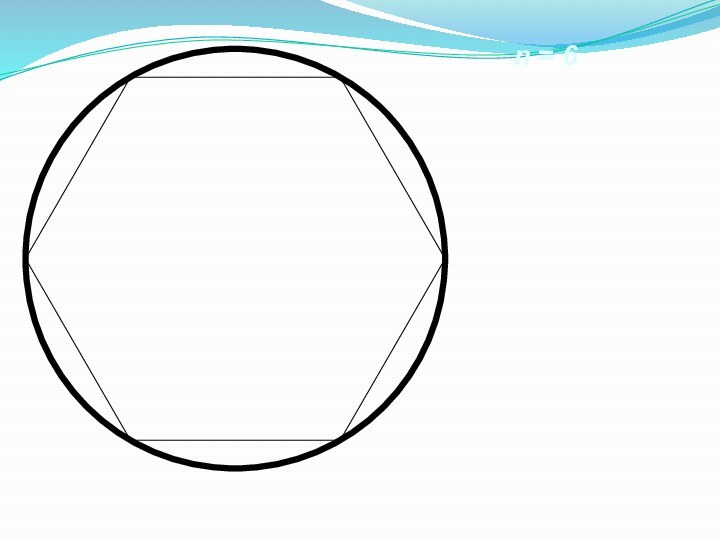

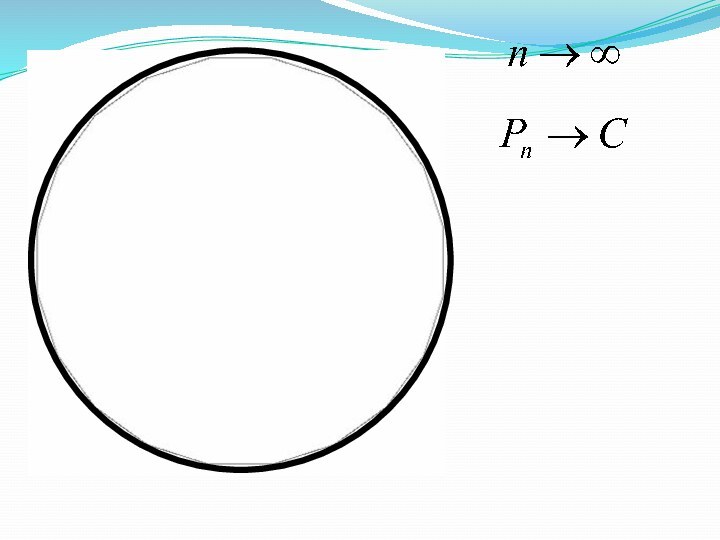












Слайд 3 Представим. Что мы разрезаем окружность и «распрямляем» ее
в нить.
Длина получившегося в этом случае отрезка и есть
длина окружности.Длина окружности обозначается буквой C.
Слайд 10 История числа пи началась в Древнем Египте. Площадь
круга диаметром d египетские математики определяли как (d-d/9)2, т.е.
в древнем ЕгиптеВ священной книге джайнизма (одной из древнейших религий, существовавших в Индии и возникшей в VI в. до н.э.) имеется указание, из которого следует, что число пи в то время принимали равным , что даёт дробь 3,162...
Слайд 11 Архимед в III в. до н.э. обосновал в своей небольшой
работе "Измерение круга" три положения:
всякий круг равновелик прямоугольному
треугольнику, катеты которого соответственно равны длине окружности и её радиусу;
площади круга относятся к квадрату, построенному на диаметре, как 11 к 14;
отношение любой окружности к её
диаметру меньше 3 1/7 и больше 3 10/71.
Слайд 12 В первой половине XV в. обсерватории Улугбека, возле
Самарканда, астроном и математик ал-Каши вычислил "пи" с 16
десятичными знаками. Он сделал 27 удвоений числа сторон многоугольников и дошёл до многоугольника, имеющего 3*228 углов. Ал-Каши произвёл уникальные расчёты, которые были нужны для составления таблицы синусов с шагом в 1'. Эти таблицы сыграливажную роль в астрономии.
Только через 250 лет после ал-Каши
его результат был превзойдён.
Слайд 13 Первым ввёл обозначение отношения длины окружности к диаметру
современным символом
английский математик У.Джонсон в 1706 г.
В качестве символа он взял первую букву греческого слова "periferia", что в переводе означает "окружность". Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь,
Чтобы нам не ошибаться,
Чтоб окружность верно счесть,
Надо только постараться
И запомнить все как есть
Три — четырнадцать — пятнадцать — девяносто два и шесть!..
Слайд 14
Историческая справка
Ещё древние греки знали одно замечательное свойство
круга: из всех фигур имеющих одинаковую длину периметра, наибольшую
площадь имеет круг.
Слайд 15
Интересные факты
Отношение длины основания Великой Пирамиды
к ее высоте, разделенное пополам, дает знаменитое число "пи"
.Возможно, оно намеренно зашифровано в размерах Пирамиды Хеопса, причем с более точным значением, чем его знал великий Архимед, живший позже на 2000 лет!