- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Движение и сопряжение линий
Содержание
- 2. Содержание Движениеа) Отображение плоскости на себяб)
- 3. ДвижениеОтображение плоскости на себя Любая точка плоскости оказывается
- 4. Понятие движенияЛюбое отображение, сохраняющее расстояния между
- 5. Осевая симметрияaАА1ось симметрииОсевая симметрия — вид движения, при
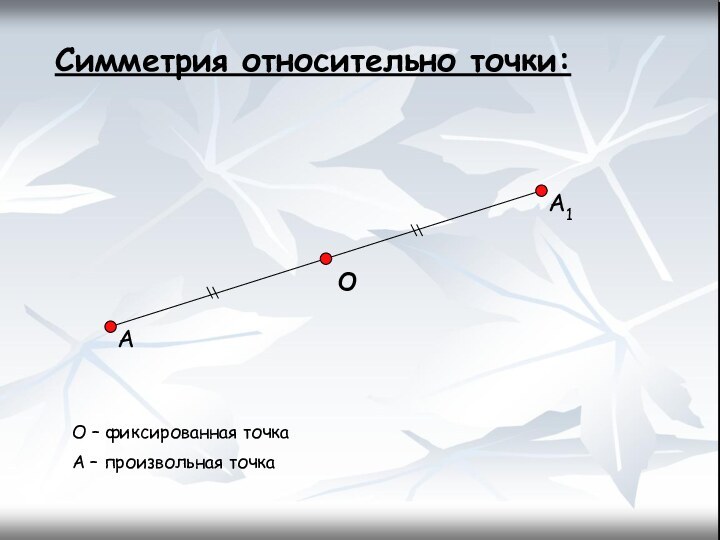
- 6. Симметрия относительно точки:О – фиксированная точка A – произвольная точка ОАА1
- 7. Параллельный переносПараллельным переносом на вектор а
- 8. Параллельный перенос треугольника на заданный вектор ааАВСС1А1В1Доказательство:
- 9. Параллельный перенос окружности на заданный вектор аОаО1Доказательство:Докажем,
- 10. Сопряжение Сопряжением называют плавный переход одной линии
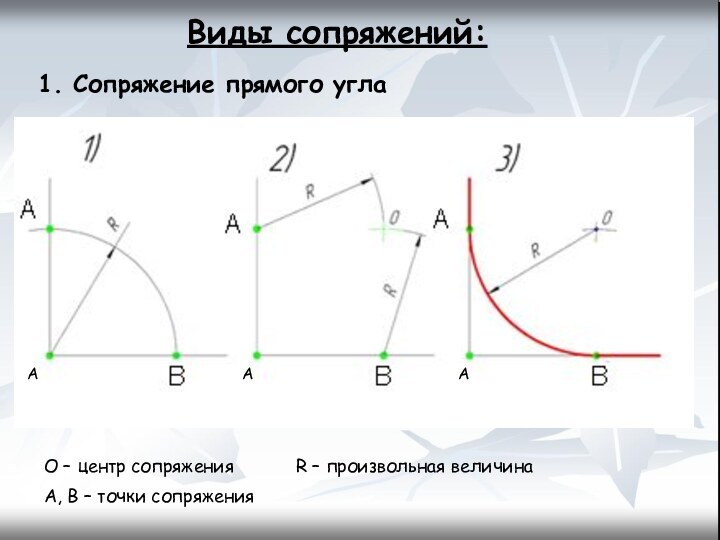
- 11. 1. Сопряжение прямого углаО – центр сопряжения R – произвольная величинаA, B – точки сопряженияВиды сопряжений:ААА
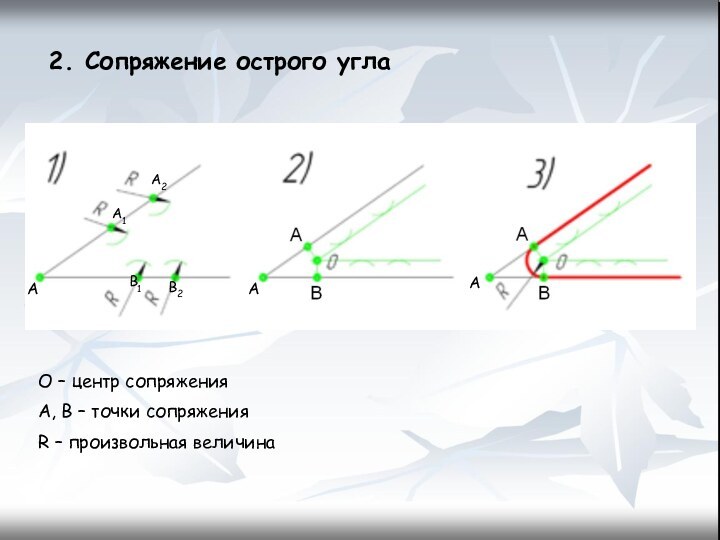
- 12. 2. Сопряжение острого углаО – центр сопряженияA, B – точки сопряженияR – произвольная величинаАААА1А2В1В2
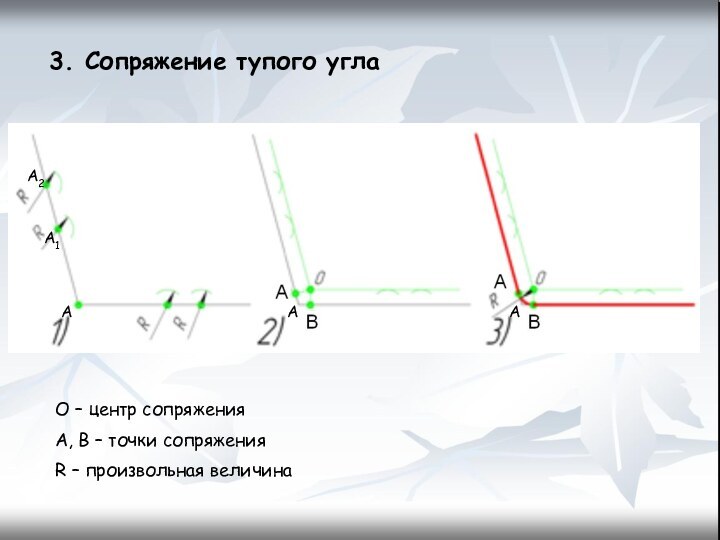
- 13. 3. Сопряжение тупого углаО – центр сопряженияA, B – точки сопряженияR – произвольная величинаАААА1А2
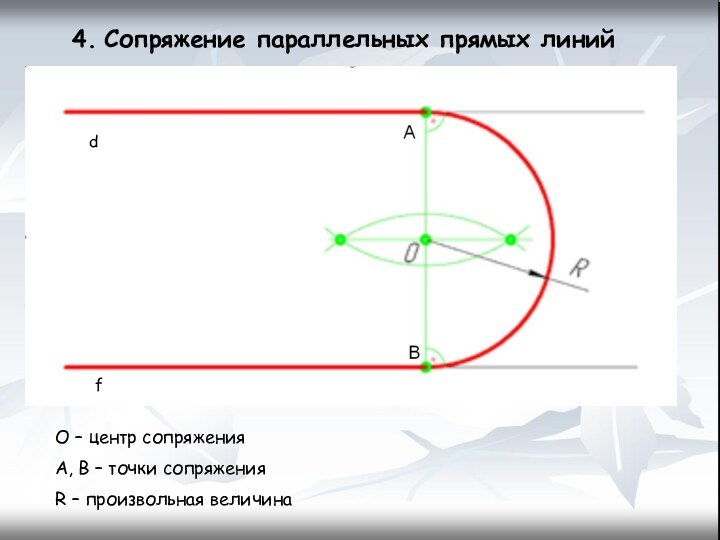
- 14. 4. Сопряжение параллельных прямых линийО – центр сопряженияA, B – точки сопряженияR – произвольная величинаdf
- 15. Скачать презентацию
- 16. Похожие презентации
Содержание Движениеа) Отображение плоскости на себяб) Понятие движенияв) Осевая симметрияг) Параллельный перенос Сопряжениеа) Понятие сопряжения б) Виды сопряжений




Слайд 3
Движение
Отображение плоскости на себя
Любая точка плоскости оказывается сопоставлена
некоторой точке. Говорят, что дано отображение плоскости на себя.
Слайд 4
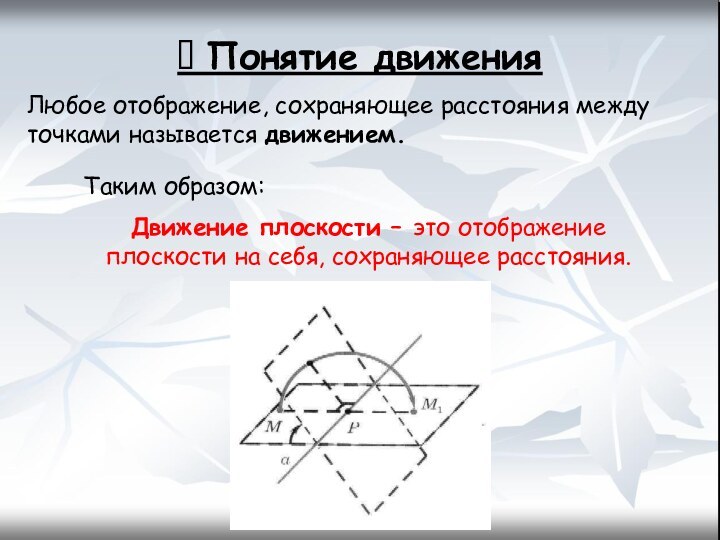
Понятие движения
Любое отображение, сохраняющее расстояния между точками
называется движением.
Таким образом:
Движение плоскости – это отображение плоскости
на себя, сохраняющее расстояния.
Слайд 5
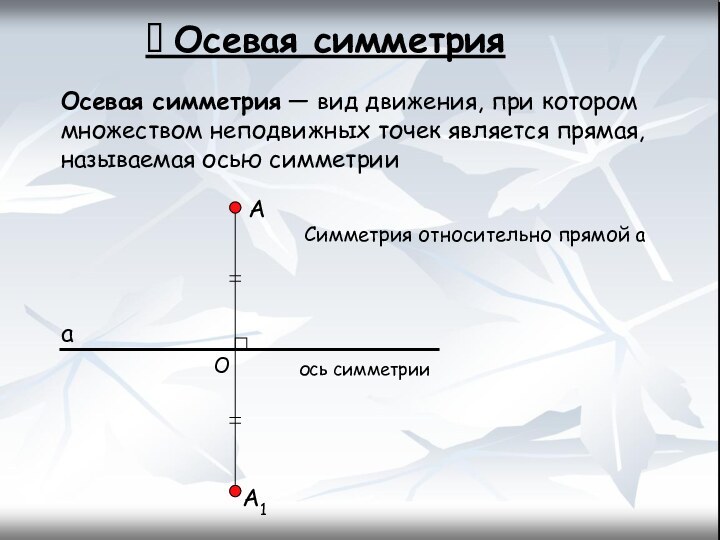
Осевая симметрия
a
А
А1
ось симметрии
Осевая симметрия — вид движения, при котором
множеством неподвижных точек является прямая, называемая осью симметрии
Симметрия относительно прямой а
О
Слайд 7
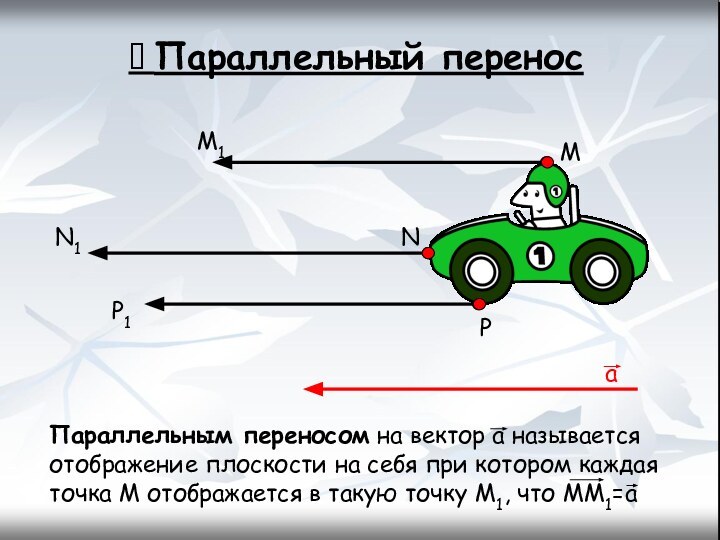
Параллельный перенос
Параллельным переносом на вектор а называется
отображение плоскости на себя при котором каждая точка М
отображается в такую точку М1, что ММ1=аМ
N
P
М1
N1
P1
a
Слайд 8
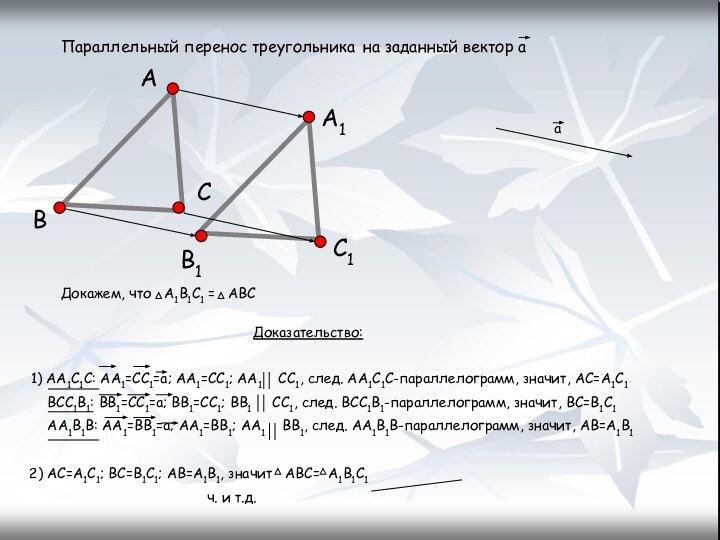
Параллельный перенос треугольника на заданный вектор а
а
А
В
С
С1
А1
В1
Доказательство:
1)
АА1С1С: АА1=СС1=а; АА1=СС1; АА1 СС1, след. АА1С1С-параллелограмм, значит,
АС=А1С1ВСС1В1: ВВ1=СС1=а; ВВ1=СС1; ВВ1 СС1, след. ВСС1В1-параллелограмм, значит, ВС=В1С1
АА1В1В: АА1=ВВ1=а; АА1=ВВ1; АА1 ВВ1, след. АА1В1В-параллелограмм, значит, АВ=А1В1
2) АС=А1С1; ВС=В1С1; АВ=А1В1, значит АВС= А1В1С1
ч. и т.д.
Докажем, что А1В1С1 = АВС
Слайд 9
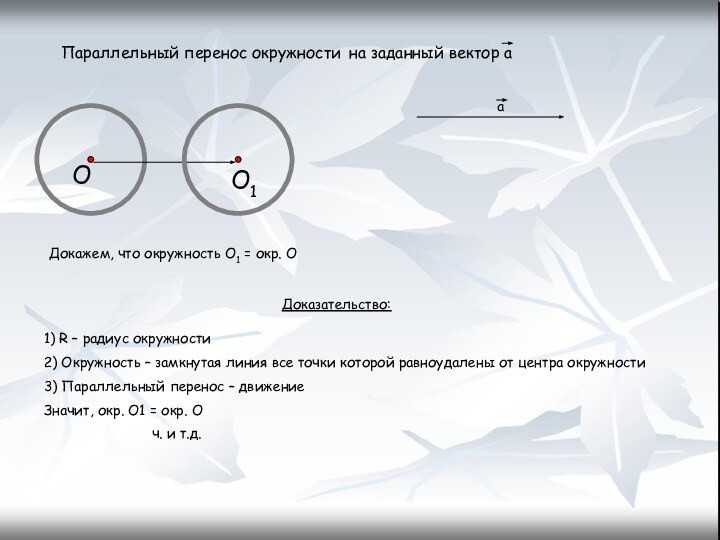
Параллельный перенос окружности на заданный вектор а
О
а
О1
Доказательство:
Докажем, что
окружность О1 = окр. О
1) R – радиус окружности
2)
Окружность – замкнутая линия все точки которой равноудалены от центра окружности3) Параллельный перенос – движение
Значит, окр. О1 = окр. О
ч. и т.д.
Слайд 10
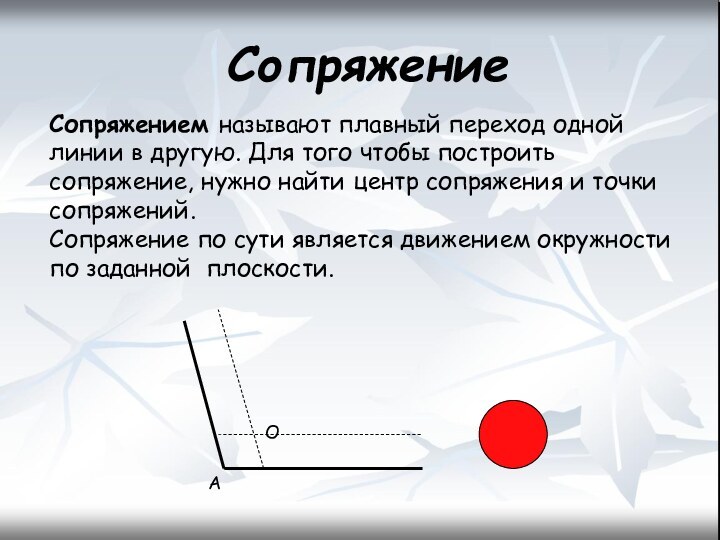
Сопряжение
Сопряжением называют плавный переход одной линии в
другую. Для того чтобы построить сопряжение, нужно найти центр
сопряжения и точки сопряжений.Сопряжение по сути является движением окружности по заданной плоскости.
О
А