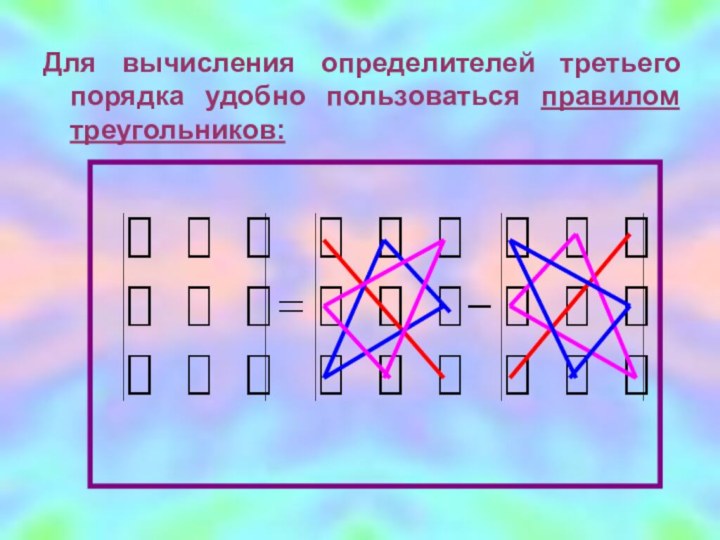
часто возникает необходимость вычислить определитель матрицы. Определитель матрицы используется
в линейной алгебре, аналитической геометрии, математическом анализе, поэтому без навыка решения определителей просто не обойтись.Цель работы: повторить правила и определить возможности упрощения вычислений определителей порядка выше третьего.