- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему двугранные углы
Содержание
- 2. ЦЕЛИ УРОКА:ВВЕСТИ ПОНЯТИЕ ДВУГРАННОГО УГЛА И ЕГО
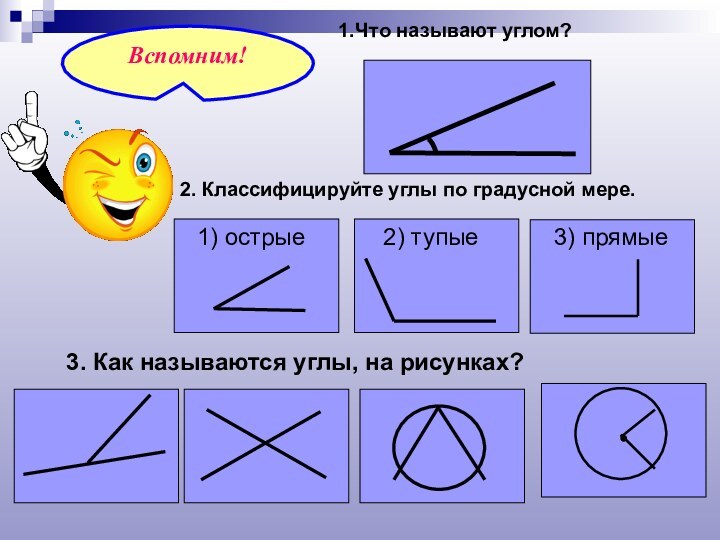
- 3. 1.Что называют углом?2. Классифицируйте углы по градусной мере.3. Как называются углы, на рисунках?
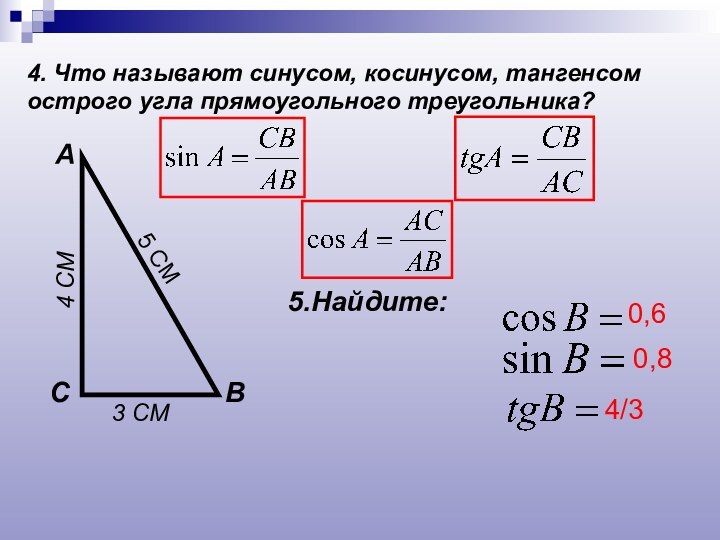
- 4. 4. Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника?АВС5.Найдите:3 СМ4 СМ5 СМ0,60,84/3
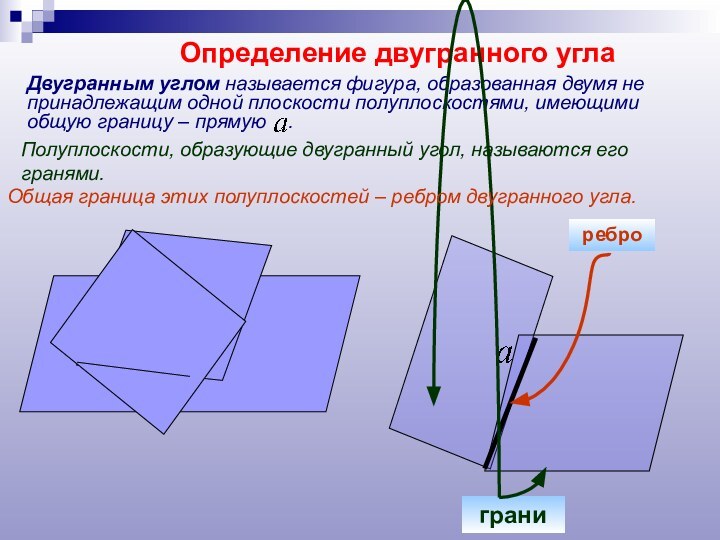
- 5. Определение двугранного углаДвугранным углом называется фигура, образованная
- 6. В обыденной жизни, форму двугранного угла имеют
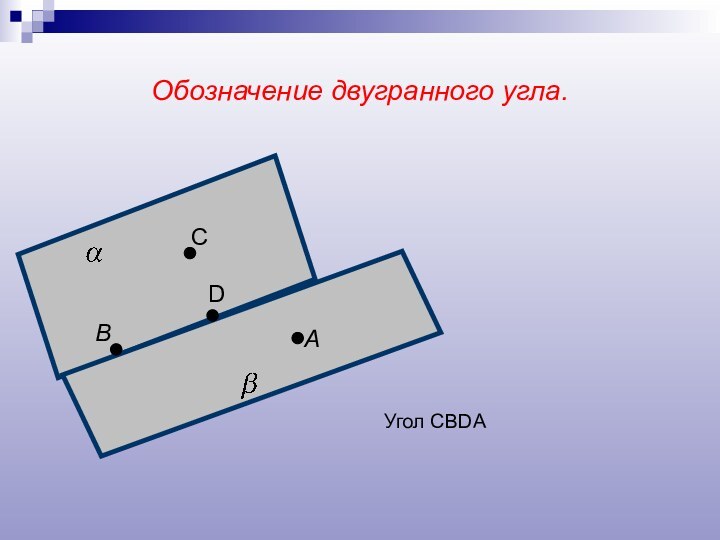
- 7. Обозначение двугранного угла.АВСDУгол CBDA
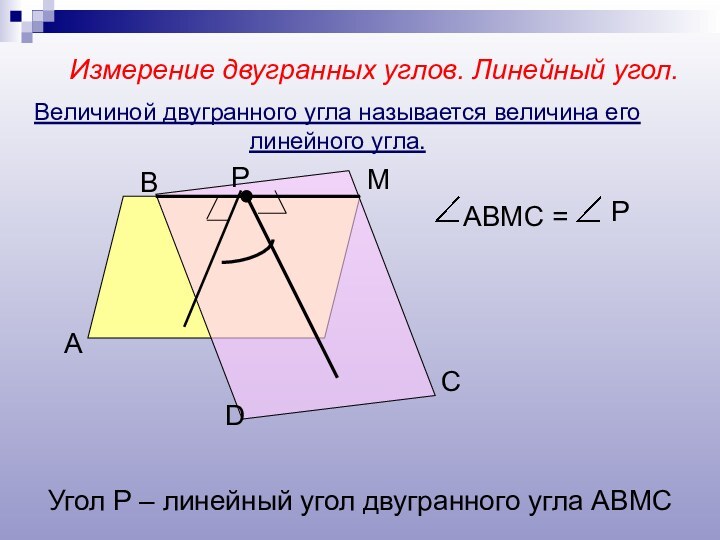
- 8. Измерение двугранных углов. Линейный угол.АВМDРСАВМС =РУгол Р
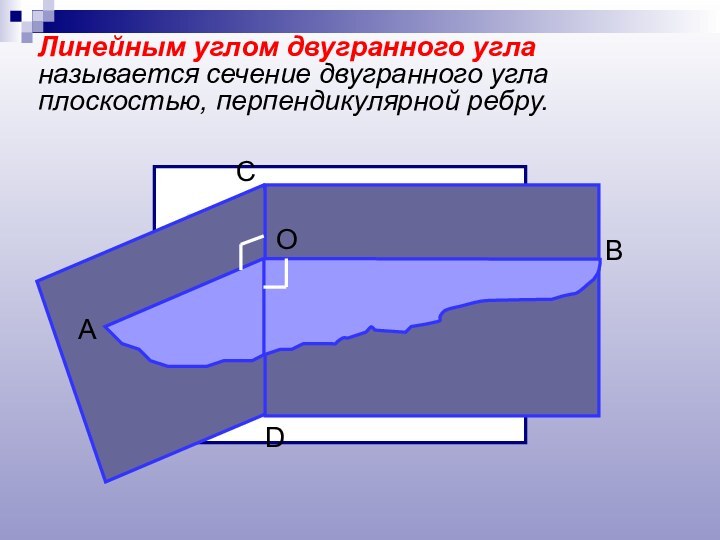
- 9. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 10. Способ нахождения (построения) линейного угла.1. Найти (
- 11. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.ABOA1O1B1
- 12. Двугранный угол является острым , прямым или
- 13. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.ββ1аαα1
- 14. АС АСРи АСВпрямая СВ перпендикулярна ребру
- 15. АСАСРи АСВВ грани АСВпрямая ВО перпендикулярна
- 16. Задача №3КМРТА) Двугранный угол РТМК: (1)
- 17. Задача №3КМРТВАСАВ параллельна РТ (по построению), а
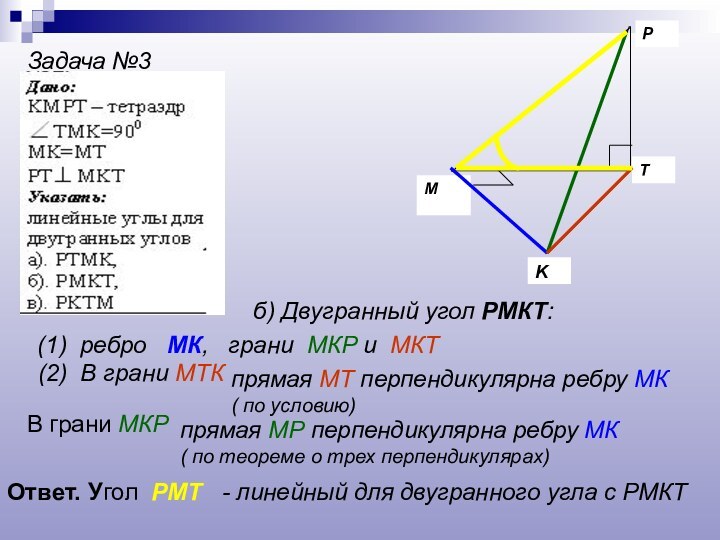
- 18. PKTMЗадача №3б) Двугранный угол РМКТ: (1) ребро
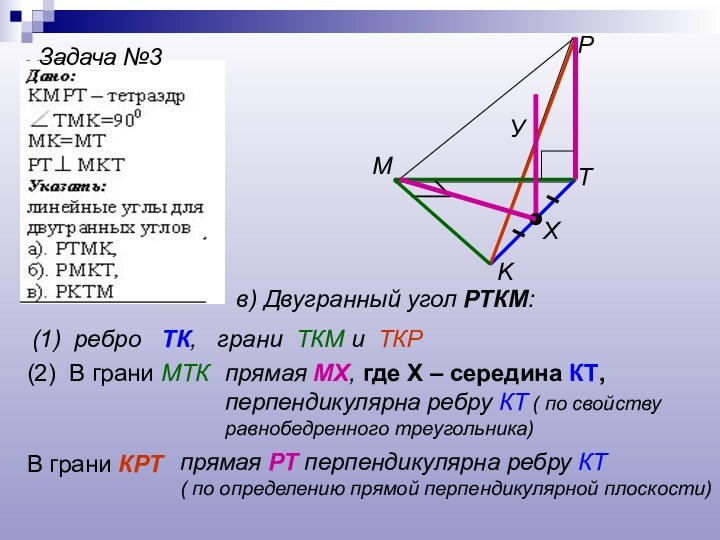
- 19. Задача №3TKPMв) Двугранный угол РТКМ: (1) ребро
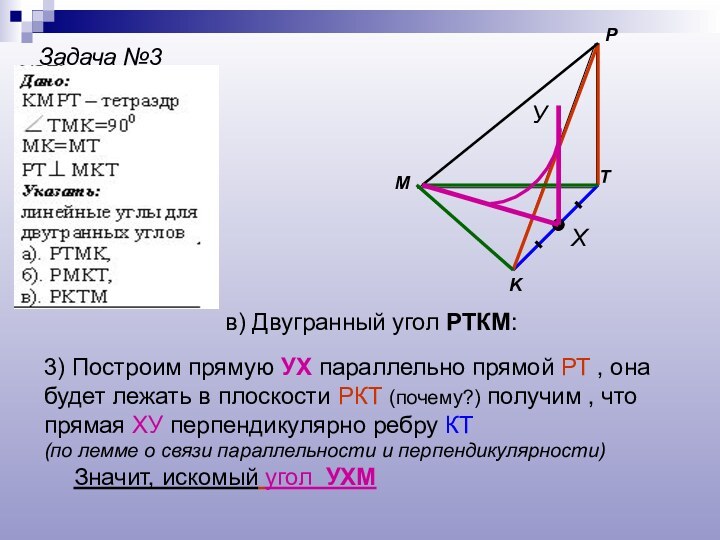
- 20. Задача №3MPKTХУв) Двугранный угол РТКМ:3) Построим прямую
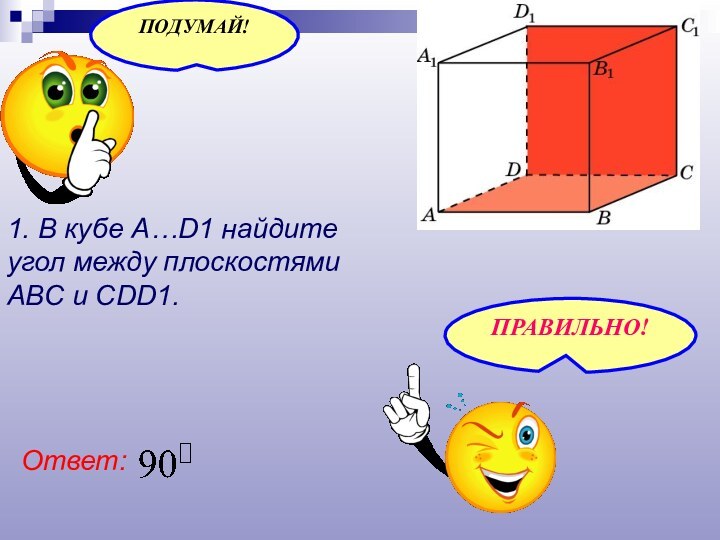
- 21. 1. В кубе A…D1 найдите угол между плоскостямиABC и CDD1.Ответ:
- 22. 2.В кубе A…D1 найдите угол между плоскостямиABC и CDA1.Ответ:
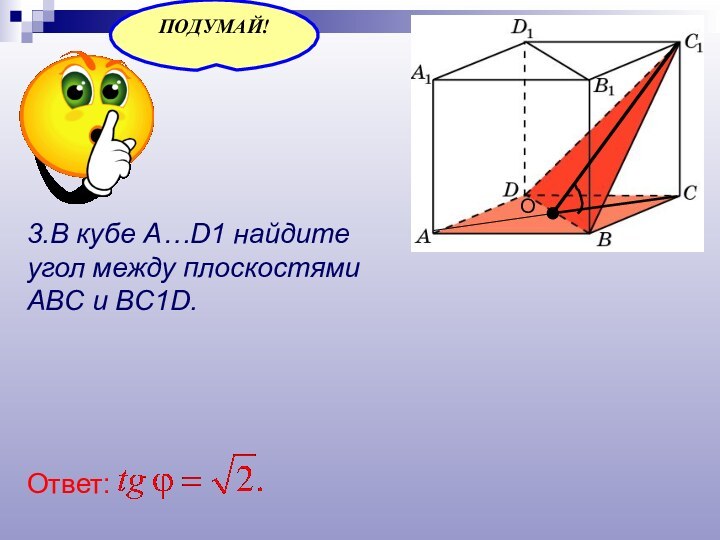
- 23. 3.В кубе A…D1 найдите угол между плоскостямиABC и BC1D.Ответ:О
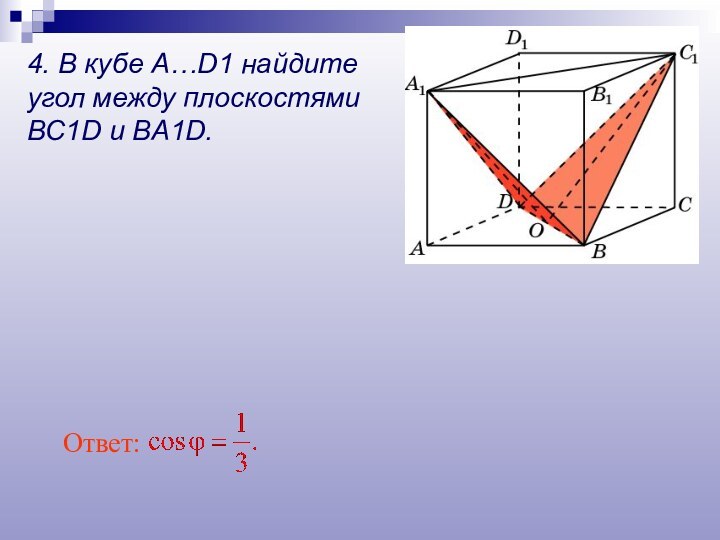
- 24. Ответ: 4. В кубе A…D1 найдите угол между плоскостямиBC1D и BA1D.
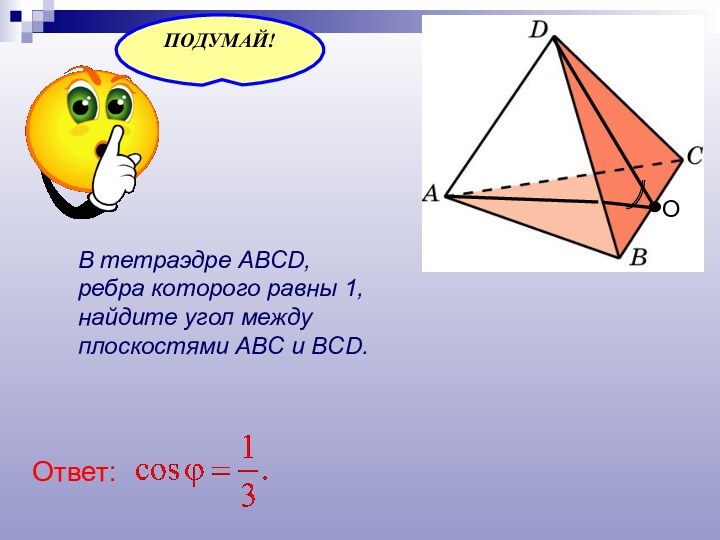
- 25. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD.ООтвет:
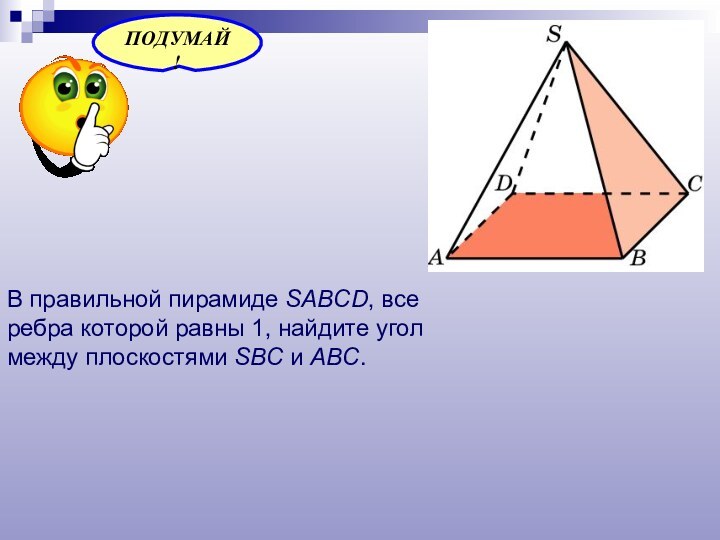
- 26. Скачать презентацию
- 27. Похожие презентации





Слайд 3
1.Что называют углом?
2. Классифицируйте углы по градусной мере.
3.
Как называются углы, на рисунках?
Слайд 4
4. Что называют синусом, косинусом, тангенсом острого угла
прямоугольного треугольника?
А
В
С
5.Найдите:
3 СМ
4 СМ
5 СМ
0,6
0,8
4/3
Слайд 5
Определение двугранного угла
Двугранным углом называется фигура, образованная двумя
не принадлежащим одной плоскости полуплоскостями, имеющими общую границу –
прямую .ребро
грани
Полуплоскости, образующие двугранный угол, называются его гранями.
Общая граница этих полуплоскостей – ребром двугранного угла.
Слайд 8
Измерение двугранных углов. Линейный угол.
А
В
М
D
Р
С
АВМС =
Р
Угол Р –
линейный угол двугранного угла АВМС
Величиной двугранного угла называется величина
его линейного угла.Слайд 9 Линейным углом двугранного угла называется сечение двугранного угла
плоскостью, перпендикулярной ребру.
Слайд 10
Способ нахождения (построения) линейного угла.
1. Найти ( увидеть)
ребро и грани двугранного угла
2. В гранях найти направления
( прямые) перпендикулярные ребру3. (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
При изображении сохраняется параллельность и отношение длин параллельных отрезков
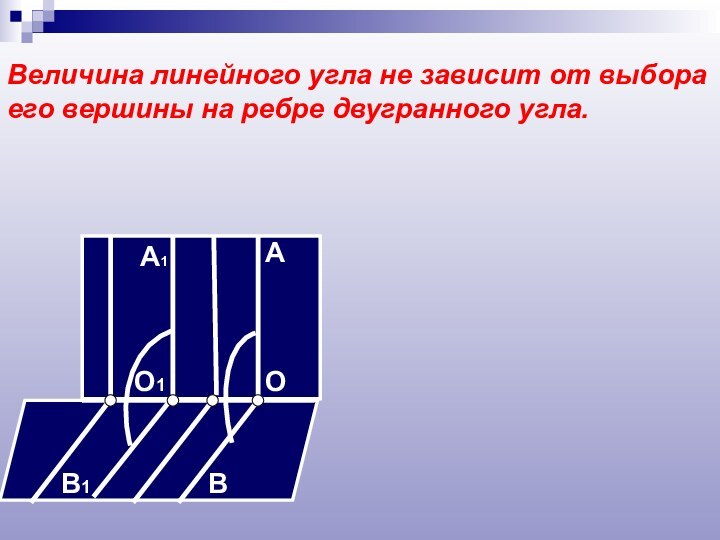
Слайд 11 Величина линейного угла не зависит от выбора его
вершины на ребре двугранного угла.
A
B
O
A1
O1
B1
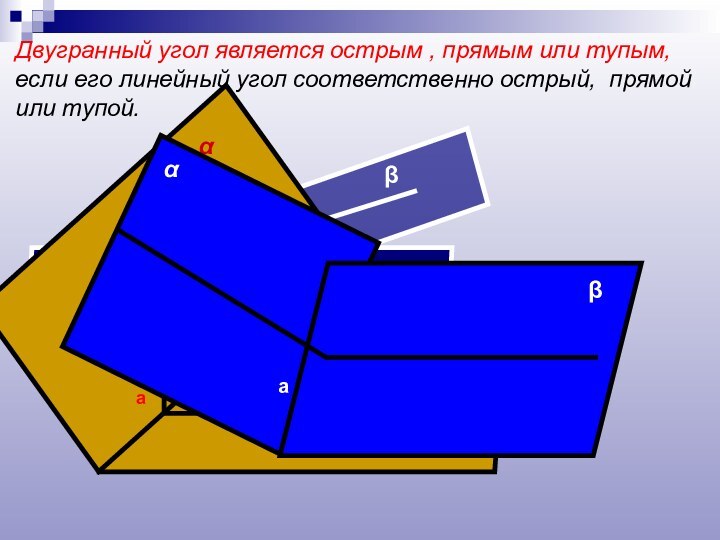
Слайд 12 Двугранный угол является острым , прямым или тупым,
если его линейный угол соответственно острый, прямой или тупой.
α
β
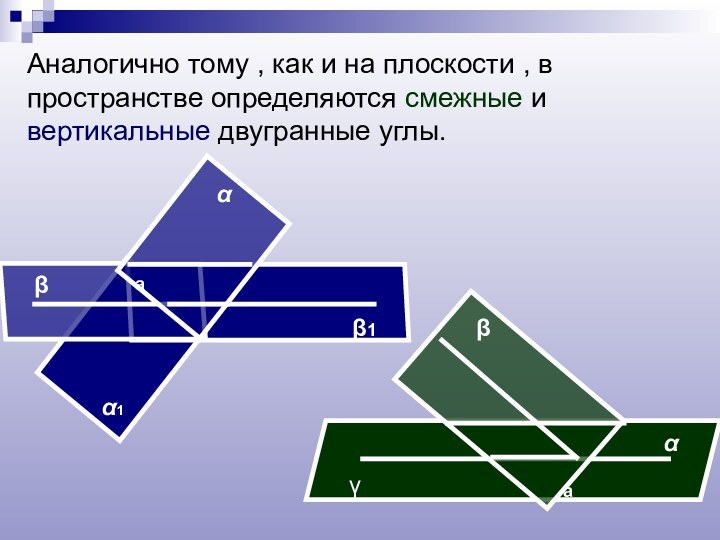
Слайд 13 Аналогично тому , как и на плоскости ,
в пространстве определяются смежные и вертикальные двугранные углы.
β
β1
а
α
α1
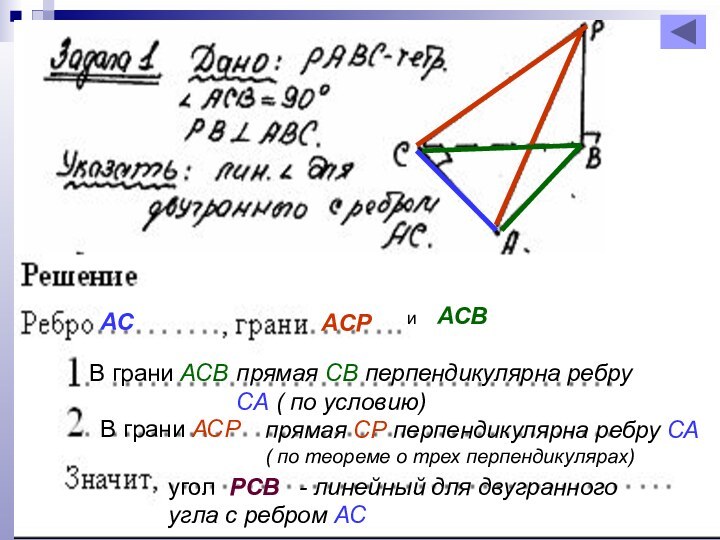
Слайд 14
АС
АСР
и АСВ
прямая СВ перпендикулярна ребру СА
( по условию)
В грани АСВ
В грани АСР
прямая СР перпендикулярна
ребру СА ( по теореме о трех перпендикулярах)
угол РСВ - линейный для двугранного угла с ребром АС
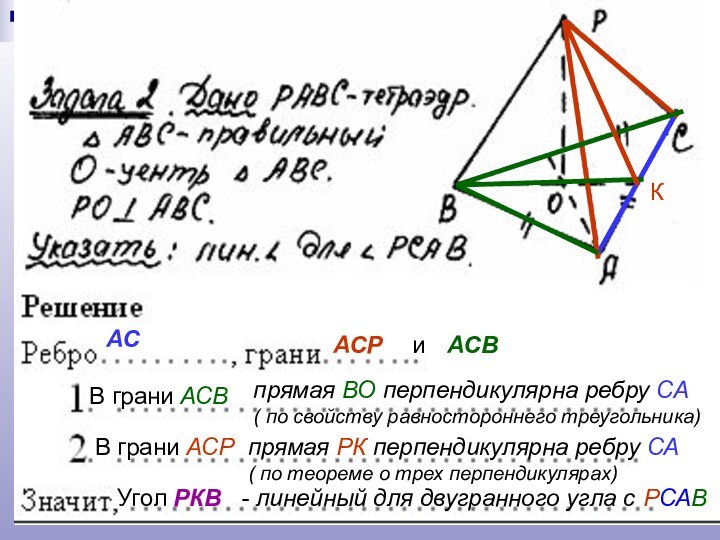
Слайд 15
АС
АСР
и АСВ
В грани АСВ
прямая ВО перпендикулярна ребру
СА
( по свойству равностороннего треугольника)
В грани АСР
прямая РК
перпендикулярна ребру СА ( по теореме о трех перпендикулярах)
Угол РКВ - линейный для двугранного угла с РСАВ
К
Слайд 16
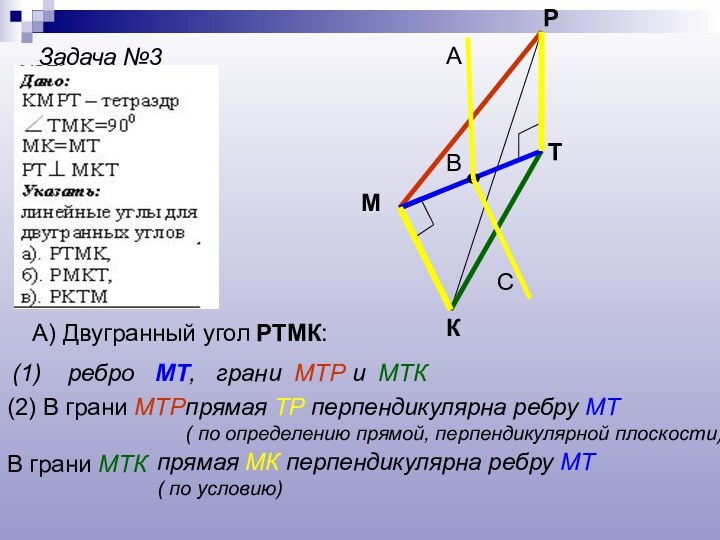
Задача №3
К
М
Р
Т
А) Двугранный угол РТМК:
(1) ребро
МТ, грани МТР и МТК
(2) В грани
МТРпрямая ТР перпендикулярна ребру МТ
( по определению прямой, перпендикулярной плоскости)
В грани МТК
прямая МК перпендикулярна ребру МТ
( по условию)
В
А
С
Слайд 17
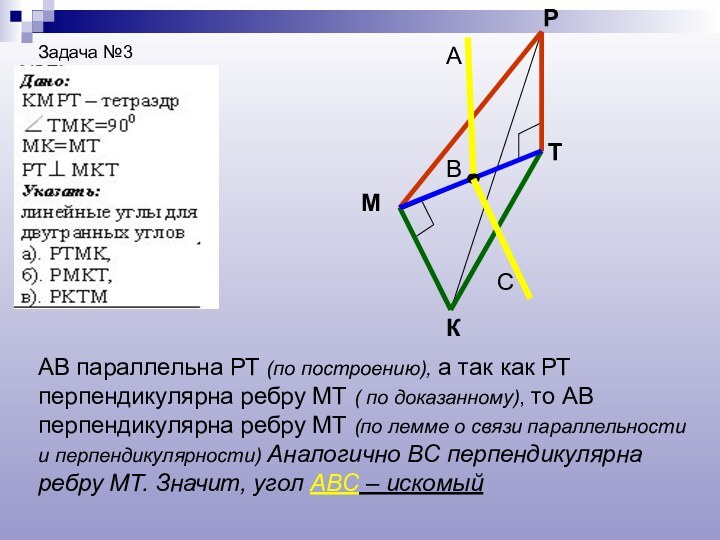
Задача №3
К
М
Р
Т
В
А
С
АВ параллельна РТ (по построению), а так
как РТ перпендикулярна ребру МТ ( по доказанному), то
АВ перпендикулярна ребру МТ (по лемме о связи параллельности и перпендикулярности) Аналогично ВС перпендикулярна ребру МТ. Значит, угол АВС – искомый
Слайд 18
P
K
T
M
Задача №3
б) Двугранный угол РМКТ:
(1) ребро
МК, грани МКР и МКТ
(2) В грани МТК
прямая
МТ перпендикулярна ребру МК ( по условию)В грани МКР
прямая МР перпендикулярна ребру МК
( по теореме о трех перпендикулярах)
Ответ. Угол РМТ - линейный для двугранного угла с РМКТ
Слайд 19
Задача №3
T
K
P
M
в) Двугранный угол РТКМ:
(1) ребро
ТК, грани ТКМ и ТКР
(2) В грани МТК
прямая
МХ, где Х – середина КТ, перпендикулярна ребру КТ ( по свойству равнобедренного треугольника)Х
В грани КРТ
прямая РТ перпендикулярна ребру КТ
( по определению прямой перпендикулярной плоскости)
У
Слайд 20
Задача №3
M
P
K
T
Х
У
в) Двугранный угол РТКМ:
3) Построим прямую УХ
параллельно прямой РТ , она будет лежать в плоскости
РКТ (почему?) получим , что прямая ХУ перпендикулярно ребру КТ(по лемме о связи параллельности и перпендикулярности)
Значит, искомый угол УХМ