Слайд 2
Актуальность темы
Проценты - это одна из сложнейших тем
математики, и очень многие учащиеся затрудняются или вообще не
умеют решать задачи на проценты. А понимание процентов и умение выполнять процентные вычисления и расчеты необходимы каждому человеку.
Изучение процентов, получение возможности решать разные задачи с их применением продиктовано самой жизнью, ведь с процентами мы сталкиваемся в повседневной жизни на каждом шагу. Познакомившись с процентами, я вдруг стал замечать, что они сопровождают нас повсюду: не только в школе (на уроках математики, географии, биологии, истории, и т.д.), но и в жизни: при оплате коммунальных услуг, на работе родителей при выплате заработной платы и налоговых, пенсионных удержаний из нее, в банке при оплате кредита или в интернете и т.д. На хорошем уровне ориентироваться в мире процентов не так уж и просто!
Слайд 3
В любом открытии есть 99 % труда и
потения
и только 1 % таланта и способностей.
Л. Магницкий
Слайд 4
Цели проекта
Показать, что тема «проценты» имеет широкое
практическое применение в разных сферах жизни человека, что изучение
процентов и умение производить процентные вычисления и расчеты для каждого человека просто необходимы.
Задачи проекта
Познакомиться с историей возникновения понятия «процент»
Рассмотреть решение трёх основных задач по теме «Проценты»
Выработать навыки решения основных задач на проценты.
Определить сферу практического применения процентов.
Слайд 5
План действий
Подобрать литературу, познакомиться с информацией в интернете
по истории возникновения процента.
Выучить определение процента и определить алгоритмы
решения основных задач на проценты.
Составить примеры основных задач на проценты, показать применение процентов в школьной жизни.
Составить задачи на проценты из современной жизни.
Собрать весь материал воедино и оформить продукт труда в виде презентации.
Слайд 6
Две версии возникновения знака %
Проценты - одно из
математических понятий, которые часто встречаются в повседневной жизни. Так,
мы часто читаем или слышим, что, например, в выборах приняли участие 56,5 % избирателей, рейтинг победителя хит-парада равен 80 %, промышленное производство сократилось на 10,3 %, уровень инфляции составляет 5 % в год, банк начисляет 12 % годовых, молоко содержит 3,2 % жира, материал содержит 60 % хлопка и т. д.
Слайд 7
Слово «процент» происходит от латинского слова pro centum,
что буквально означает «за сотню» или «со ста».
Знак «%»
происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буквы t превратилась в наклонную черту. Так произошел современный символ для обозначения процента.
Слайд 8
Существует и другая версия возникновения этого знака. Предполагается,
что этот знак произошел в результате нелепой опечатки, совершенной
наборщиком. В 1685 году в Париже была опубликована книга - руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Слайд 9
Процент. Основные понятия.
Процент — одна сотая доля.
Используется для обозначения доли чего-либо
по отношению к целому, например, 1 процент – 1 сотая часть числа 100: 1/100 = 1%
Проценты — удобная относительная мера, позволяющая производить действия с числами
в привычном для человека формате, вне зависимости от размера самих чисел. Это своего рода масштаб, к которому можно привести любое число.
Сотая часть числа – 1%
Десятая часть числа – 10%
Пятя часть числа – 20%
Четвёртая часть числа – 25%
Половина – 50%
Три четверти числа – 75%
Мы можем использовать проценты и для обозначения разных величин, например:
Один сантиметр - 1% от одного метра.
Одна копейка - 1% от одного рубля.
Один килограмм - 1% от одного центнера.
Слайд 11
Проценты в школьной жизни
Покажем, как можно использовать проценты
в школе.
Можно найти процентное количество мальчиков и девочек в
классе, их успеваемости; посчитать процент учащихся начального и среднего звена, старшеклассников в школе, процент классов, занимающихся в 1 и 2 смену, количество учителей, имеющих высшую и первую категорию, не имеющих ее. Аналогично можно посчитать проценты по разным темам в школе, по разным предметам школьной программы.
Слайд 12
Наш класс в процентах
Процент девочек и мальчиков в
классе.
Всего в 6 «б» классе 28 человек (100%), из
них 14 девочек (50%) и 14 мальчиков (50%).
Слайд 13
2) Успеваемость по математике
Успеваемость по математике – 100%
(28 человек)
Из них: учатся на «5» - 2 человека
(7%).
На «4» - 9 человек (32%).
На «3» - 17 человек (61%).
Слайд 14
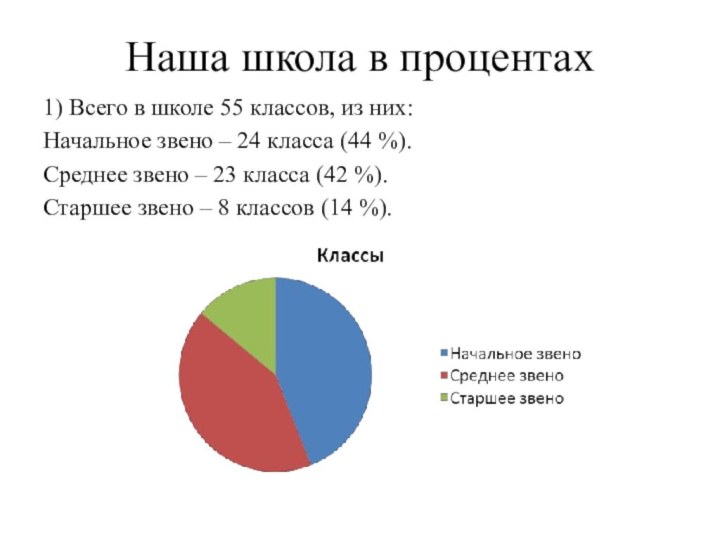
Наша школа в процентах
1) Всего в школе 55
классов, из них:
Начальное звено – 24 класса (44 %).
Среднее
звено – 23 класса (42 %).
Старшее звено – 8 классов (14 %).
Слайд 15
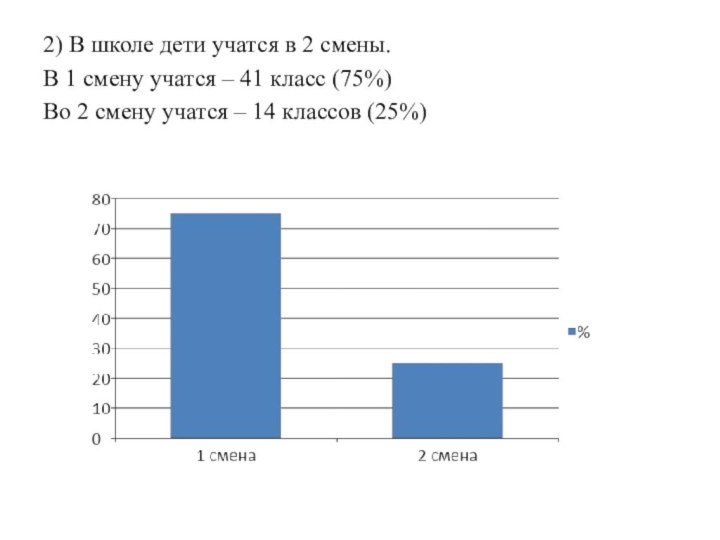
2) В школе дети учатся в 2 смены.
В
1 смену учатся – 41 класс (75%)
Во 2 смену
учатся – 14 классов (25%)
Слайд 16
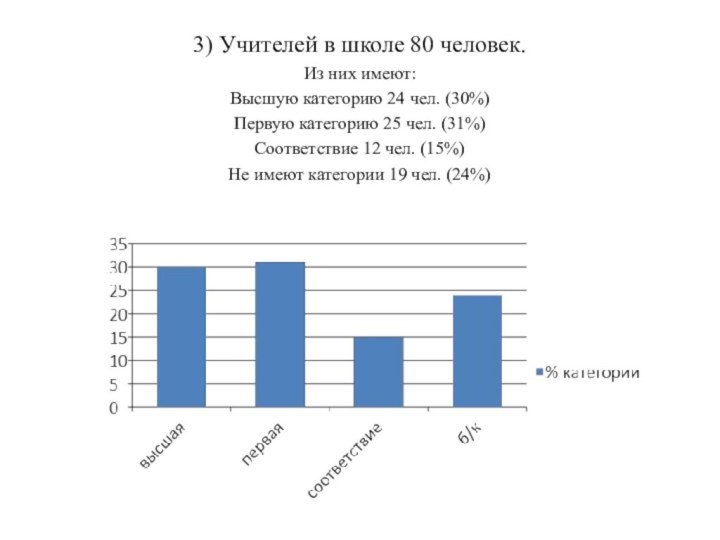
3) Учителей в школе 80 человек.
Из них имеют:
Высшую
категорию 24 чел. (30%)
Первую категорию 25 чел. (31%)
Соответствие 12
чел. (15%)
Не имеют категории 19 чел. (24%)
Слайд 17
Задачи на процентное вычисление в жизненных ситуациях.
Задача 1.
«Распродажа»
Стул стоил 1500 р. В декабре цена стула была
снижена на 20 %, а в январе еще на 10 %. Какой стала стоимость стула в январе?
Решение:
100%-это стоимость стула, 1500 руб.
1)1500:100=15(руб)-приходится на 1 %.
2)15·20=300(руб) сумма скидки 20%
3) 1500-300=1200 (руб) стал стоить стул после первого снижения цены
За 100% сейчас берём 1200 рублей
4) 1200:100=12(руб)-приходится на 1%
5)1200-12·10=1080(руб) стал стоить стул после второй скидки.
Ответ: 1080 рублей.
Слайд 18
Задача 2. «Бюджет. Зарплата»
При приеме на работу директор
предприятия предлагает зарплату 21500 руб. Какую сумму получит рабочий
после удержания налога? Налог составляет 13%.
Решение:
100%-это начисленная зарплата, 21500 рублей.
21500:100·13=2795(руб)-сумма налога на доход физических лиц
21500-2795=18705(руб)-сумма, который получит рабочий после удержания налога.
Ответ: 18 705 рублей
Слайд 19
Задача 3. «Банковский вклад»
Банк начисляет 12% годовых и
внесенная сумма равна 100 000 рублей. Какая сумма будет
на счете клиента банка через 3 года?
Решение:
100 000+100 000:100·12=112 000(руб)-через 1 год
112 000+112 000:100·12=125 440(руб)-через 2 года
125 440+125440:100·12=140 492,8(руб)-через 3 года
Ответ: на счёте клиента через 3 года будет 140 492,8руб.
Слайд 21
Вывод
Проценты дают возможность легко сравнивать между собой части
целого, упрощают расчёты и поэтому очень распространены.
В процессе выполнения
работы я узнал много нового, думаю, что проделал очень полезную работу для себя и это пригодится в учебе.
В последнее время экзамен по математике проводится в форме ЕГЭ, и в контрольно-измерительных материалах ЕГЭ присутствует задача на проценты. Поэтому нужно как можно лучше знать и уметь пользоваться этой темой.
В ходе реализации проекта на основании проделанной работы я показал, что процент - постоянный спутник нашей жизни. Таким образом, можно сказать, что мы живем в мире процентов.