Слайд 2
Литература
Экономико-математическое моделирование: Учебник для студентов вузов/ Под общ.
ред. И.Н. Дрогобыцкого.-М.:»Экзамен», 2004.
Лабскер Л.Г. Бабешко Л.О. Игровые методы
в управлении экономикой и бизнесом. М.:ДЕЛО, 2001.
Бережная Е.В., Бережной В.И. Математические методы в моделировании экономических систем. М.: ФиС, 2001.
Фомин Г.П. Математические методы и модели. М.: ФиС,2001.
Экономико-математическое моделирование
Слайд 3
Метод математического моделирования в экономике
Определение. ЭММ представляет собой
одну из фундаментальных математических дисциплин, стремящихся приоткрыть занавес над
устройством внутренних механизмов сложных экономических систем
Цель ЭММ – количественная оценка экономических процессов, протекающих в рамках исследуемой экономической системы
Экономическая система – любой хозяйствующий объект вне зависимости от формы собственности
Слайд 4
Известные ученые-экономисты
Леонид Витальевич Канторович родился 19 января 1912г.
в Санкт-Петербурге в семье врача. В 18 лет он
закончил математический факультет Ленинградского университета (1930) и уже через четыре года получил звание профессора. Л.В.Канторович является одним из основателей отечественных школ функционального анализа. вычислительной математики, языков программирования.
С 1938г. интересы Л.В.Канторовича были неразрывно связаны с экономическими исследованиями и решением народнохозяйственных проблем.
Крупнейшим его открытием является введение в математическую и экономическую науки понятия "линейное программирование" (1939). Линейное программирование является универсальной математической моделью оптимального функционирования экономических систем. Основная заслуга Л.В.Канторовича заключается в разработке единого подхода к широкому кругу экономических задач о наилучшем использовании ресурсов на базе линейного программирования.
Слайд 5
Известные ученые-экономисты
Василий Леонтьев
Родился в Санкт-Петербурге в 1906 г.
В 1925 г. окончил Ленинградский университет. В 1925-28 гг.
учился в Берлинском университете. В 1931 г. Леонтьев переезжает в США, где работает в течение 44 лет в Гарвардском университете
Особую известность Леонтьев получил как автор метода экономического анализа "затраты-выпуск" (Input-output). Этот метод использован Леонтьевым при построении моделей межотраслевых балансов экономики США
В круг его интересов входят математические методы и модели в экономике, международная торговля, анализ теорий Маркса и Кейнса, построение индексов, механизм спроса и предложения. экономические циклы и многое другое.
Слайд 6
Известные ученые-экономисты
Джон Мейнард Кейнс (1883 - 1946)
Дж. М.
Кейнс рассматривается большинством экономистов и политических деятелей как наиболее
значительный экономист-теоретик XX века.
Его научная разносторонность выявилась в том, что в молодости он достиг значительных успехов в математике и написал диссертацию по теории вероятности, а в более зрелом возрасте смог достичь выдающихся успехов и как экономист-теоретик,
Кейнс открыл целое направление исследований, в рамках которого сегодня работает чуть ли не половина всех экономистов мира. Речь идет о направлении, связанном с изучением функционирования экономики, взятой в целом, - о макроэкономике.
Слайд 7
Известные ученые-экономисты
Джон фон Не́йман (нем. John von Neumann,

или Янош Лайош Не́йман (28 декабря (28
декабря 1903 (28 декабря 1903 — 8 февраля (28 декабря 1903 — 8 февраля 1957 (28 декабря 1903 — 8 февраля 1957) — венгро (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана), применением теории операторов (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана), применением теории операторов, а также как участник Манхэттенского проекта (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана), применением теории операторов, а также как участник Манхэттенского проекта и как создатель теории игр (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана), применением теории операторов, а также как участник Манхэттенского проекта и как создатель теории игр и концепции (28 декабря 1903 — 8 февраля 1957) — венгро-немецкий математик , сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как праотец современной архитектуры компьютеров (так называемая архитектура фон Неймана), применением теории операторов, а также как участник Манхэттенского проекта и как создатель теории игр и концепции клеточных автоматов.
Слайд 8
Известные ученые-экономисты
Роберт Мертон Солоу; род. 23 августа; род.
23 августа 1924; род. 23 августа 1924, Нью-Йорк) — американский
экономист.
Лауреат Нобелевской премии 1987 г. «за фундаментальные исследования в области теории экономического роста».
Ветеран Второй мировой войны Ветеран Второй мировой войны. Профессор Массачусетского технологического института.
Президент Международной экономической ассоциацииПрезидент Международной экономической ассоциации (1999—2002). Президент Эконометрического обществаПрезидент Международной экономической ассоциации (1999—2002). Президент Эконометрического общества (1964). Президент Американской экономической ассоциации в 1979 г.
Награждён медалями Дж. Б. КларкаНаграждён медалями Дж. Б. Кларка (1961) и В. Леонтьева "За достижения в экономике" (2006).
Лауреат премий Джона КоммонсаЛауреат премий Джона Коммонса (1971), Ф. СейдманаЛауреат премий Джона Коммонса (1971), Ф. Сейдмана (1983) и А. Смита (1985).
Слайд 9
Известные ученые-экономисты
Гарри МАРКОВИЦ (род. в 1927 г.)
Особый интерес
с самого начала вызывала у него "экономика неопределенности", в
особенности, идеи Дж. фон Неймана, О. Моргенштерна, Дж. Маршака относительно функции полезности.
Для своей докторской диссертации М. избрал исследование возможности применения математических методов к рынку ценных бумаг. В процессе работы над темой у него сложилась в основном концепция портфельных инвестиций, за которую он впоследствии получит Нобелевскую премию
Главная заслуга Г.Марковца заключается в разработке точно сформулированной, пригодной для применения, теории для выбора портфельных инвестиций в условиях неопределенности, которая послужила основанием для последующих разработок в области экономики финансов.
Слайд 10
Известные ученые-экономисты
ПЕТТИ, УИЛЬЯМ (Petty, William) (1623–1687), английский экономист
и статистик. Родился 26 мая 1623 в семье небогатого
ремесленника-суконщика в Ромси (графство Хэмпшир).
Петти оставил заметный след в истории экономической науки, хотя единой точки зрения на его научный вклад до сих пор не существует. Основные труды Петти – Трактат о налогах и сборах (A Treatise of Taxes and Contributions, 1662); Слово мудрым (Verbum Sapienti, 1665); Политический обзор, или анатомия Ирландии (Political Survey or Anatomy of Ireland, 1672); Разное о деньгах (Quantulumcunque Concerning Money, 1682); и Эссе о политической арифметике (Essays in Political Arithmetick, 1683
Слайд 11
Известные ученые-экономисты
Кене Франсуа, (4 июня, (4 июня 1694,

(4 июня 1694 -16 декабря, (4 июня 1694 -16
декабря 1774, (4 июня 1694 -16 декабря 1774), французский, (4 июня 1694 -16 декабря 1774), французский экономист, (4 июня 1694 -16 декабря 1774), французский экономист, основоположник школы физиократов, (4 июня 1694 -16 декабря 1774), французский экономист, основоположник школы физиократов. К экономическим исследованиям Кёне приступил уже на склоне лет. Первые его статьи по этому предмету были напечатаны в «Энциклопедии» Дидро, (4 июня 1694 -16 декабря 1774), французский экономист, основоположник школы физиократов. К экономическим исследованиям Кёне приступил уже на склоне лет. Первые его статьи по этому предмету были напечатаны в «Энциклопедии» Дидро, в 1756, (4 июня 1694 -16 декабря 1774), французский экономист, основоположник школы физиократов. К экономическим исследованиям Кёне приступил уже на склоне лет. Первые его статьи по этому предмету были напечатаны в «Энциклопедии» Дидро, в 1756 г. В 1758 г. он напечатал «Экономическую таблицу»
Слайд 12
Основные понятия и определения
1. Элементы экономических задач:
Поиск ключевых
факторов, которые значимо влияют на результаты функционирования экономических систем.
Моделирование
потенциальных препятствий, которые возникают на пути развития экономической системы, и разработка способов их нейтрализации.
Составление количественных прогнозов развития экономических систем
Поиск альтернативных вариантов развития экономических систем.
Слайд 13
Основные понятия и определения.
2. Математическая модель и ее
свойства.
Определение. Математическая модель – это некоторый математический образ исследуемой
экономической системы, который адекватно отражает структуру переменных системы, их свойства и взаимосвязи.
Модель может быть представлена в виде набора графиков, таблиц или системы математических уравнений и неравенств, с помощью которых можно однозначно определить значения одних переменных по известным значениям других переменных.
Слайд 14
Основные понятия и определения
3. Основные свойства модели
Простота. Полнота.
Адекватность.
Простота. Проста в понимании. Простота математического аппарата. Не отягощена
лишними переменными, которые слабо влияют на развитие экономической системы (Все гениальное – просто)
Полнота. Включены все факторы, влияющие на достижение цели. Учтены все условия, которые ограничивают развитие системы. Имеется возможность получить ответ на все вопросы, поставленные в задаче.
Адекватность. Возможность достижения цели с приемлемой точностью.
Слайд 15
Основные понятия и определения
4. Основные свойства модели
Модель –
это компромисс между полнотой и простотой, точностью и размерностью,
эффективностью и затратами на ее реализацию.
Модель – объект заместитель объекта оригинала, который в определенных условиях может заменить оригинал.
Модель – результат идеализации и рафинирования реального экономического объекта.
Слайд 16
Основные понятия и определения
5. Переменные и параметры модели
Переменные
модели (факторы) – это переменные величины, которые характеризуют структуру
и состояние экономической системы
Экзогенные (независимые) переменные – это переменные, значения которых формируются вне модели
Эндогенные (зависимые) переменные – это переменные, значения которых формируются внутри модели, в зависимости от значений экзогенных переменных
Параметры модели – числовые константы, которые участвуют в модели с целью обеспечения ее адекватности
Слайд 17
Основные понятия и определения
6. Основная задача моделирования
Моделирование сводится
к тому, чтобы с помощью математических функций установить вид
связи между эндогенными и экзогенными переменными системы
Y = f(x1, x2,…,xk, a1,a2,…,an)
где: Y – эндогенная переменная;
xi – экзогенные переменные;
ai – параметры модели
Модель, в конечном счете, – некоторая функциональная связь между независимыми и зависимыми переменными
Слайд 18
Основные понятия и определения
7. Основные математические модели и
задачи
Задачи математического программирования
Модели конфликтных ситуаций в экономике
Модели сетевого планирования
и управления
Модели системы массового обслуживания
Модели сферы потребления
Модели сферы производства
Модели общего экономического равновесия
Общие модели развития экономики
Любая задача экономики сводится к задаче принятия решения или задаче управления
Слайд 19
Основные понятия и определения
Принятие решения является повседневной задачей
человека
Решения приходится принимать в различных ситуациях:
- как с наибольшей
пользой потратить имеющиеся средства
- как наиболее эффективно организовать производство того или иного продукта
- как рационально спланировать производственный цикл
-какую стратегию поведения выбрать, чтобы остаться «на плаву» в условиях конкуренции
Во всех случаях речь идет о выборе наилучшего (оптимального) решения.
В основе всех экономических проблем лежит задача оптимизации
Именно эти задачи занимают центральное место в экономико-математическом моделировании.
Слайд 20
Основные понятия и определения.
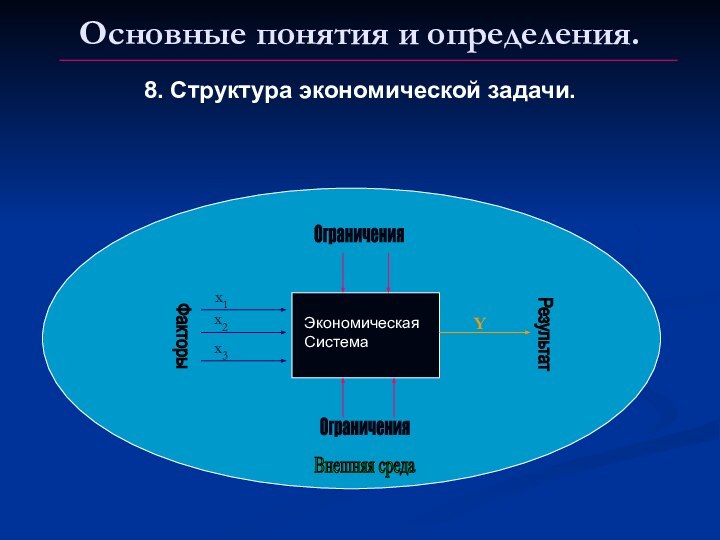
8. Структура экономической задачи.
Факторы
х1
х2
х3
Ограничения
Ограничения
Внешняя среда
Результат
Y
Экономическая
Система
Слайд 21
Основные понятия и определения
9. Этапы решения экономических задач
методами математического моделирования
Формализация экономической задачи
Сбор и первичная обработка информации
о изучаемой системе
Математическая обработка данных, построение модели
Решение экономической задачи с помощью полученной модели
Слайд 22
Основные понятия и определения
Формализация задачи
Всестороннее изучение структуры и
свойств экономической системы, выявление ограничений, факторов и переменных, на
основе имеющегося качественного анализа системы. Выбор класса функций и запись математической модели в общем виде.
Сбор и первичная обработка информации
Наблюдение за развитием экономической системы, регистрация значений всех переменных системы. Статистический анализ полученной информации на полноту и достоверность.