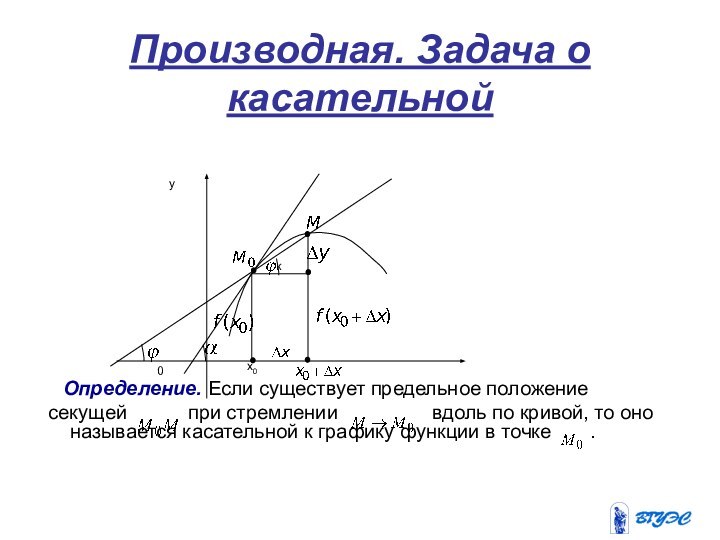
Дифференциал
4. Производные и дифференциалы высших порядков
5. Некоторые теоремы о
дифференцируемых функциях6.Применение производных к исследованию функций
7. Общая схема исследования функции и построение графика