Слайд 2
Цель : Понять, как построить циклоиды различные по
форме. Познакомиться с основными свойствами циклоиды (кривой второго порядка)
и проявлениями ее в жизни.
Задачи :
- изучить литературу по теме исследования;
- пополнить знания о разновидностях циклоиды и их свойствах;
- узнать о значении и применении циклоиды в жизни, окружающем мире, быту.
Слайд 3
Экспериментальное исследование
Определение: Циклоида – плоская кривая, которую описывает
фиксированная точка М, неподвижно связанная с окружностью, катящейся по
неподвижной прямой.
Если точка М расположена на окружности, то при вращении окружности по прямой получим линию – обычную циклоиду
Слайд 4
Если же точка N вне окружности, то удлиненную
циклоиду.
N
N
Слайд 5
Если же точка K внутри окружности, то укороченную
циклоиду.
K
K
Слайд 6
Определение: Кривая, описываемая точкой окружности, катящейся без скольжения
по другой окружности вне ее, называется эпициклоидой
Радиус движущейся
окружности в три раза меньше радиуса неподвижной.
Слайд 7
Если радиус неподвижной окружности равен радиусу подвижной, то
эпициклоиду называют кардиоидой .
Слайд 8
Определение: Плоская кривая, описываемая точкой окружности внутри неё,
называется гипоциклоидой
.
Радиус подвижной окружности в 4 раза меньше радиуса
неподвижной
Слайд 9
В зависимости от соотношения длин радиусов подвижной и
неподвижной окружностей, получаются различные формы гипоциклоид.
Если радиус неподвижной
окружности в 3 раза больше радиуса подвижной, то эта гипоциклоида называется астроидой
Слайд 10
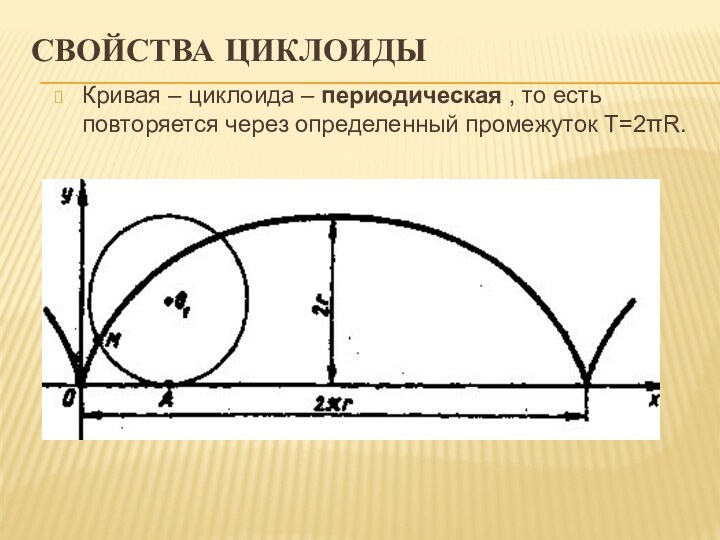
Свойства циклоиды
Кривая – циклоида – периодическая , то есть повторяется
через определенный промежуток Т=2πR.
Слайд 11
Изохронность циклоиды
свойство изохронности циклоиды (от греч. «изос» -равный,
«хронос» - время) навело Гюйгенса на мысль использовать ее
в часовом маятнике. Он предложил подвесить шарик на нити и ограничить свободу его перемещения доской, края которой имеют форму циклоиды.
Слайд 12
Брахистохронность циклоиды
(от греч. «брахистос»- кратчайщий и
«хронос»- время)
По циклоиде при отсутствии трения частица под
действием силы тяжести скатывается из одной заданной точки в другую за наименьшее время. Брахистохрона - это кривая наикратчайшего по времени спуска
Слайд 13
Из истории открытия циклоиды
Первым кто стал изучать циклоиду,
был Галилео Галилей (1564 -1642) – знаменитый итальянский астроном,
физик и просветитель. Он же и придумал название «циклоида». Это означает: «происходящий от круга или напоминающая о круге». Сам Галилей о циклоиде ничего не писал, но о его работах в этом направлении упоминают его ученики и последователи : Вивиани, Торричелли. Во Франции ее называли трохоидой или рулеттой . Позднее Паскаль удивлялся, что «эту кривую не рассмотрели древние», ибо «она так часто вычерчивается перед глазами каждого…Это ничто иное, как путь, описываемый в воздухе гвоздем колеса». Однако когда циклоида была открыта, она стала самой популярной кривой у математиков. В 1673 году Гюйгенс констатировал, что циклоида исследована точнее и основательнее других кривых.
Слайд 14
Парадоксы странные, но истинные
Слайд 16
Заключение
Математика – интересная и точная наука;
С помощью математических
выкладок и формул можно объяснить многие явления, происходящие в
природе;
Существует еще много интересных кривых, зная их свойства, можно сконструировать новые модели, применять на практике;
Геометрия – наука, занимающаяся изучением геометрических фигур и их свойств. Она таит в себе много интересного, не познанного еще нами.
Слайд 17
Изучение циклоид очень занимательно и полезно
для ума. Но если приложить немного усилий, терпения, усидчивости,
то обязательно получится красивая картина, а в её элементах без труда можно узнать нашу знакомую – циклоиду.
Слайд 18
Библиографический список
М.Д. Аксенова, Энциклопедия для детей. Т.11. Математика/–
М.: Аванта+, 1998.
И. Н. Бронштейн, К. Л. Семендяев Справочник
по математике для инженеров и учащихся ВТУЗов., М.: Гостехиздат.,1967.
Н.Я.Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.,Математика: Учеб.для 5кл. общеобразоват. учреждений / - М.: Мнемозина, 2012.
Н.Я.Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд.Математика: Учеб.для 6 кл. общеобразоват. учреждений / - М.: Мнемозина, 2012.
О.В. Мануров, Ю. К. Солнцев, Ю. И. Соркин, Н. Г. Федин; под ред. Л. В. Сабинина., Математика в понятиях, определениях и терминах. Ч. 2/. – М. Просвещение, 1982.
А.В.Погорелов.,Геометрия: учеб.для 7-9 кл. общеобразоват. учреждений / - М.: Просвещение, 2010.