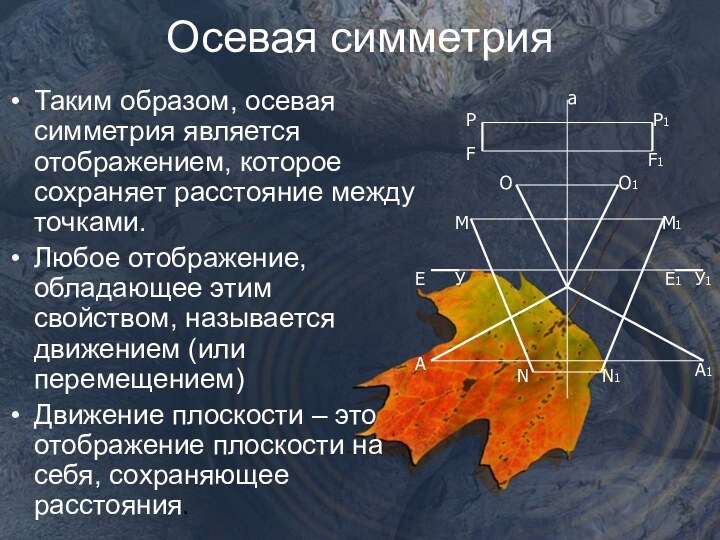
себя.
a
M1
M
P
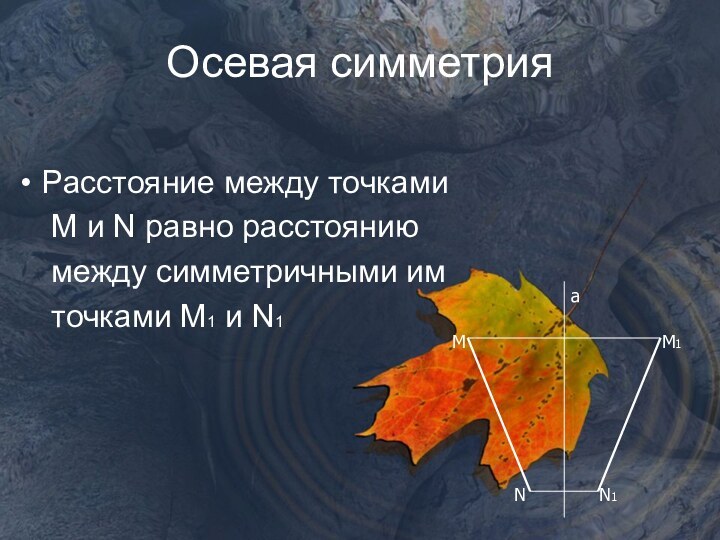
Пусть а – ось симметрии.
Возьмём М, не лежащую на
прямой а.Построим симметричную ей точку М1 относительно прямой а.
Для этого проведём перпендикуляр МР к прямой а.
Отложим на прямой МР отрезок РМ1, равный отрезку МР.
Точка М1 – искомая.