- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Формула корней квадратного уравнения
Содержание
- 2. Вы хотите научиться решать квадратные уравнения?ДАНЕТ
- 3. Вы хотите научиться решать квадратные уравнения?ДАНЕТ
- 4. Вы хотите научиться решать квадратные уравнения?ДАНЕТ
- 5. СодержаниеОпределение квадратного уравненияДискриминант квадратного уравненияФормула корней квадратного уравненияЗадачиПолезный материалТестСамостоятельная работа
- 6. Определение квадратного уравнения.Опр. 1. Квадратным уравнением называется
- 7. Дискриминант квадратного уравненияОпр. 2. Дискриминантом квадратного уравнения
- 8. Если D 0В этом случае уравнение
- 9. Если D = 0В этом случае уравнение
- 10. Если D 0Уравнение ах2 + bх + с = 0 не имеет действительных корней.
- 11. Формула корней квадратного уравненияОбобщив рассмотренные случаи получаем
- 12. ЗадачиРешить уравнение 2x2- 5x + 2 = 0.Решить уравнение 2x2- 3x +
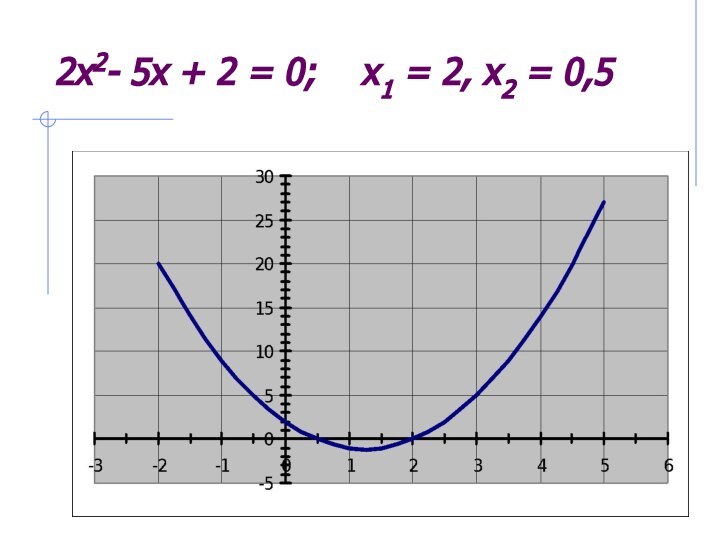
- 13. Решить уравнение 2x2- 5x + 2 = 0Здесь a = 2, b = -5, c = 2. Имеем
- 14. 2x2- 5x + 2 = 0; x1 = 2, x2 = 0,5
- 15. Решить уравнение 2x2- 3x + 5 =
- 16. Решить уравнение x2- 2x + 1 =
- 17. Полезный материал Определение квадратного уравненияОпределение приведенного квадратного уравненияОпределение дискриминантаФормула корней квадратного уравненияКоэффициенты квадратного уравнения
- 18. Определение приведенного квадратного уравненияОпр. 3. Приведенным квадратным
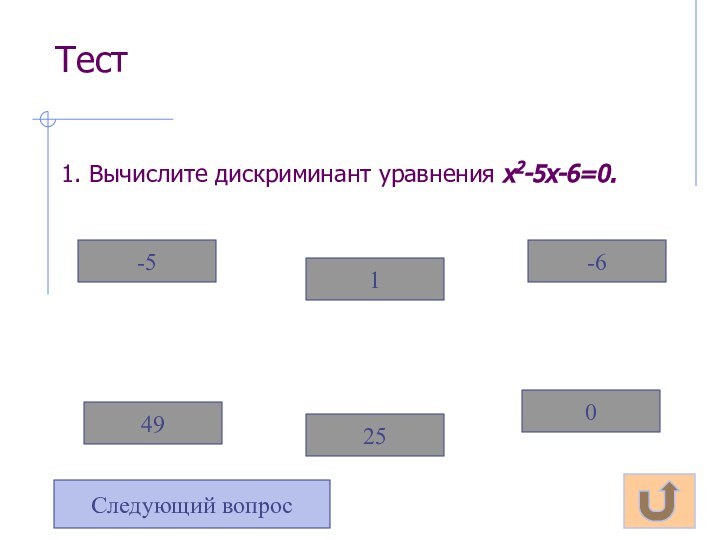
- 19. Тест1. Вычислите дискриминант уравнения х2-5х-6=0.0-6125-549Следующий вопрос
- 20. 2. Сколько корней имеет уравнение, если D < 0?Три корняОдин кореньДва корняКорней не имеетСледующий вопрос
- 21. 3. Выберите корни уравнения 2у2-9у+10=0.у1=-2; у2=-2,5Корней не имеету1=2; у2=-2,5у1=2; у2=2,5
- 22. Самостоятельная работа Вариант 1.№1. Решите уравнения:а) х2+7х-44=0;б)
- 24. Молодец !
- 25. Скачать презентацию
- 26. Похожие презентации
Вы хотите научиться решать квадратные уравнения?ДАНЕТ



















Слайд 5
Содержание
Определение квадратного уравнения
Дискриминант квадратного уравнения
Формула корней квадратного уравнения
Задачи
Полезный
материал
Слайд 6
Определение квадратного уравнения.
Опр. 1. Квадратным уравнением называется уравнение
вида ах2 + bх + с = 0, где
х –переменная, а, b и с - некоторые числа, причем а 0.Числа а, b и с - коэффициенты квадратного уравнения. Число а называют первым коэффициентом, b – вторым коэффициентом и с – свободным членом.
Слайд 7
Дискриминант квадратного уравнения
Опр. 2. Дискриминантом квадратного уравнения ах2
+ bх + с = 0 называется выражение b2
– 4ac. Его обозначают буквой D, т.е. D= b2 – 4ac.Возможны три случая:
D 0
D 0
D 0
Слайд 11
Формула корней квадратного уравнения
Обобщив рассмотренные случаи получаем
формулу
корней квадратного уравнения
ах2 + bх + с = 0.
К
тесту
Слайд 12
Задачи
Решить уравнение 2x2- 5x + 2 = 0.
Решить уравнение 2x2- 3x + 5
= 0.
Решить уравнение x2- 2x + 1 = 0.
Слайд 13
Решить уравнение 2x2- 5x + 2 = 0
Здесь a = 2, b = -5, c = 2.
Имеем D = b2- 4ac = (-5)2- 422 = 9.
Так как D > 0, то уравнение имеет два корня.
Найдем их
по формулето есть x1 = 2 и x2 = 0,5 - корни заданного уравнения.
К задачам
Слайд 15
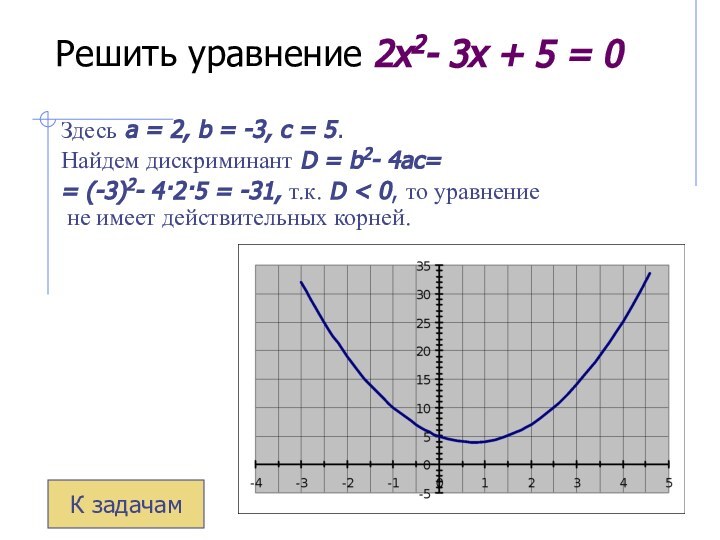
Решить уравнение 2x2- 3x + 5 = 0
Здесь
a = 2, b = -3, c = 5.
Найдем дискриминант D = b2- 4ac=
= (-3)2- 4·2·5 = -31,
т.к. D < 0, то уравнение
не имеет действительных корней. К задачам
Слайд 16
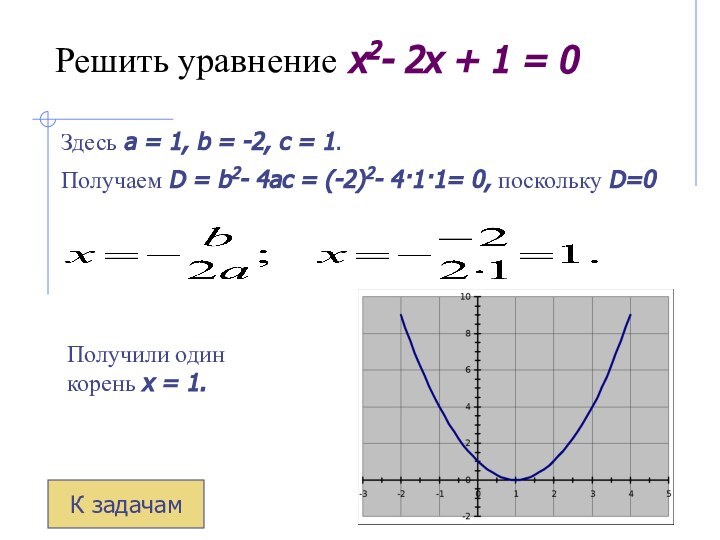
Решить уравнение x2- 2x + 1 = 0
Здесь
a = 1, b = -2, c = 1.
Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0
Получили один
корень х = 1.К задачам
Слайд 17
Полезный материал
Определение квадратного уравнения
Определение приведенного квадратного уравнения
Определение
дискриминанта
Формула корней квадратного уравнения
Коэффициенты квадратного уравнения
Слайд 18
Определение приведенного квадратного уравнения
Опр. 3. Приведенным квадратным уравнением
называется квадратное уравнение, первый коэффициент которого равен 1.
х2 +
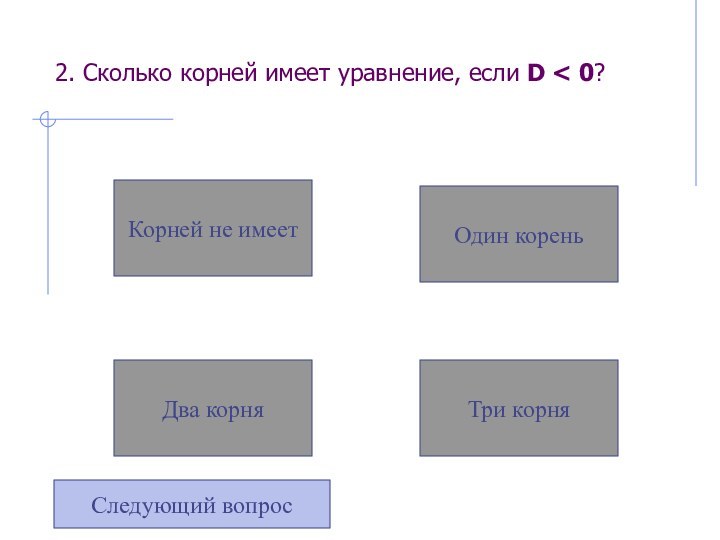
bх + с = 0Слайд 20 2. Сколько корней имеет уравнение, если D
0?
Три корня
Один корень
Два корня
Корней не имеет
Следующий вопрос
Слайд 21
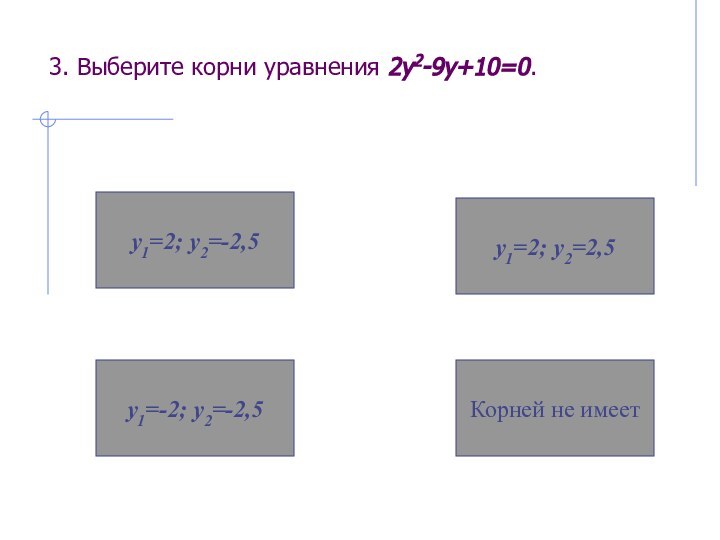
3. Выберите корни уравнения 2у2-9у+10=0.
у1=-2; у2=-2,5
Корней не имеет
у1=2;
у2=-2,5
у1=2; у2=2,5
Слайд 22
Самостоятельная работа
Вариант 1.
№1. Решите уравнения:
а) х2+7х-44=0;
б) 9у2+6у+1=0;
в)
–2t2+8t+2=0;
г) а+3а2= -11.
№2. При каких
значениях х равны значения многочленов:
(2-х)(2х+1)
и (х-2)(х+2)?Вариант 2.
№1. Решите уравнения:
а) х2-10х-39=0;
б) 4у2-4у+1=0;
в) –3t2-12t+6=0;
г) 4а2+5= а.
№2. При каких
значениях х равны значения многочленов:
(1-3х)(х+1) и (х-1)(х+1)?





























