Курс математического анализа, т. 1, 2
Г. Н.
Берман. Сборник задач по курсу математического анализа. Н. С. Пискунов. Дифференциальное и интегральное исчисления, т. 1, 2.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









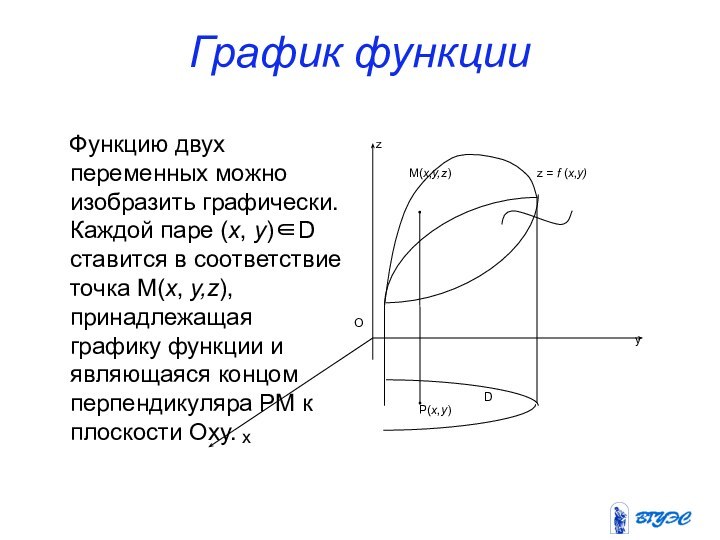
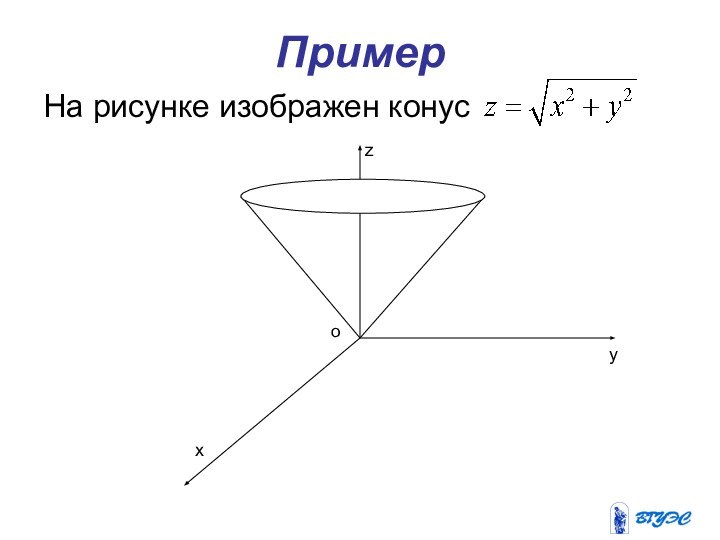

















х
.
о
х
у