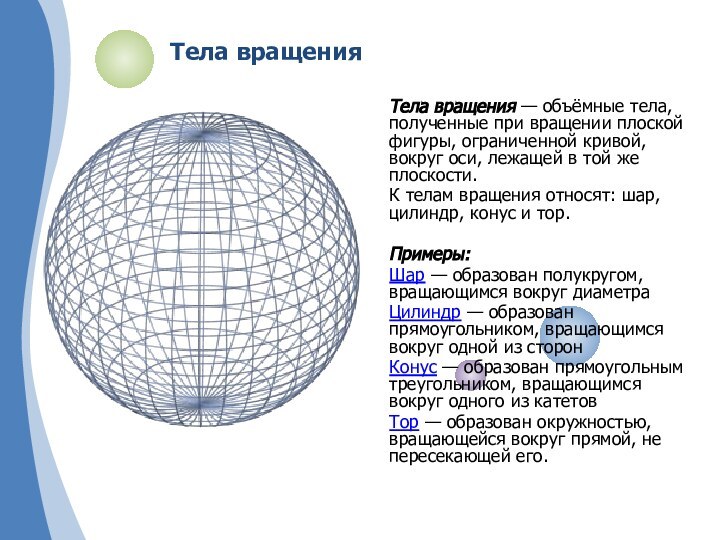
плоской фигуры, ограниченной кривой, вокруг оси, лежащей в той
же плоскости.К телам вращения относят: шар, цилиндр, конус и тор.
Примеры:
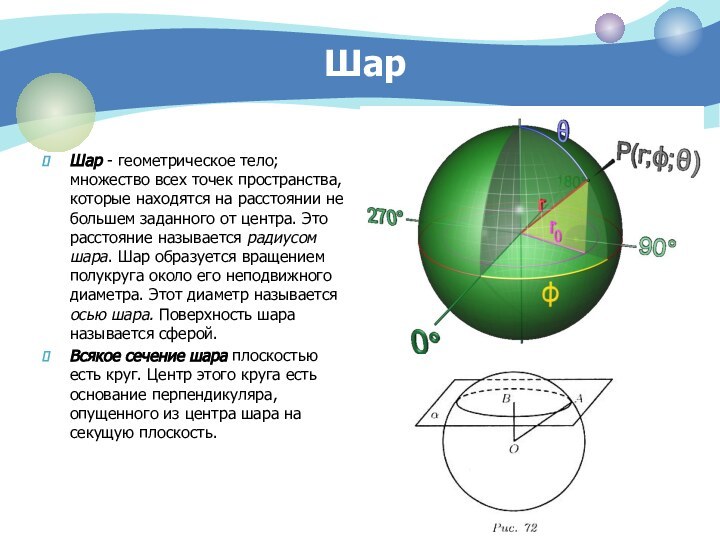
Шар — образован полукругом, вращающимся вокруг диаметра
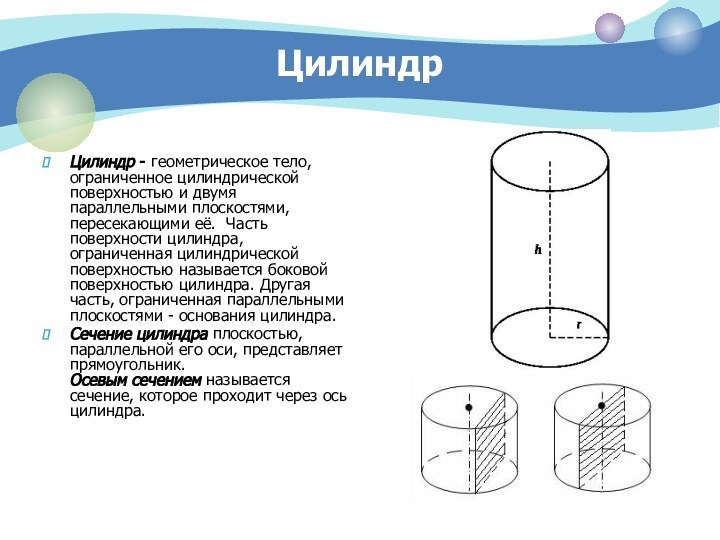
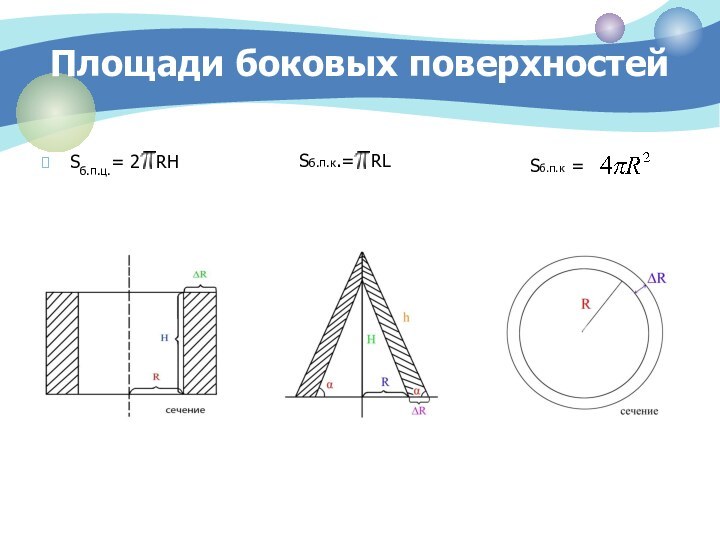
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон
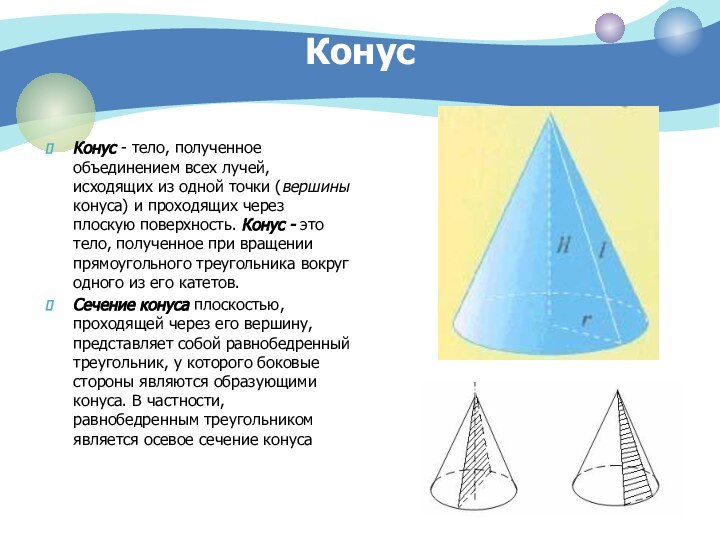
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его.