- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия правильные многоугольники
Содержание
- 2. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ-ОДНА ИЗ ЛЮБИМЫХ ФОРМ В ПРИРОДЕ
- 3. ПОНЯТИЕ ПРАВИЛЬНОГО МНОГОУГОЛЬНИКАВыпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны
- 4. Каково бы ни было число n,
- 5. Основное СВОЙСТВо ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВПравильный многоугольник является вписанным
- 6. О ЦЕНТРЕ ПРАВИЛЬНОГО МНОГОУГОЛЬНИКАВ каждом правильном многоугольнике
- 7. Около любого правильного многоугольника можно описать окружность,
- 8. В любой правильный многоугольник можно вписать окружность,
- 9. ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ- ЭТО ДЕЛЕНИЕ ОКРУЖНОСТИ НА
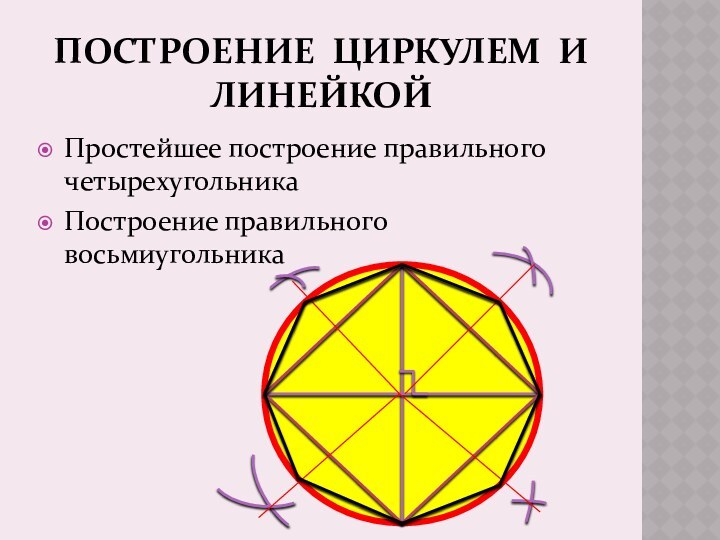
- 10. ПОСТРОЕНИЕ ЦИРКУЛЕМ И ЛИНЕЙКОЙПростейшее построение правильного четырехугольникаПостроение правильного восьмиугольника
- 11. Если построен какой-нибудь правильный n-угольник, то с
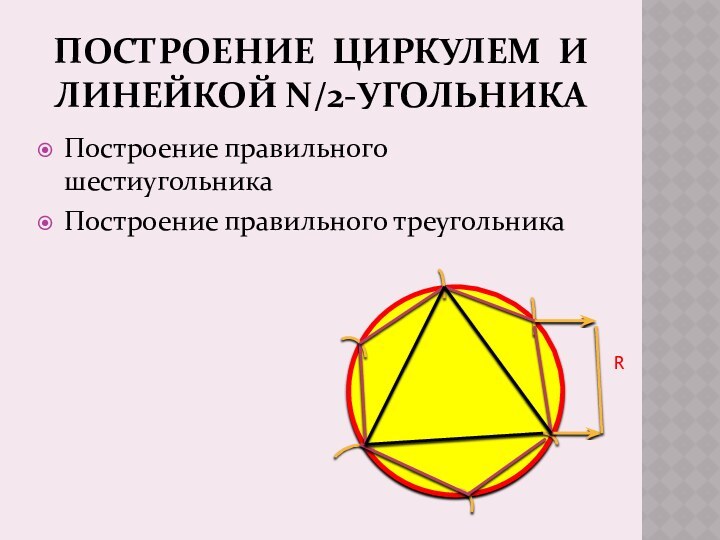
- 12. ПОСТРОЕНИЕ ЦИРКУЛЕМ И ЛИНЕЙКОЙ N/2-УГОЛЬНИКАПостроение правильного шестиугольникаПостроение правильного треугольника R
- 13. обоснуйте шаги построения правильного 6-угольника
- 14. ОБОСНОВАНИе построения правильного 6-угольника
- 15. Правильные многоугольники – воплощение красоты и изящества. Они заслуживают пристального внимания и изучения.
- 16. Скачать презентацию
- 17. Похожие презентации
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ-ОДНА ИЗ ЛЮБИМЫХ ФОРМ В ПРИРОДЕ
Слайд 3
ПОНЯТИЕ ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА
Выпуклый многоугольник называется правильным, если у
него все углы равны и все стороны равны
Слайд 4 Каково бы ни было число n, больше
двух, существует правильный n-угольник.
Возьмем какую-нибудь окружность с центром
в точке О и разделим её на n равных дуг. Для этого проведем радиусы ОА1, ОА2,…, ОАn этой окружности так, чтобы угол А1ОА2= угол А2ОА3 =…= угол Аn-1ОАn= угол АnОА1= 360°/n (на рисунке n=8). Если теперь провести отрезки А1А2, А2А3,…, Аn-1Аn, АnА1, то получим n- угольник А1А2…Аn. Треугольники А1ОА2, А2ОА3,…, АnОА1 равны друг другу (ДОКАЖИТЕ!),
поэтому А1А2= А2А3=…= Аn-1Аn= АnА1. Отсюда следует, что А1А2…Аn- правильный n- угольник.
Слайд 5
Основное СВОЙСТВо ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Правильный многоугольник является вписанным в
окружность и описанным около окружности, причем центры этих окружностей
совпадают.
Слайд 6
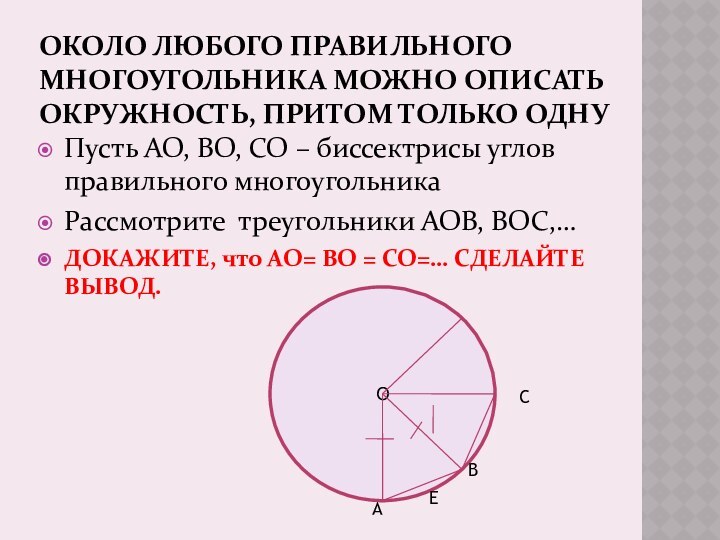
О ЦЕНТРЕ ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА
В каждом правильном многоугольнике есть
точка, равноудаленная от всех его вершин и всех его
сторон- центр.ДОКАЖИТЕ!
О
А
В
С
Е
К
Слайд 7 Около любого правильного многоугольника можно описать окружность, притом
только одну
Пусть АО, ВО, СО – биссектрисы углов правильного
многоугольникаРассмотрите треугольники АОВ, ВОС,…
ДОКАЖИТЕ, что АО= ВО = СО=… СДЕЛАЙТЕ ВЫВОД.
О
А
В
С
Е
Слайд 8 В любой правильный многоугольник можно вписать окружность, притом
только одну
Пусть АВС…-правильный многоугольник, О- центр описанной окружности.
Высоты треугольников
АОВ, ВОС,… равны между собой. ДОКАЖИТЕ!Сделайте вывод.
О
А
В
С
Е
Слайд 9 ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ- ЭТО ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ
ЧАСТИ
Классическая геометрия признает только построения при
помощи циркуля и линейки
Слайд 10
ПОСТРОЕНИЕ ЦИРКУЛЕМ И ЛИНЕЙКОЙ
Простейшее построение правильного четырехугольника
Построение правильного
восьмиугольника
Слайд 11 Если построен какой-нибудь правильный n-угольник, то с помощью
циркуля и линейки можно построить правильный 2n-угольник, 4n-УГОЛЬНИК и,
вообще, (2^k*n)-угольник, где k - любое натуральное число.
Слайд 12
ПОСТРОЕНИЕ ЦИРКУЛЕМ И ЛИНЕЙКОЙ N/2-УГОЛЬНИКА
Построение правильного шестиугольника
Построение правильного
треугольника
R
Слайд 15 Правильные многоугольники – воплощение красоты и изящества.
