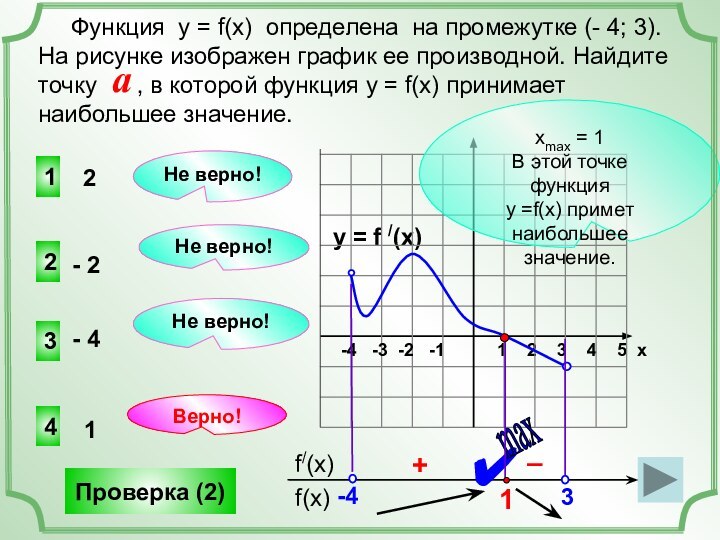
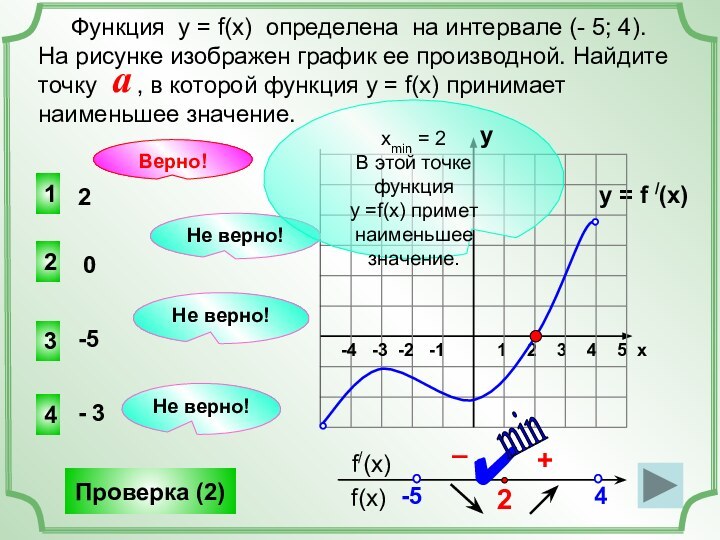
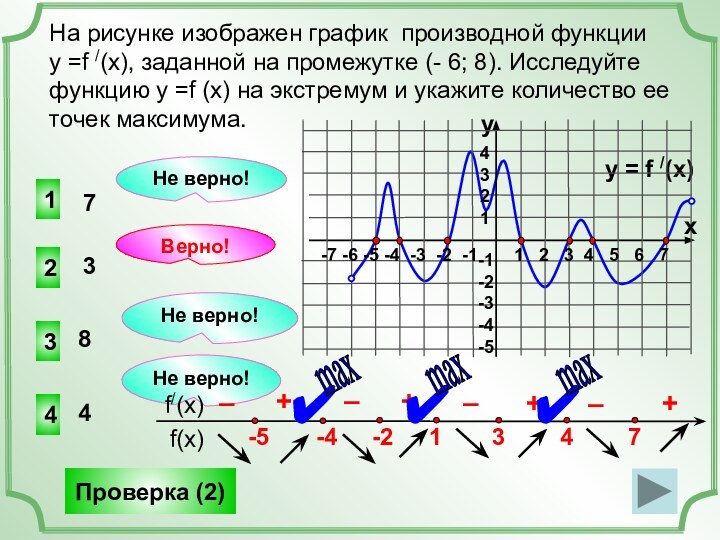
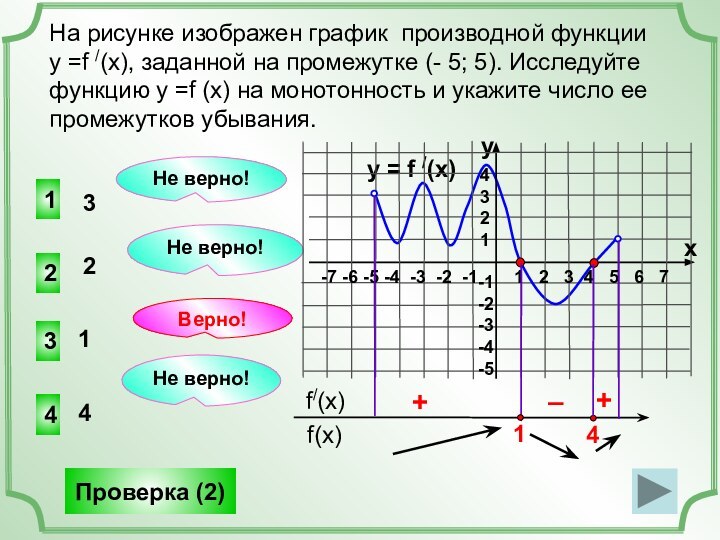
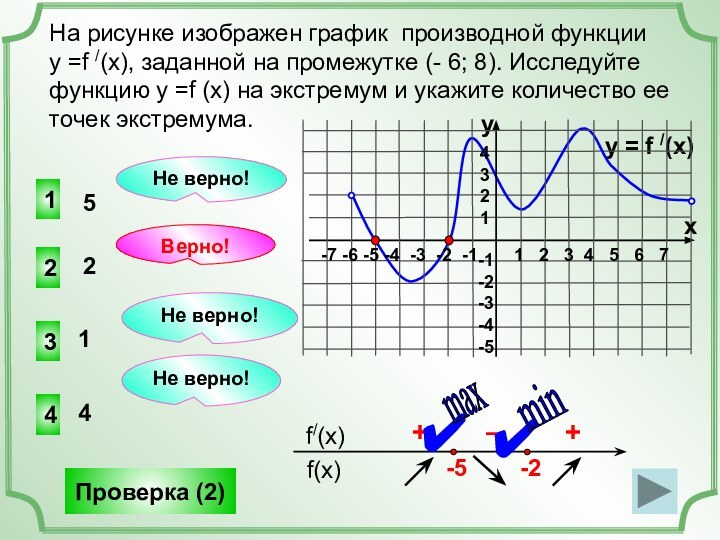
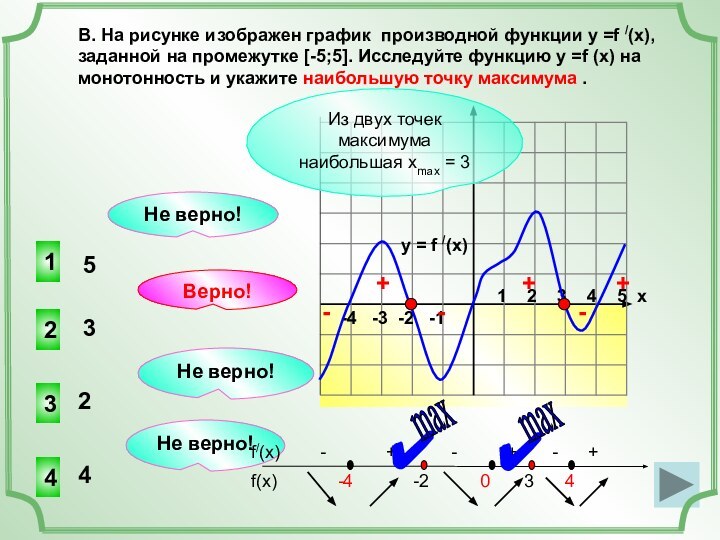
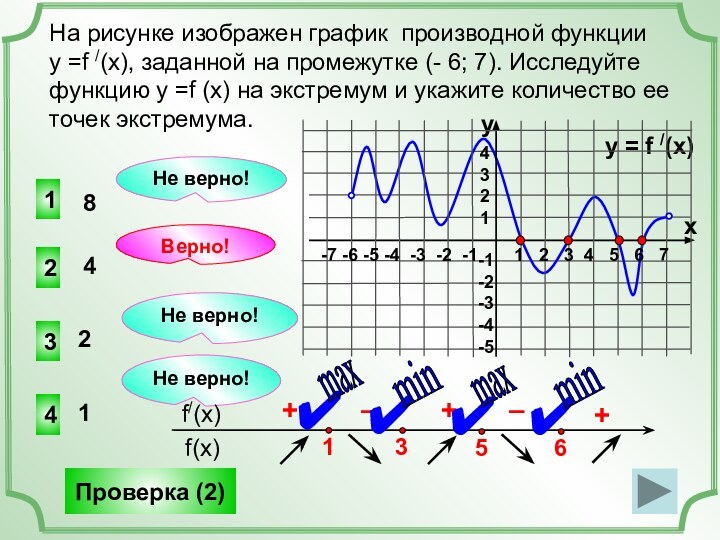
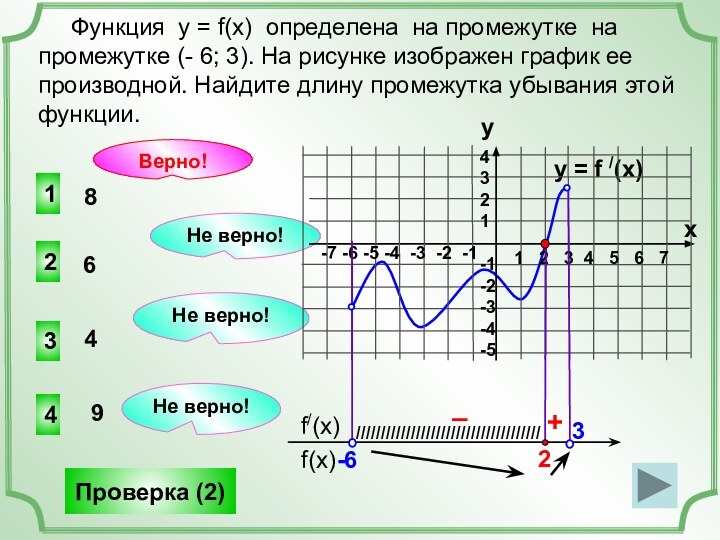
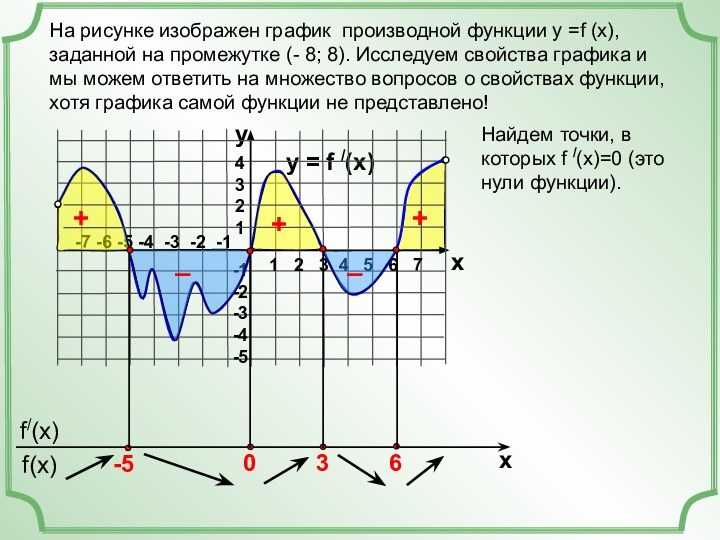
(x), заданной на промежутке (- 8; 8). Исследуем свойства
графика и мы можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено!y = f /(x)
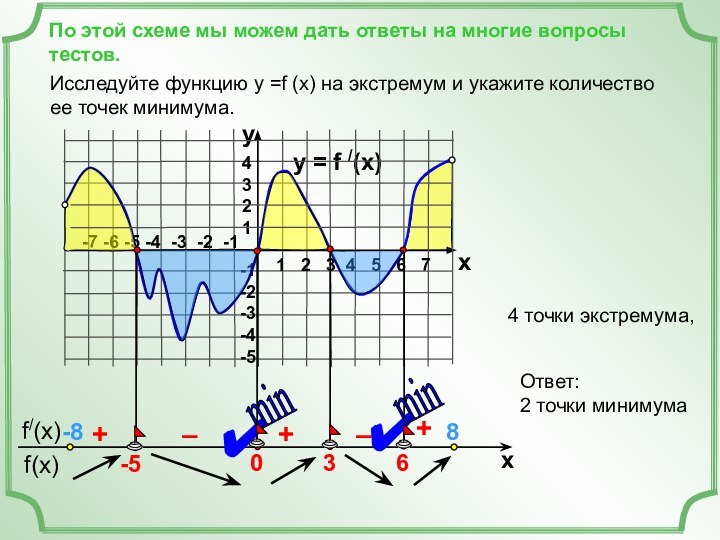
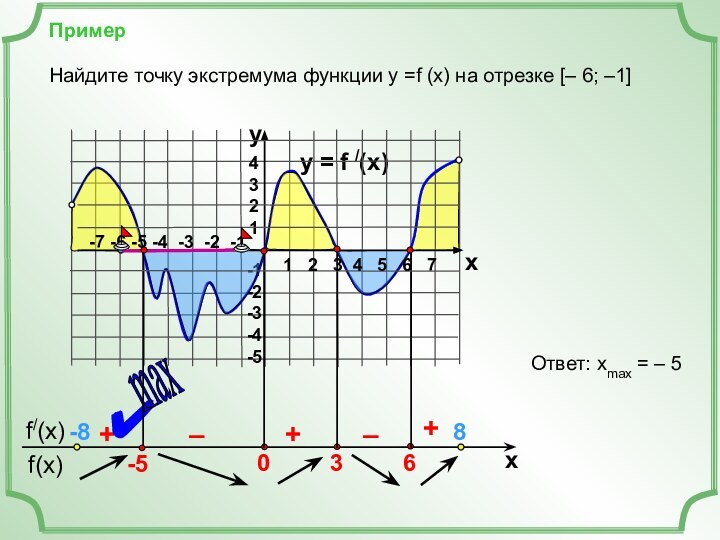
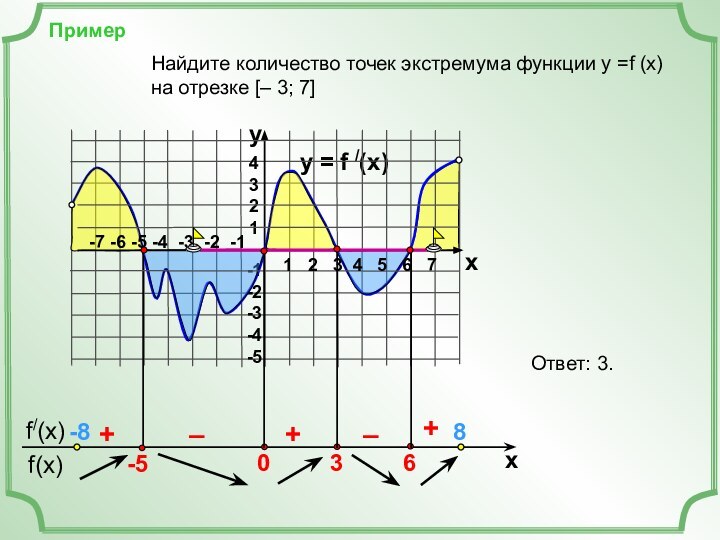
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
4
3
2
1
-1
-2
-3
-4
-5
y
x
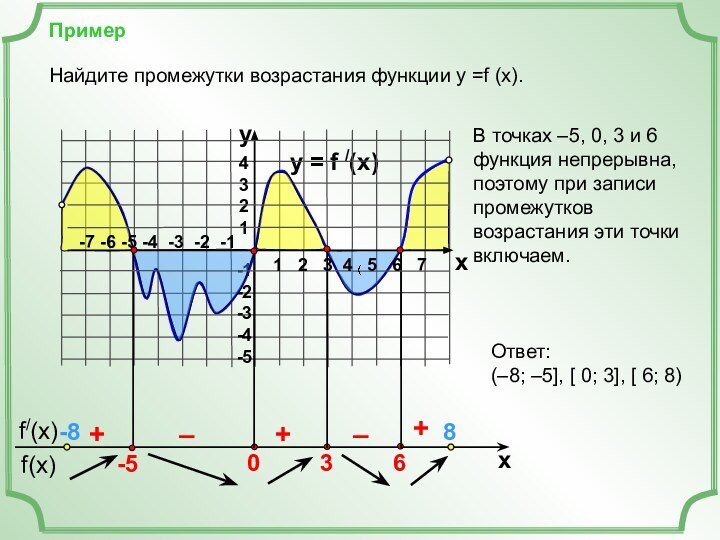
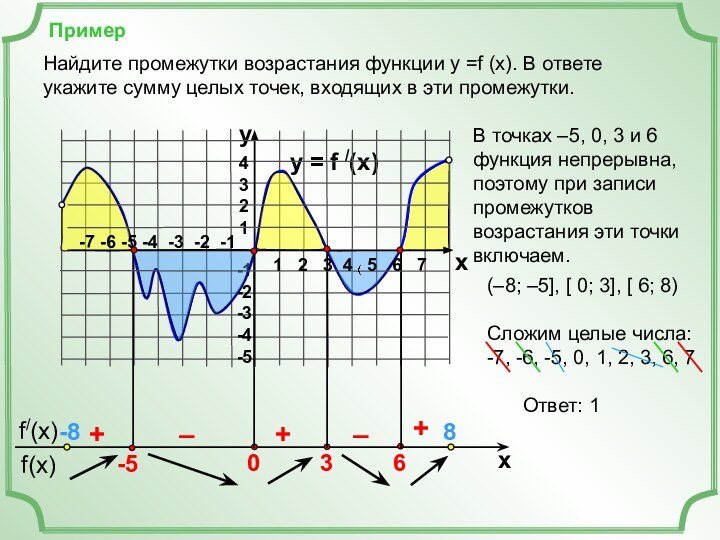
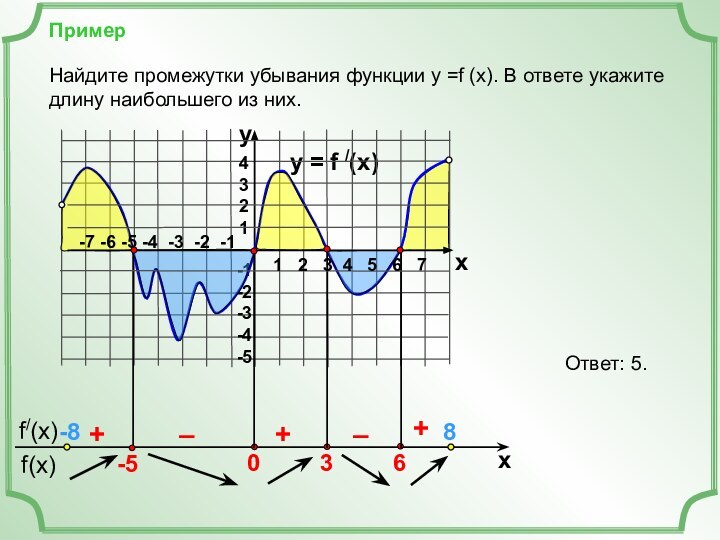
Найдем точки, в которых f /(x)=0 (это нули функции).
+
–
–
+
+

![Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции у](/img/tmb/15/1458626/150bd851d637735041b891b4abf24036-720x.jpg)
![Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [– 4; –1] функции у](/img/tmb/15/1458626/80b5f2cfe9087b2808649a48797dd2c4-720x.jpg)
![Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [ 0; 3] функции у](/img/tmb/15/1458626/86aa4b1d43e06ae478ea4a84f003ac5f-720x.jpg)
![Готовимся к ЕГЭ Примерy = f /(x) 4321-1-2-3-4-5yx+––++В какой точке отрезка [ 1; 4] функции у](/img/tmb/15/1458626/2a375bf7c5723d61dcf07d57340fb40e-720x.jpg)