- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Графический способ решения квадратных уравнений
Содержание
- 2. Графический способ решения уравнений состоит в построении
- 3. 1 случайПрямая и парабола касаются (имеют единственную общую точку), абсцисса точки касания – корень уравнения
- 4. 2 случайПрямая и парабола пересекаются в двух точках, абсциссы этих точек являются корнями уравнения.
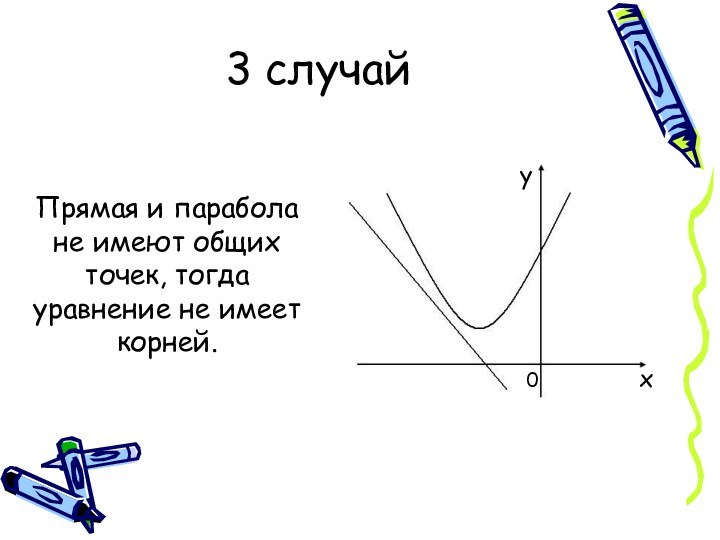
- 5. 3 случайПрямая и парабола не имеют общих точек, тогда уравнение не имеет корней.
- 6. ПримерРешите графически уравнение х²+1,5х-2,5=0. Решение. Перепишем
- 7. Задание на домРешите графически уравнение:а) х²=0б) 2х²+7=0в) х²-2х=0
- 8. Скачать презентацию
- 9. Похожие презентации
Графический способ решения уравнений состоит в построении на одной координатной плоскости графиков двух функций и нахождении абсцисс их точек пересечения (если такие точки есть). В случае квадратного уравнения строятся графики квадратичной и линейной функций – парабола





Слайд 3
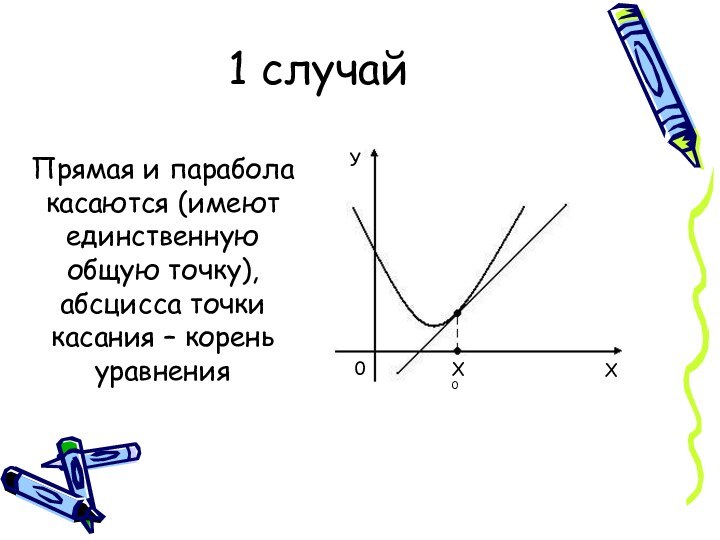
1 случай
Прямая и парабола касаются (имеют единственную общую
точку), абсцисса точки касания – корень уравнения
Слайд 4
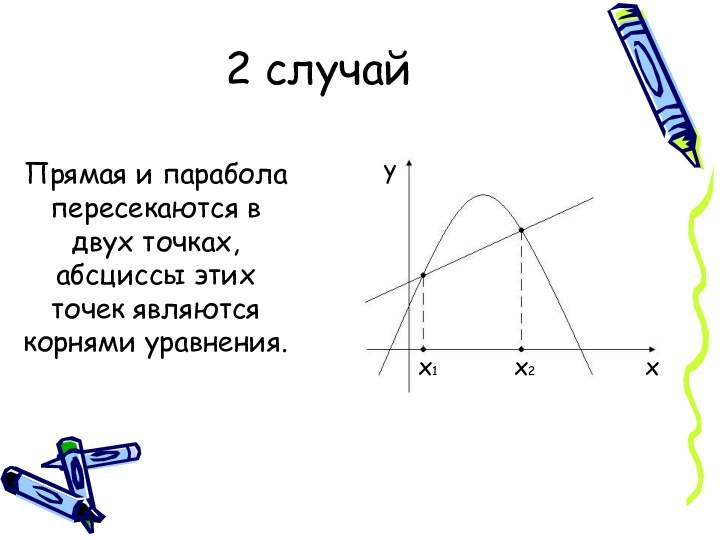
2 случай
Прямая и парабола пересекаются в двух точках,
абсциссы этих точек являются корнями уравнения.
Слайд 6
Пример
Решите графически уравнение х²+1,5х-2,5=0.
Решение. Перепишем уравнение в виде
х²=-1,5х+2,5. Рассмотрим функции у = х² и у = -1,5х+2,5. Построим
в одной координатной плоскости графики этих функций, найдем абсциссы их точек пересечения: х=-2,5, х=1. Эти числа являются корнями исходного уравнения.Ответ: х=-2,5, х=1.