- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Как найти объём тела
Содержание
- 2. Цель:Ввести понятие объема;Единицы измерения объема;Свойства объемовОбъем прямоугольного параллелепипедаОбъем прямой призмы, основанием которой является прямоугольный треугольник
- 3. Фигуры в пространстве имеют объемВеличина части пространства, занимаемого геометрическим телом , называется объемом этого тела
- 4. – Поиск формул, позволяющих вычислять объемы различных
- 5. На могильной плите Архимеда, как завещал ученый,
- 6. Объемы зерновых амбаров и других сооружений в
- 7. За единицу измерения объема принимается куб, ребро
- 8. Английские меры объемаБушель - 36,4 дм3Галлон -4,5
- 9. Русские меры объемаВедро - 12 дм3Бочка -
- 11. Свойства объемов2. Равные тела имеют равные объемыКакие
- 12. Равенство двух тел, в стереометрии определяется так
- 13. 20. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
- 14. Следствие:Объем куба с ребром равен
- 15. № 647Дано: тело R состоит из те
- 16. Объем прямоугольного параллелепипедаОбъем прямоугольного параллелепипеда равен произведению его измерений?Что такое измерения параллелепипеда?V=abc
- 17. Объем прямоугольного параллелепипеда. Теорема. Объем прямоугольного параллелепипеда
- 18. 2 сл.Пусть a, b, c –бесконечные десятичные
- 20. Итак, объем прямоугольного параллелепипеда равен произведению его
- 21. Дано: АВС - треугольная призма.Доказать: V призмы=
- 22. № 648, 649, 650, 651,652, 657Дома: №648,
- 23. №648 Найдите объем прямоугольного параллелепипеда, стороны основания
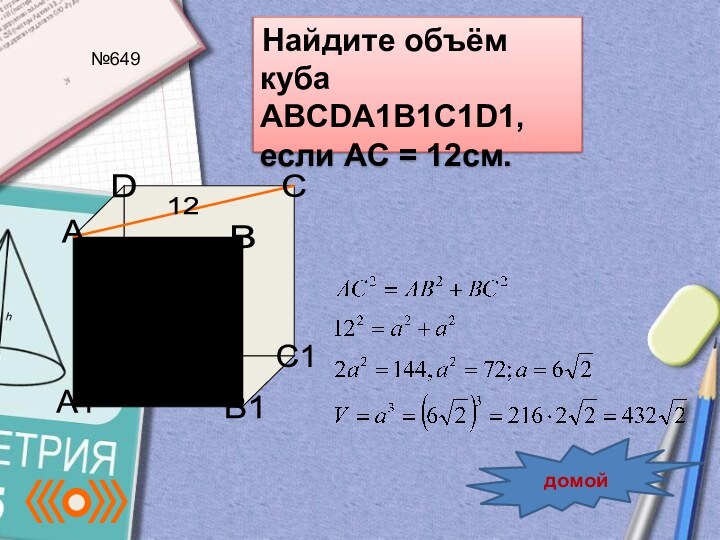
- 24. Найдите объём куба ABCDA1B1C1D1, если AC = 12см. №649домой
- 25. Кирпич имеет форму прямоугольного параллелепипеда с измерениями
- 26. № 650. Измерения прямоугольного параллелепипеда равны 8
- 27. Объем прямой призмы равен произведению основания на
- 28. Объем цилиндра равен произведению площади основания на
- 29. №659 (а), №660, 663 (а,в), 664, 666(а), 667, 669, 671(а)Дома: 672, 670, 662(б), 666(б), 671(б)
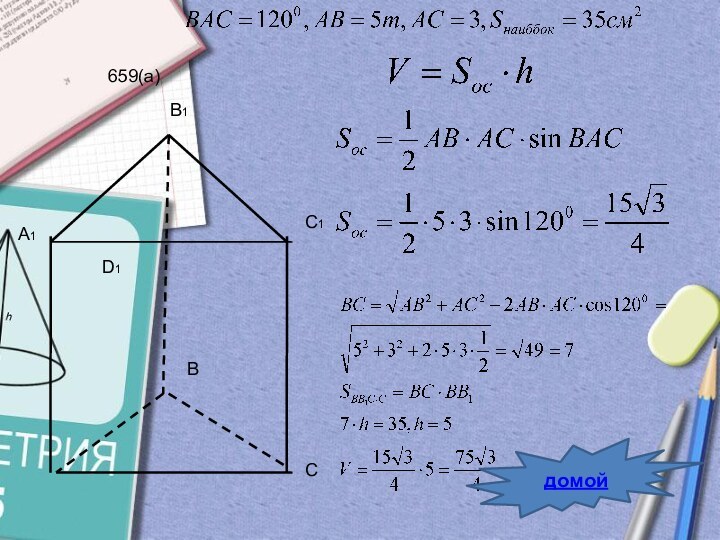
- 30. 659(а)домой
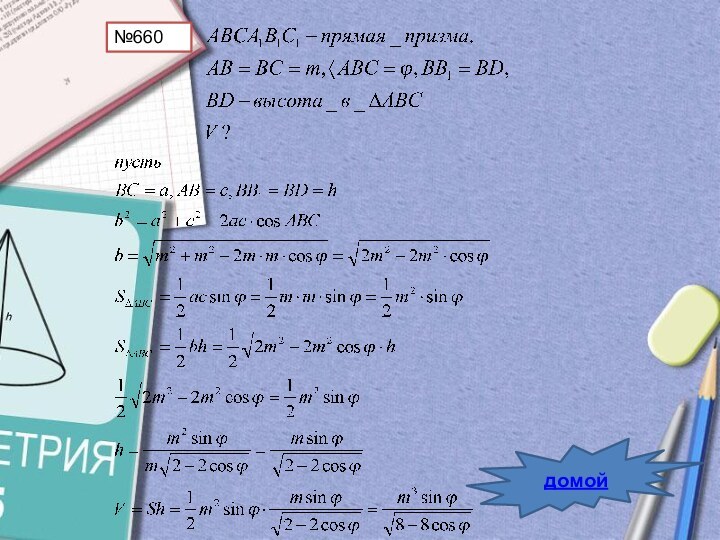
- 31. №660домой
- 32. №663домой
- 33. 664По теореме, обратной о трех перпендикулярахВдомой
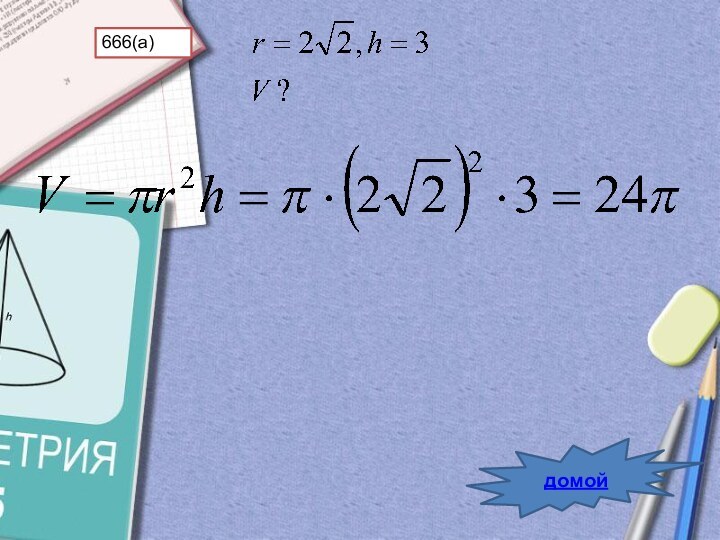
- 34. домой666(а)
- 35. домой667Дано: алюминиевый провод диаметром 4 мм имеет
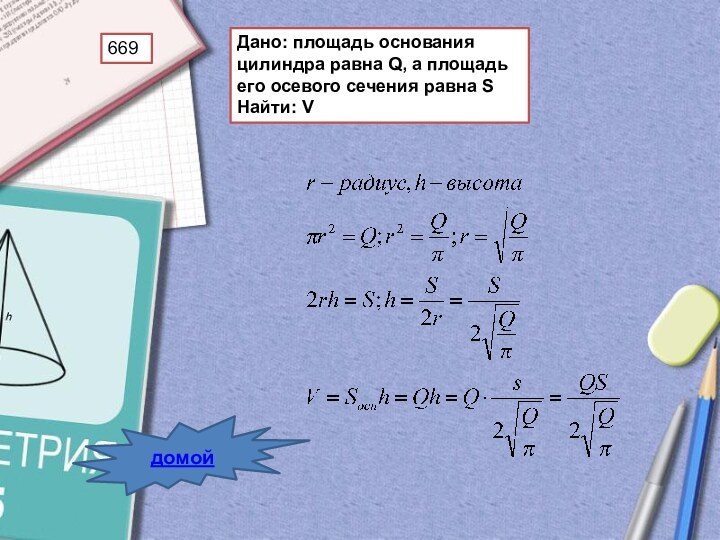
- 36. 669Дано: площадь основания цилиндра равна Q, а площадь его осевого сечения равна SНайти: Vдомой
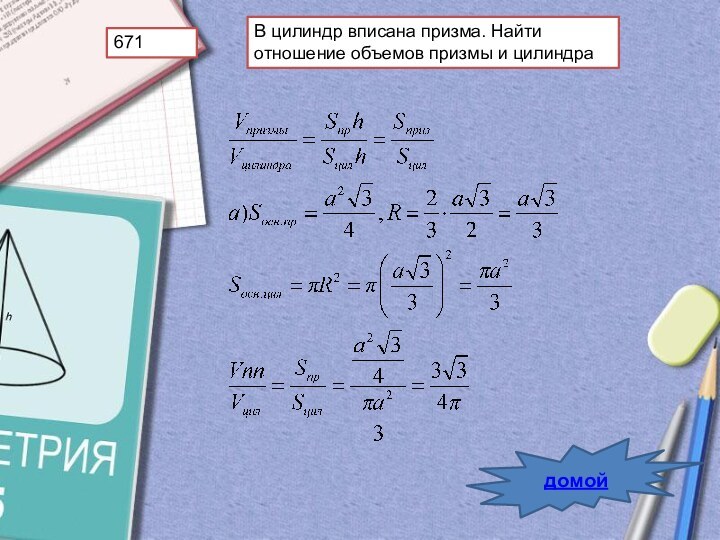
- 37. 671В цилиндр вписана призма. Найти отношение объемов призмы и цилиндрадомой
- 38. Скачать презентацию
- 39. Похожие презентации
Цель:Ввести понятие объема;Единицы измерения объема;Свойства объемовОбъем прямоугольного параллелепипедаОбъем прямой призмы, основанием которой является прямоугольный треугольник
Слайд 2
Цель:
Ввести понятие объема;
Единицы измерения объема;
Свойства объемов
Объем прямоугольного параллелепипеда
Объем
прямой призмы, основанием которой является прямоугольный треугольник
Слайд 3
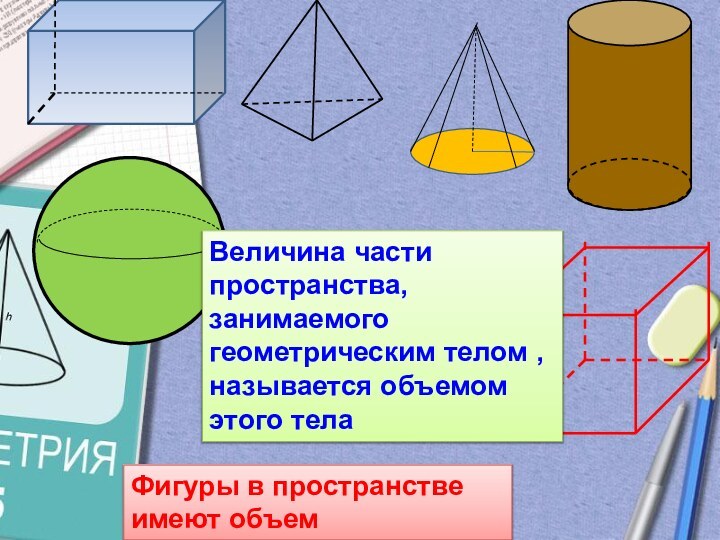
Фигуры в пространстве имеют объем
Величина части пространства, занимаемого
геометрическим телом , называется объемом этого тела
Слайд 4 – Поиск формул, позволяющих вычислять объемы различных тел,
был долог. В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются
правила для нахождения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды. Определять объемы призмы, пирамиды, цилиндра и конуса умели древние греки еще задолго до Архимеда. Но только он имел общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам ученый определил с помощью своего метода площади объемы почти всех тел, которые рассматривались в античной математике.Слайд 5 На могильной плите Архимеда, как завещал ученый, был
изображен цилиндр с вписанным шаром, а эпитафия говорила о
величайшем открытии Архимеда - о том, что объемы этих тел относятся как 3: 2.Когда Римский оратор и общественный деятель Цицерон, живший в 1 в. до н.э., был в Сицилии, он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.
АРХИМЕД (ок. 287-212 гг. до н.э.)
Слайд 6 Объемы зерновых амбаров и других сооружений в виде
кубов, призм и цилиндров египтяне и вавилоняне, китайцы индийцы
вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны только отдельные правила, найденные опытным путем. В более позднее время был найден общий подход к вычислению объемов многогранников.Среди замечательных греческих ученых 5-4 в до н.э., которые разрабатывали теорию объемов были Демокрит из Абдеры и Евдокс Книдский. Евклид не применяет термин «объем». Для него термин «куб» означает термин «объем» в 9 книге «Начал» изложены среди других теоремы об объемах.
Демокрит
Евдокс
Герон
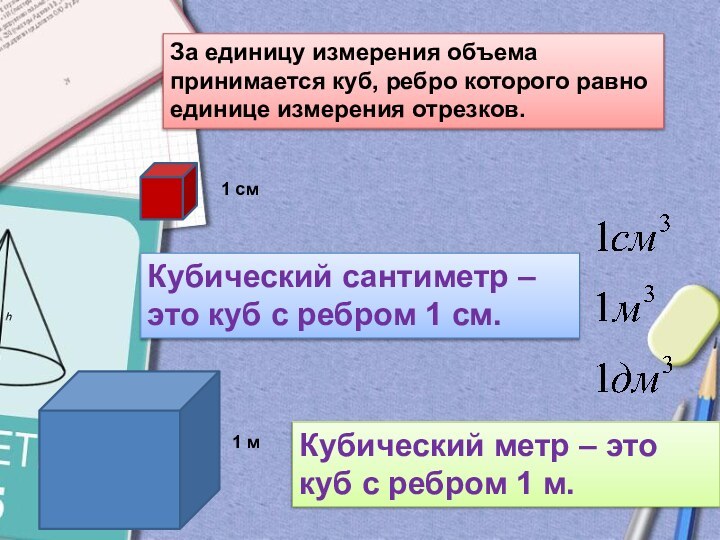
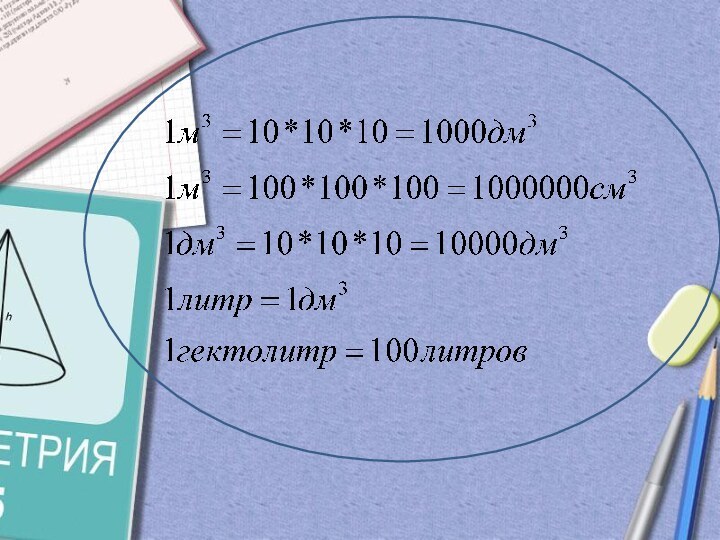
Слайд 7 За единицу измерения объема принимается куб, ребро которого
равно единице измерения отрезков.
Кубический сантиметр – это куб с
ребром 1 см. 1 см
Кубический метр – это куб с ребром 1 м.
1 м
Слайд 8
Английские меры объема
Бушель - 36,4 дм3
Галлон -4,5 дм3
Баррель
(сухой)-
115,628 дм3
Баррель (нефтяной)-
158,988 дм3
Английский баррель для сыпучих веществ 163,65
дм3
Слайд 9
Русские меры объема
Ведро - 12 дм3
Бочка - 490
дм3
Штоф - 1,23 дм3 = 10 чарок
Чарка -0,123 дм3=0,1
штофа= = 2 шкаликаШкалик -0,06 дм 3 = 0,5 чарки
Слайд 11
Свойства объемов
2. Равные тела имеют равные объемы
Какие тела
называются равными?
3. Если тело составлено из нескольких тел, то
его объем равен сумме объемов этих тел1. Объем тела есть неотрицательное число;
Если тело имеет объем V1 и содержится в теле, имеющем объем V2, то V1 < V2.
Слайд 12 Равенство двух тел, в стереометрии определяется так же,
как и в планиметрии:
Два тела называют равными, если их
можно совместить наложением.
Слайд 15
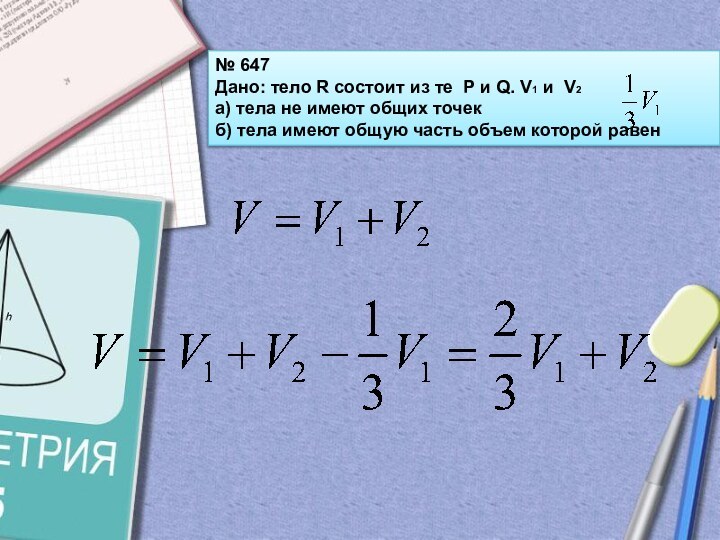
№ 647
Дано: тело R состоит из те P
и Q. V1 и V2
а) тела не имеют общих
точекб) тела имеют общую часть объем которой равен
Слайд 16
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его
измерений
?
Что такое измерения параллелепипеда
?
V=abc
Слайд 17 Объем прямоугольного параллелепипеда. Теорема. Объем прямоугольного параллелепипеда равен произведению
трех его измерений.
Дано: параллелепипед, а, b, c его измерения.V
- объемДоказать: V = abc.
Доказательство:
1 сл. Пусть а, b, c - конечные десятичные дроби ( n 1) . Числа а ·10n , b ·10 n, c·10 n - целые .
Разобьем каждое ребро параллелепипеда
на равные части длины и через
точки разбиения
проведем плоскости, перпендикулярные к
этому ребру. Параллелепипед разобьется
На abc·103 n равных кубов с ребром
Т.к.
объем каждого такого куба равен , то
объем всего параллелепипеда равен
Итак, V = abc.
Слайд 18 2 сл.Пусть a, b, c –бесконечные десятичные дроби.
Рассмотрим конечные десятичные дроби an, bn, cn
anbncnabc an’bn’cn’,
где Объем V параллелепипеда Р заключен между
Vn=anbncn и V’n= an’bn’cn’ т.е. anbncnV an’bn’cn’
Неограниченно увеличим n.
Тогда число an’bn’cn’ будет мало отличаться от числа anbncn .
V=abc.
Ч.т.д
Слайд 20 Итак, объем прямоугольного параллелепипеда равен произведению его измерений:
V=abc
Следствия:
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:
V=SоснhОбъем прямой призмы, основанием которой равен прямоугольный треугольник, равен произведению площади основания на высоту (доказать самостоятельно)
Слайд 21
Дано: АВС - треугольная призма.
Доказать: V призмы= S
ABC·h
Доказательство:
1. Достроим треугольную призму до прямоугольного параллелепипеда.
2. По
сл.2 V= 2 S ABC·h.3. (В1ВС) разбивает параллелепипед на две равные прямые призмы, одна из которых данная.
4. Следовательно V иск. равен половине объема параллелепипеда, т.е. V призмы= S ABC·h ч.т.д
Следствие 2. Объем прямой призмы, основанием
которой является прямоугольный треугольник,
равен произведению площади основания на высоту.
Слайд 22
№ 648, 649, 650, 651,652, 657
Дома: №648, 657
– дорешать
№655
Знать: единицы измерения объемов, выражать единицы через другие,
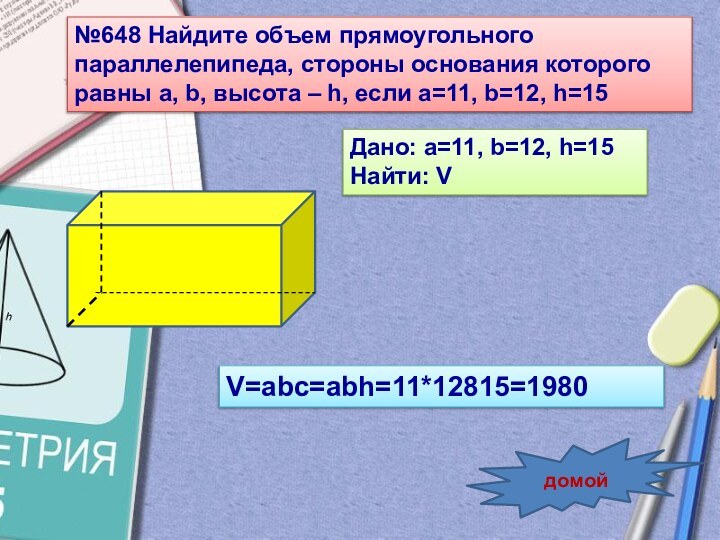
свойства объемов, формулы вычисления прямоугольного параллелепипеда, стр.150 – доказать 2 случайСлайд 23 №648 Найдите объем прямоугольного параллелепипеда, стороны основания которого
равны a, b, высота – h, если a=11, b=12,
h=15Дано: a=11, b=12, h=15
Найти: V
V=abc=abh=11*12815=1980
домой
Слайд 25 Кирпич имеет форму прямоугольного параллелепипеда с измерениями 25
см, 12 см и 6,5 см. Плотность кирпича равна
1,8 г/см3. Найдите его массу.
домой
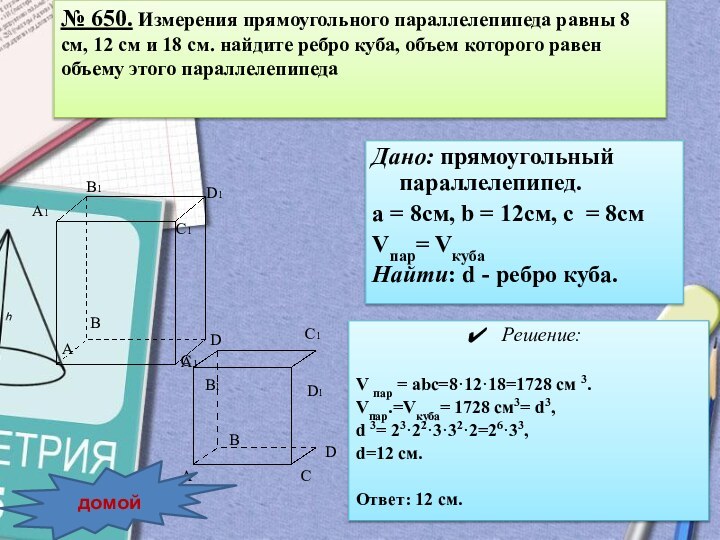
Слайд 26 № 650. Измерения прямоугольного параллелепипеда равны 8 см,
12 см и 18 см. найдите ребро куба, объем
которого равен объему этого параллелепипедаДано: прямоугольный параллелепипед.
а = 8см, b = 12см, с = 8см
Vпар= Vкуба
Найти: d - ребро куба.
домой
Решение:
V пар = abc=8·12·18=1728 cм 3.
Vпар.=Vкуба= 1728 cм3= d3,
d 3= 23·22·3·32·2=26·33,
d=12 см.
Ответ: 12 см.
Слайд 27
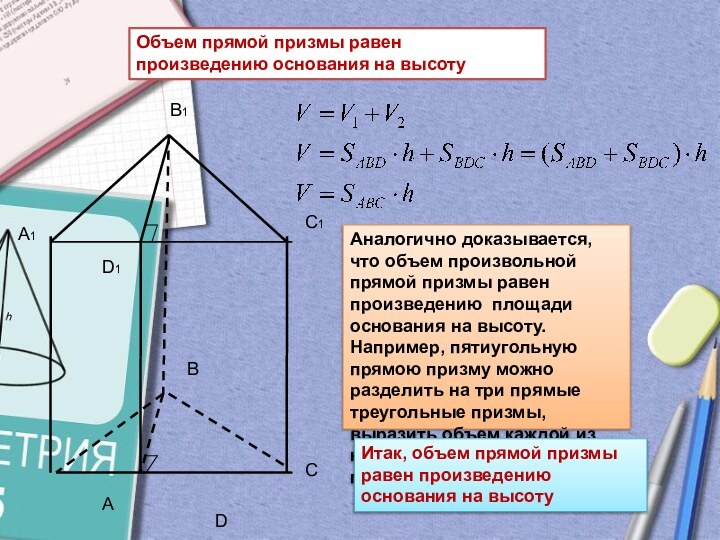
Объем прямой призмы равен произведению основания на высоту
A
D
Аналогично
доказывается, что объем произвольной прямой призмы равен произведению площади
основания на высоту. Например, пятиугольную прямою призму можно разделить на три прямые треугольные призмы, выразить объем каждой из них и найти объем всей призмы.Итак, объем прямой призмы равен произведению основания на высоту
Слайд 28 Объем цилиндра равен произведению площади основания на высоту.
Впишем в данный цилиндр Р радиуса r и высоты
h правильную n-угольную призму Fn, а в эту призму впишем цилиндр Pn. Пусть объемы цилиндров Р и Pn равны V и Vn, через rn –радиус цилиндра Pn.Чему равен объем призмы Fn?
Слайд 29 №659 (а), №660, 663 (а,в), 664, 666(а), 667,
669, 671(а)
Дома: 672, 670, 662(б), 666(б), 671(б)
Слайд 35
домой
667
Дано: алюминиевый провод диаметром 4 мм имеет массу
6,8 кг. Найти длину провода, если плотность алюминия равна
2,6 грамм на куб. см
Слайд 36
669
Дано: площадь основания цилиндра равна Q, а площадь
