изучению нового материала
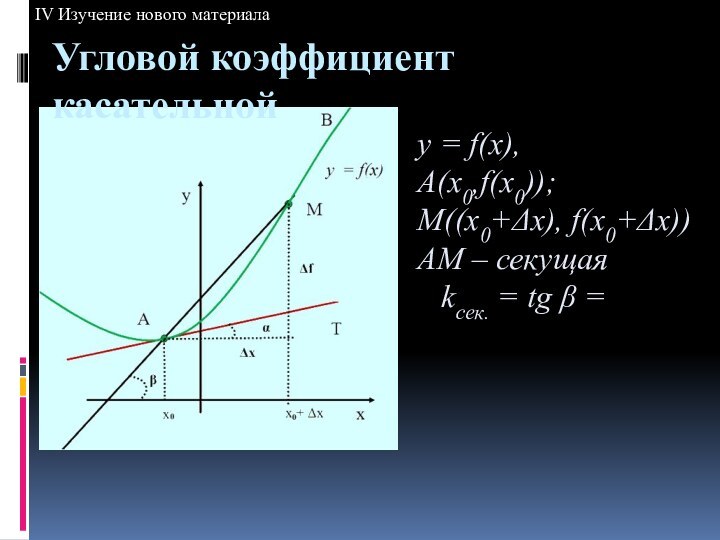
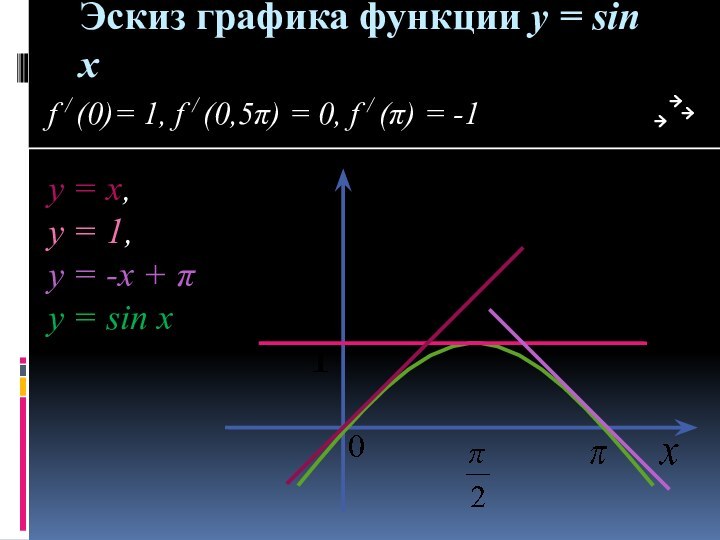
IV Изучение нового материала
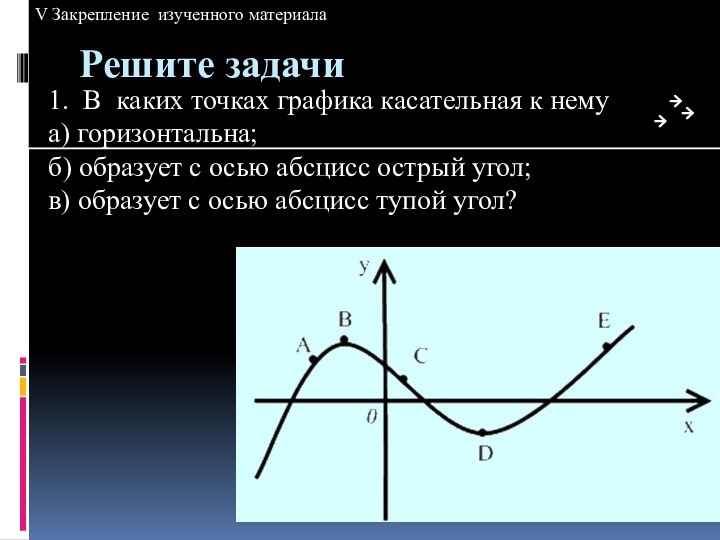
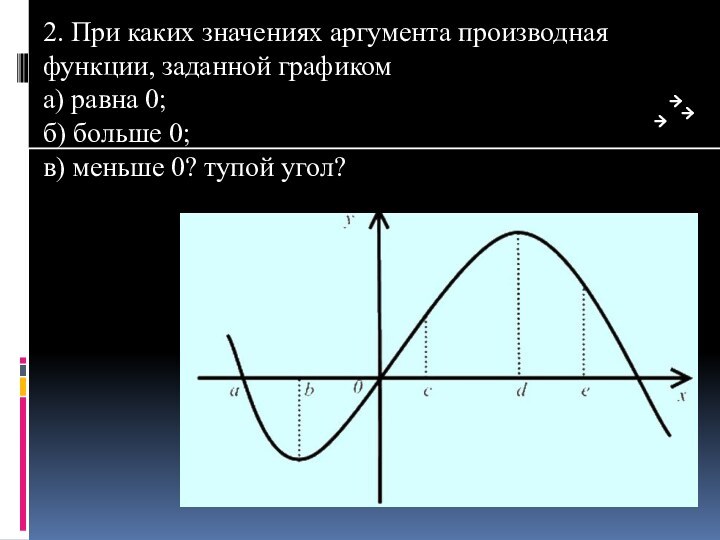
V Закрепление изученного материала
VI Подведение итогов урока
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





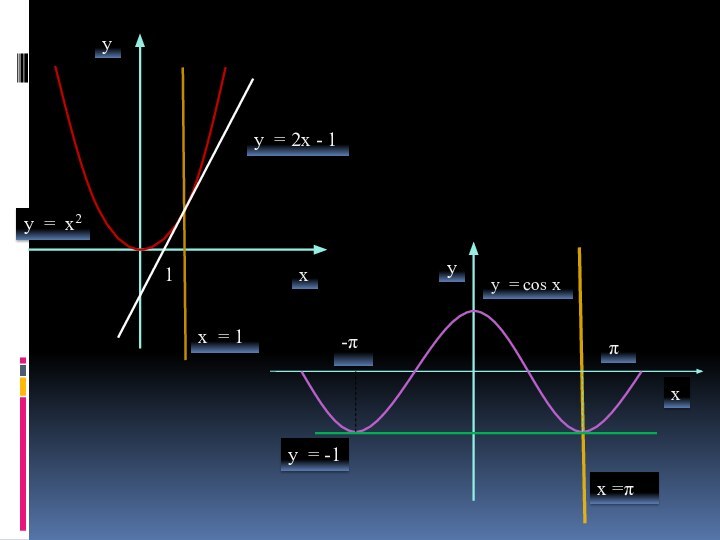















III Подготовка к изучению нового материала
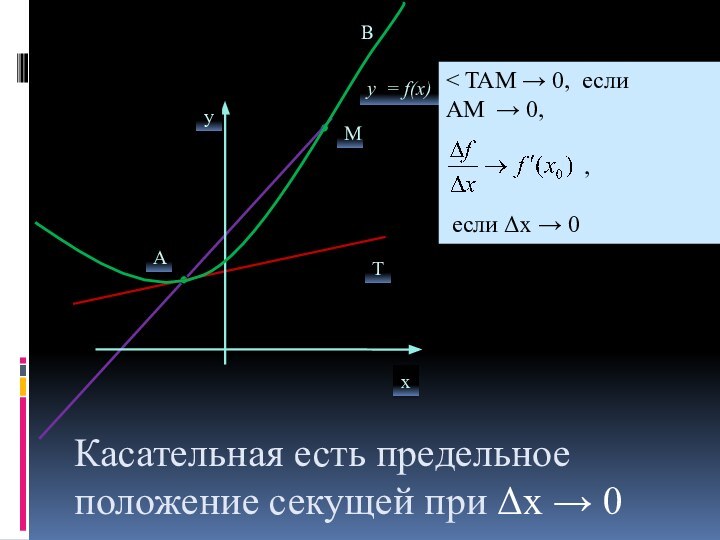
Касательная есть предельное положение секущей при Δх → 0
Определение касательной
V Закрепление изученного материала
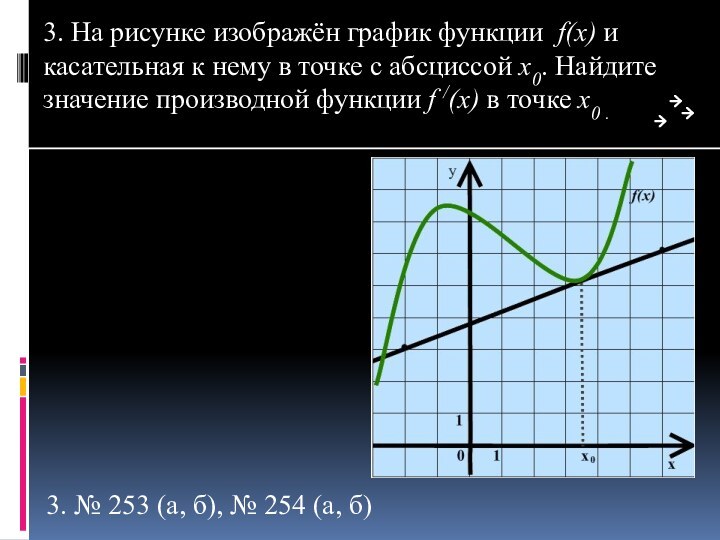
3. № 253 (а, б), № 254 (а, б)
2. По ординате точки касания.
Составить уравнение касательной в точке
Графика с ординатой y0 = 1.
3. Заданного направления.
Написать уравнения касательной к графику
y = x3 – 2x + 7, параллельной прямой у = х.
4. Условия касания графика и прямой.
При каких b прямая y = 0,5x + b является касательной к графику функции ?
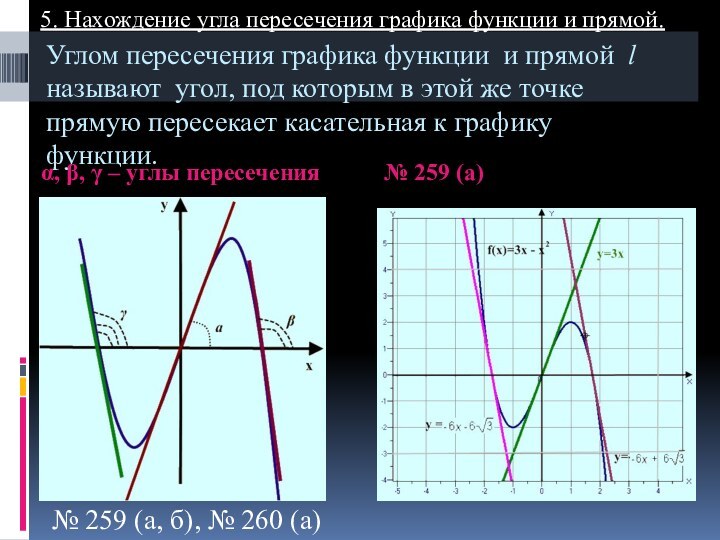
α, β, γ – углы пересечения
№ 259 (а)
№ 259 (а, б), № 260 (а)
5. Нахождение угла пересечения графика функции и прямой.
Домашнее задание