Презентация на тему Кенгуру

Содержание

2. Виды заданий:
3. 1.Задания на классификацию
4. Пример: 1. На рисунке отмечены вершины
5. 2.Наглядные задачи (Что
6. Пример наглядной задачи Поль выиграл
7. 3. Логика Задачи этой
8. Пример задачи на логику: 1.
9. Пример на логику: 2. В группе
10. Комбинаторика Для решения этих задач нужно
11. Пример комбинаторной задачи 1. Сколькими способами
12. Конструкции Чтобы решить эти задачи, нужно
13. Пример задачи на конфигурацию 1. 1. Какое
14. 2. Правильную пирамиду с квадратом в основании
15. Скачать презентацию
16. Похожие презентации

Виды заданий: 1. Классификация 2. Наглядные задачи (Что мы видим на картинке?) 3. Логика 4. Комбинаторика 5. Конструкции

Выполнила: Панфилова Ольга Юрьевна. Учитель математики. МКОУ «Петуховская средняя общеобразовательная школа №1»

1.Задания на классификацию В каждой из следующих

Пример: 1. На рисунке отмечены вершины и центр правильного шестиугольника. Назовем

Пример наглядной задачи Поль выиграл футболку, на которой написано слово

3. Логика Задачи этой серии требуют умения рассуждать, доказывать,

Пример задачи на логику: 1. Какие из следующих трех утверждений

Пример на логику: 2. В группе 40% ребят имеют плохое зрение.

Комбинаторика Для решения этих задач нужно подсчитать количество комбинаций (наборов) каких-то

Пример комбинаторной задачи 1. Сколькими способами можно расположить 4 шашки на

Конструкции Чтобы решить эти задачи, нужно либо придумать какую-то подходящую конструкцию,

Пример задачи на конфигурацию 1. 1. Какое наименьшее количество клеток нужно дополнительно

2. Правильную пирамиду с квадратом в основании разрезали пополам плоскостью, а потом

Слайды презентации

Слайд 2 Виды заданий: 1. Классификация 2.

Виды заданий: 1. Классификация 2. Наглядные задачи (Что

Наглядные задачи (Что мы видим на картинке?) 3. Логика 4. Комбинаторика 5.

Конструкции

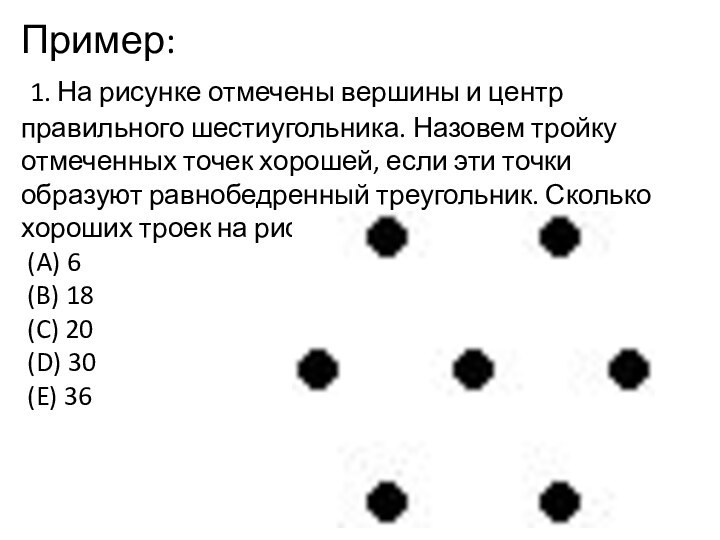
Слайд 3 1.Задания на классификацию В каждой

1.Задания на классификацию В каждой из следующих задач

из следующих задач надо подсчитать количество каких-то объектов: геометрических

фигур, стрелок, точек и т.д. Прежде, чем начать такой подсчет, полезно разбить эти объекты на группы и сначала провести нужные подсчеты по каждой группе отдельно.

Слайд 4 Пример: 1. На рисунке отмечены вершины и центр

правильного шестиугольника. Назовем тройку отмеченных точек хорошей, если эти

точки образуют равнобедренный треугольник. Сколько хороших троек на рисунке? (A) 6 (B) 18 (C) 20 (D) 30 (E) 36

Слайд 5 2.Наглядные задачи (Что мы

видим

на картинке?) Чтобы решить эти задачи обычно достаточно просто внимательно рассмотреть рисунок. А иногда надо придумать нужный рисунок самостоятельно.

Слайд 6 Пример наглядной задачи
Поль выиграл футболку, на которой

написано слово . Он надел ее и подошел к

зеркалу. Какую запись он увидел?
(A) (B) (C) (D) (E)

Слайд 7 3. Логика Задачи этой серии требуют умения

рассуждать, доказывать, а иногда и просто перебрать варианты: «Что

будет, если …».

Слайд 8 Пример задачи на логику: 1. Какие из следующих

трех утверждений верны? (1)Сумма двух отрицательных чисел всегда

отрицательна. (2)Сумма одного отрицательного числа и одного положительного числа всегда положительна. (3)Сумма одного отрицательного числа и двух положительных чисел всегда положительна. (А) все неверны (В) только (1) (С) только (1) и (3) (D) только (2) и (3) (E) все три верны

Слайд 9 Пример на логику: 2. В группе 40% ребят имеют

плохое зрение. 70% из них носят очки, остальные 30%

носят контактные линзы. Общее число ребят в очках - 21. Что верно: (A) 30 человек имеет плохое зрение (B) 30 человек имеет хорошее зрение (C) всего в группе 100 человек (D) 10 человек носят линзы (E) ни один ответ не подходит