Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Коэффициенты квадратной функции

Содержание

2. Предисловие.В данном проекте автор специально не использовал
3. Общие сведения.У=ах2+вх+с-общий вид квадратной функции.Квадратное уравнение выглядит
4. Корнями квадратного уравнения будем считать точки пересечения
5. Корень уравнения будет один, если парабола касается
6. Коэффициент «а».Коэффициент а – это коэффициент икса
7. Коэффициент «а».Если а>0 (а - положительный), ветви параболы направлены вверх.Если а
8. Коэффициент «а».Для более удобных рассуждений и работы
9. Коэффициент «с».Коэффициент с - это свободный член
10. Коэффициент «с».Если коэффициент«с» положительный и а>0, то
11. Коэффициент «с».Если коэффициент«с» отрицательныйи а>0, то корни
12. Коэффициент «с».Если коэффициентс=0, то один корень равен
13. Коэффициент «в».Коэффициент в - это коэффициент икса
14. Коэффициент «в».Корень квадратного уравнения находящийся дальше от
15. Коэффициент «в».Коэффициент «в» всегда имеет знак противоположный
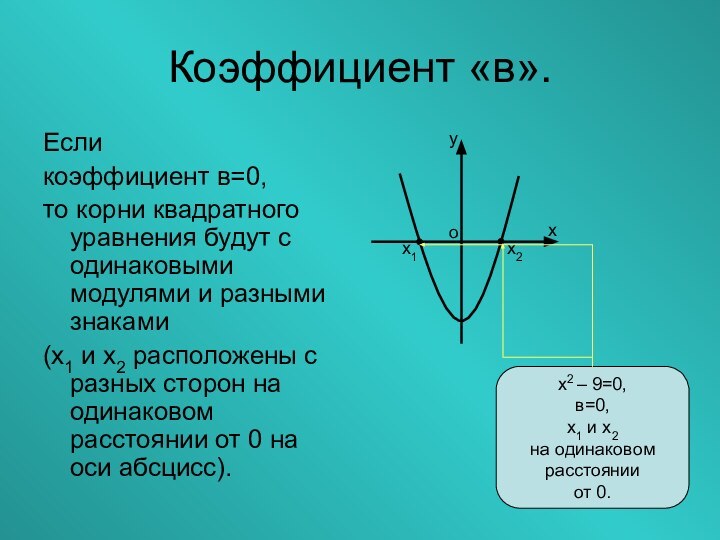
16. Коэффициент «в».Если коэффициент в=0,то корни квадратного уравнения
17. Дискриминант.При помощи дискриминанта можно установить количество корней
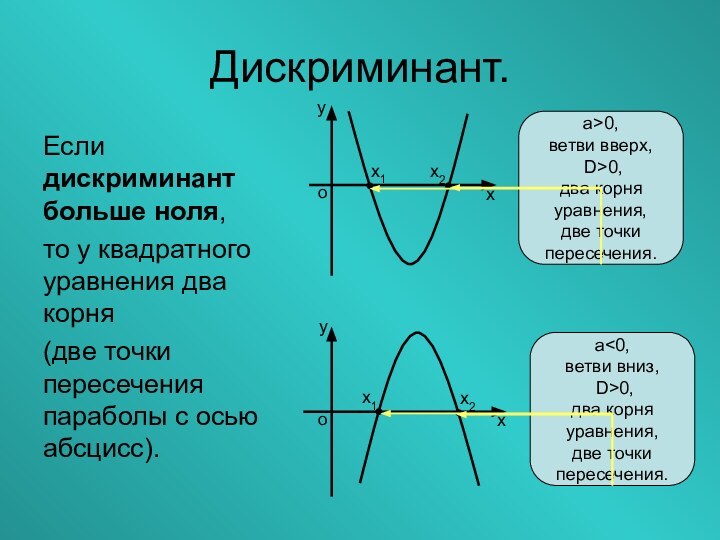
18. Дискриминант.Если дискриминант больше ноля,то у квадратного уравнения
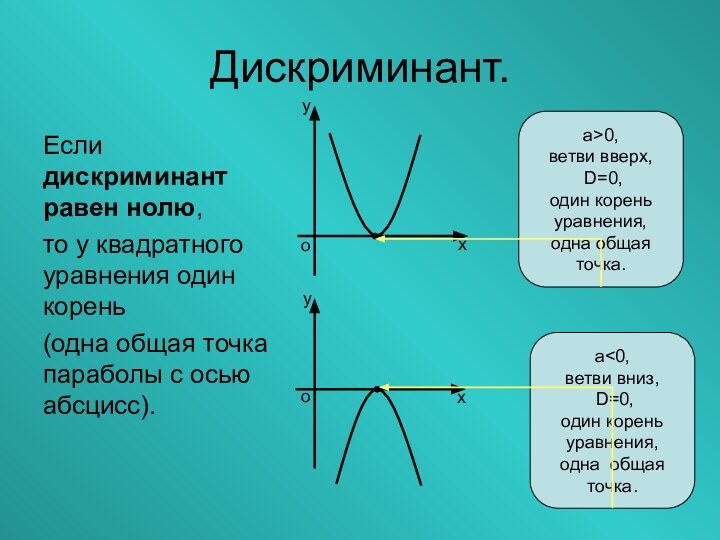
19. Дискриминант.Если дискриминант равен нолю,то у квадратного уравнения
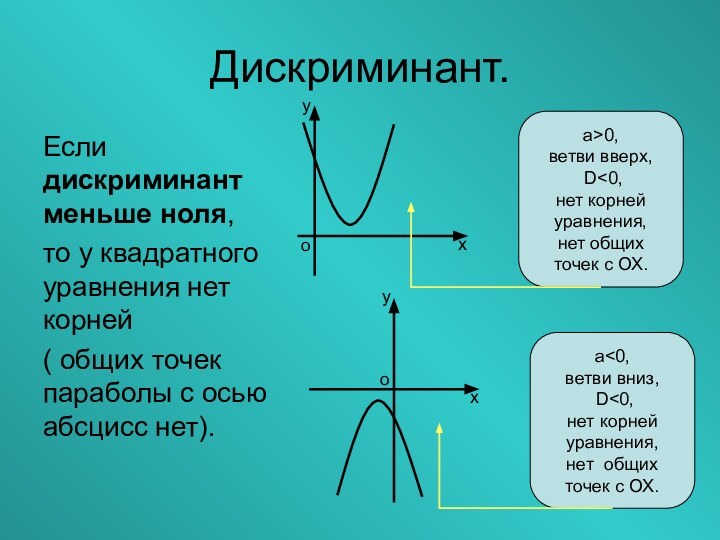
20. Дискриминант.Если дискриминант меньше ноля,то у квадратного уравнения
21. Пример.Какое из уравнений соответствует данному рисунку?а) 5х2
22. Пример.2х2 – 6х – 2=0 - это
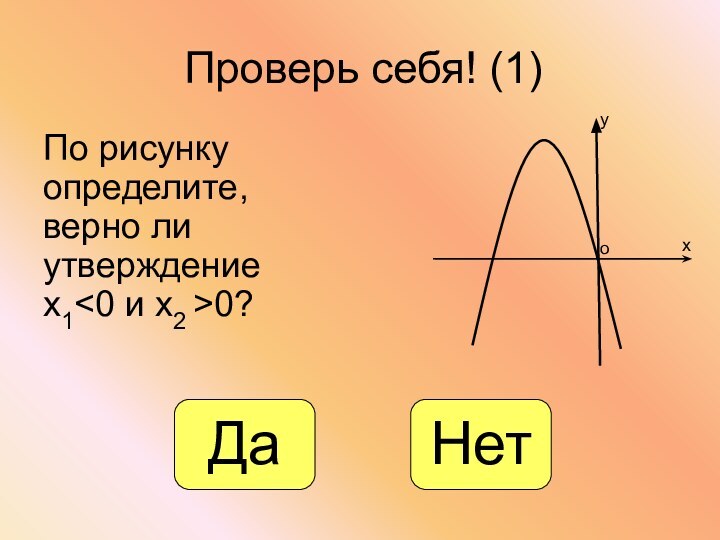
23. Проверь себя! (1)По рисунку определите, верно ли утверждение х10?хуоДаНет
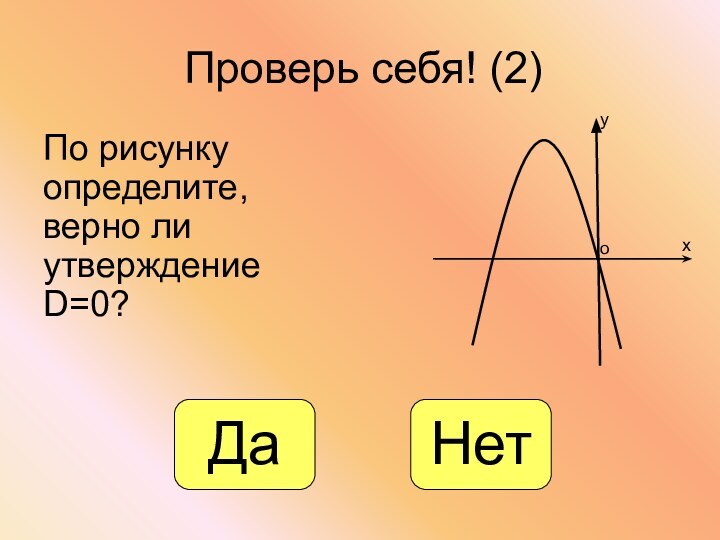
24. Проверь себя! (2)По рисунку определите, верно ли утверждение D=0?хуоДаНет
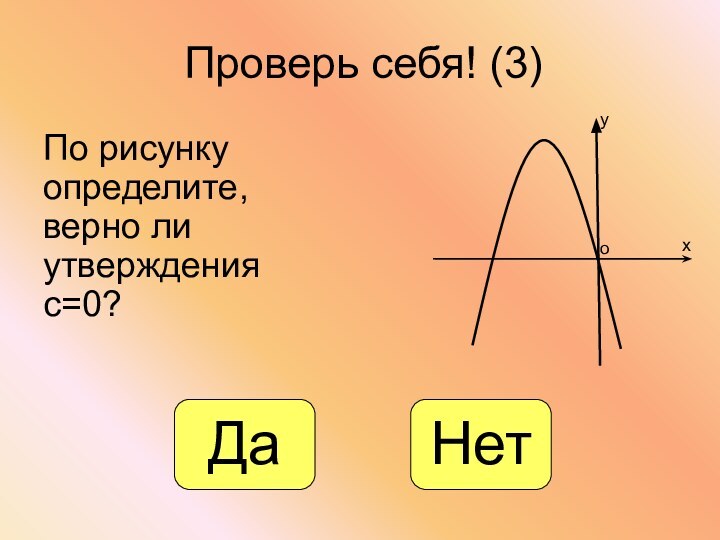
25. Проверь себя! (3)По рисунку определите, верно ли утверждения с=0?хуоДаНет
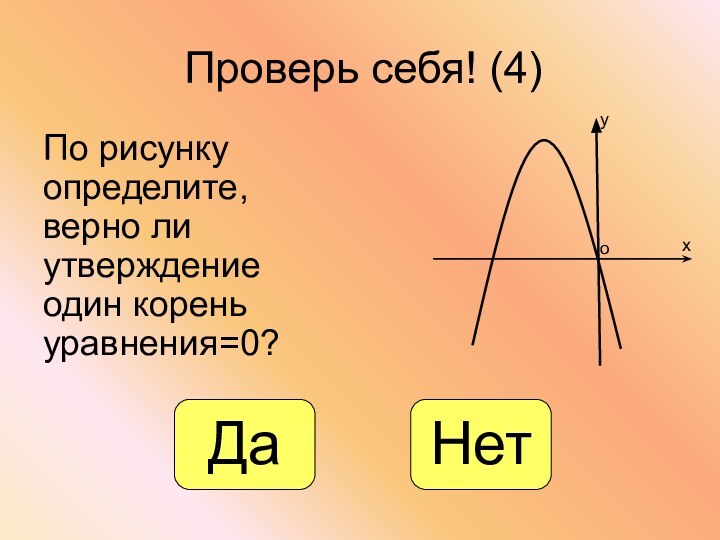
26. Проверь себя! (4)По рисунку определите, верно ли утверждение один корень уравнения=0?хуоДаНет
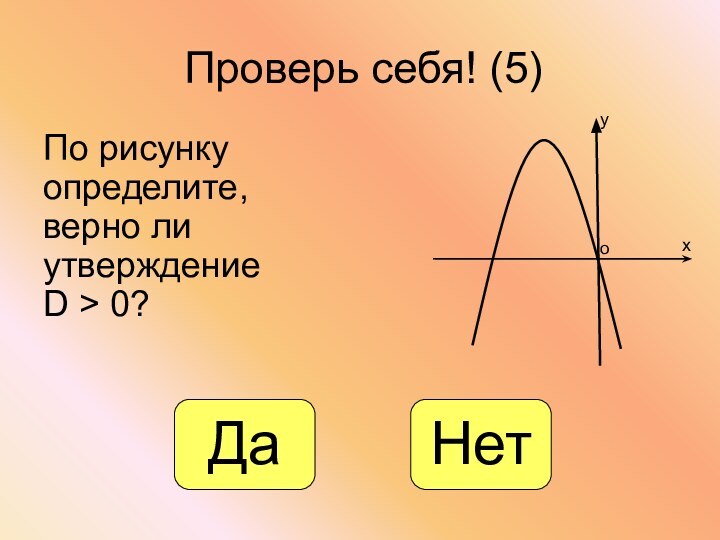
27. Проверь себя! (5)По рисунку определите, верно ли утверждение D > 0?хуоДаНет
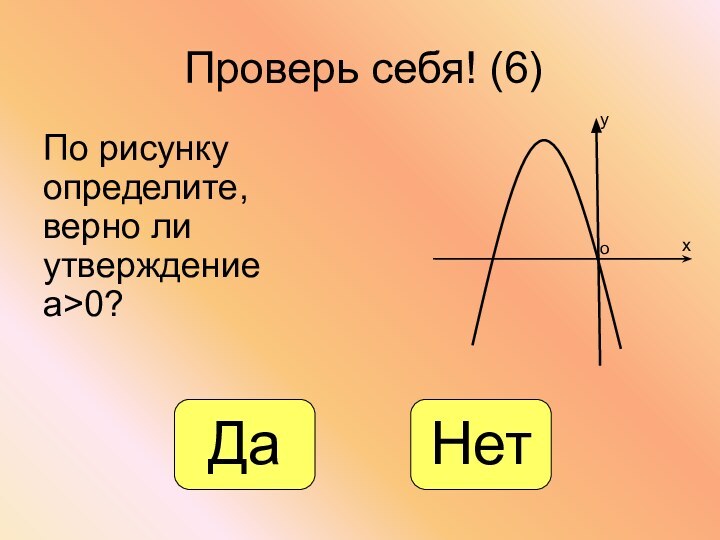
28. Проверь себя! (6)По рисунку определите, верно ли утверждение а>0?хуоДаНет
29. Конец.Литература: учебники алгебры для средней школы авторских
30. Примечание.Свои замечания и предложения высылайте на адрес
31. Скачать презентацию
32. Похожие презентации

Предисловие.В данном проекте автор специально не использовал теоретическое обоснование, а только выводы на их основе. Для более глубокого и полного изучения этой темы рекомендовано использовать пособия по математике для средней школы.

Главная
Математика
Коэффициенты квадратной функции

Элементы квадратного уравнения.Для подготовки к ГИА.Учитель математики Барсуков А. А.МБОУ Краснодесантская СОШ

Предисловие.В данном проекте автор специально не использовал теоретическое обоснование, а только выводы

Общие сведения.У=ах2+вх+с-общий вид квадратной функции.Квадратное уравнение выглядит так: ах2+вх+с=0.Где «а» коэффициент при

Корнями квадратного уравнения будем считать точки пересечения параболы-графика квадратной функции с осью

Корень уравнения будет один, если парабола касается оси ОХ (абсцисс) в одной

Коэффициент «а».Коэффициент а – это коэффициент икса в квадрате. От него зависит

Коэффициент «а».Если а>0 (а - положительный), ветви параболы направлены вверх.Если а

Коэффициент «а».Для более удобных рассуждений и работы с коэффициентами «в» и «с»

Коэффициент «с».Коэффициент с - это свободный член (число без х).При помощи коэффициента

Коэффициент «с».Если коэффициент«с» положительный и а>0, то корни уравнения имеют одинаковые знаки

Коэффициент «с».Если коэффициент«с» отрицательныйи а>0, то корни уравнения имеют разные знаки (х1

Коэффициент «с».Если коэффициентс=0, то один корень равен нолю(график параболы проходит через начало

Коэффициент «в».Коэффициент в - это коэффициент икса (число перед х).При помощи коэффициента

Коэффициент «в».Корень квадратного уравнения находящийся дальше от ноля имеет больший модуль.0С большим

Коэффициент «в».Коэффициент «в» всегда имеет знак противоположный корню с большим модулем при

Коэффициент «в».Если коэффициент в=0,то корни квадратного уравнения будут с одинаковыми модулями и

Дискриминант.При помощи дискриминанта можно установить количество корней квадратного уравнения или их отсутствие.Дискриминант

Дискриминант.Если дискриминант больше ноля,то у квадратного уравнения два корня(две точки пересечения параболы

Дискриминант.Если дискриминант равен нолю,то у квадратного уравнения один корень(одна общая точка параболы

Дискриминант.Если дискриминант меньше ноля,то у квадратного уравнения нет корней( общих точек параболы

Пример.Какое из уравнений соответствует данному рисунку?а) 5х2 + 2х + 4=0б) –

Пример.2х2 – 6х – 2=0 - это уравнение соответствует рисунку,так как:D=44, D>0,

Проверь себя! (1)По рисунку определите, верно ли утверждение х10?хуоДаНет

Проверь себя! (2)По рисунку определите, верно ли утверждение D=0?хуоДаНет

Проверь себя! (3)По рисунку определите, верно ли утверждения с=0?хуоДаНет

Проверь себя! (4)По рисунку определите, верно ли утверждение один корень уравнения=0?хуоДаНет

Проверь себя! (5)По рисунку определите, верно ли утверждение D > 0?хуоДаНет

Проверь себя! (6)По рисунку определите, верно ли утверждение а>0?хуоДаНет

Конец.Литература: учебники алгебры для средней школы авторских групп А. Г. Мордковича, Г.

Примечание.Свои замечания и предложения высылайте на адрес 2010Свои замечания и предложения высылайте

Неправильно.Возврат к примеру.Переход к лекциям.

Слайды презентации

Слайд 2 Предисловие.
В данном проекте автор специально не использовал теоретическое

Предисловие.В данном проекте автор специально не использовал теоретическое обоснование, а только

обоснование, а только выводы на их основе. Для более

глубокого и полного изучения этой темы рекомендовано использовать пособия по математике для средней школы.

Слайд 3 Общие сведения.
У=ах2+вх+с
-общий вид квадратной функции.
Квадратное уравнение выглядит так:

Общие сведения.У=ах2+вх+с-общий вид квадратной функции.Квадратное уравнение выглядит так: ах2+вх+с=0.Где «а» коэффициент

ах2+вх+с=0.
Где «а» коэффициент при х2, «в» - при х,

«с» свободный член.

У=6х2 – 4х + 7

Коэффициент а=6

Коэффициент в = – 4

Коэффициент с=7

Слайд 4
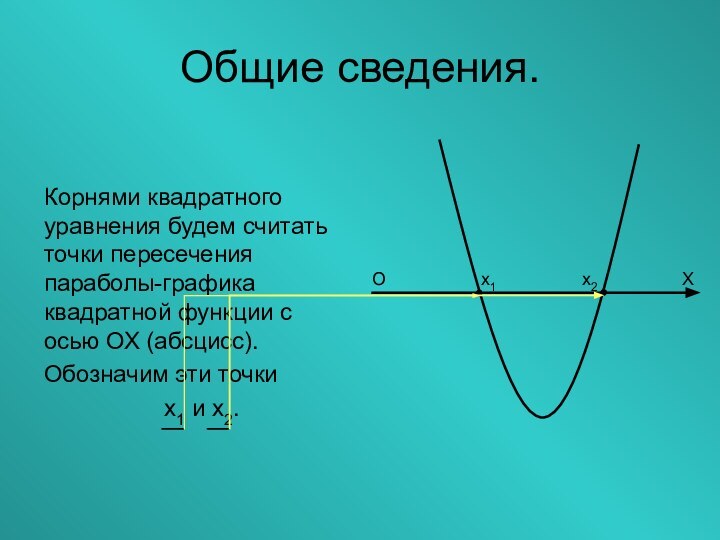
Корнями квадратного уравнения будем считать точки пересечения параболы-графика

Корнями квадратного уравнения будем считать точки пересечения параболы-графика квадратной функции с

квадратной функции с осью ОХ (абсцисс).
Обозначим эти точки
х1

и х2.

О х1 х2 Х

Общие сведения.

Слайд 5 Корень уравнения будет один, если парабола касается оси

Корень уравнения будет один, если парабола касается оси ОХ (абсцисс) в

ОХ (абсцисс) в одной точке.

О

Общие сведения.

Слайд 6 Коэффициент «а».
Коэффициент а – это коэффициент икса в

Коэффициент «а».Коэффициент а – это коэффициент икса в квадрате. От него

квадрате. От него зависит направление ветвей параболы (вверх или

вниз).

3х2 + 5х – 9=0

коэффициент а = 3

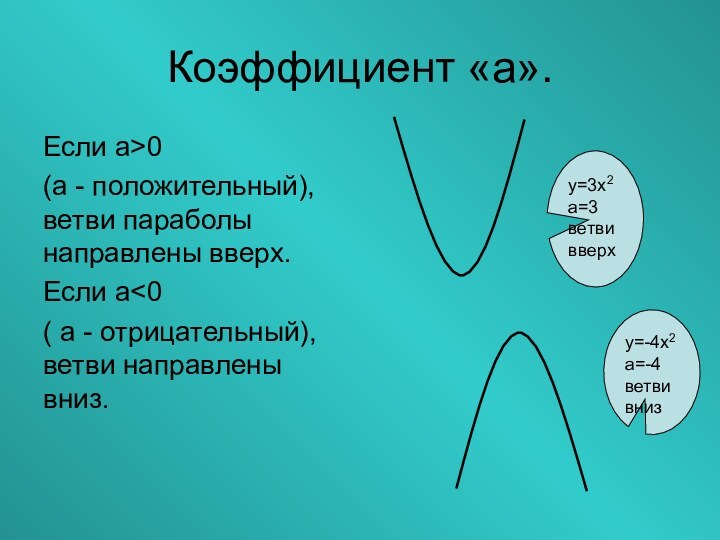
Слайд 7 Коэффициент «а».
Если а>0
(а - положительный), ветви параболы

направлены вверх.
Если а

вниз.

у=3х2
а=3
ветви
вверх

у=-4х2
а=-4
ветви вниз

Слайд 8 Коэффициент «а».
Для более удобных рассуждений и работы с

Коэффициент «а».Для более удобных рассуждений и работы с коэффициентами «в» и

коэффициентами «в» и «с» надо обратить внимание на знак

коэффициента «а».
Он должен быть больше ноля. Если «а» отрицательный, то поменяем все знаки в квадратном уравнении умножив его на минус один.

Пример.
–2х2 + 4х – 7=0 |•(-1),
2х2 – 4х + 7=0
– все знаки поменяли
на противоположные,
коэффициент «а»
теперь положительный,
начинаем работу с
коэффициентами «в» и «с».

Слайд 9 Коэффициент «с».
Коэффициент с - это свободный член (число

Коэффициент «с».Коэффициент с - это свободный член (число без х).При помощи

без х).
При помощи коэффициента «с» можно сделать вывод о

знаках корней уравнения (х1 и х2).

3х2 + 5х – 9=0

коэффициент с = –9

12 + 3х2 – 5х=0

коэффициент с = 12

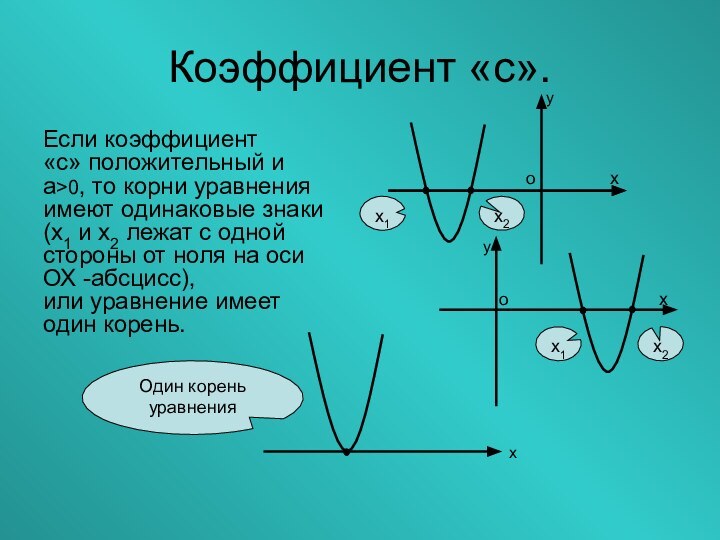
Слайд 10 Коэффициент «с».
Если коэффициент
«с» положительный и а>0, то корни

Коэффициент «с».Если коэффициент«с» положительный и а>0, то корни уравнения имеют одинаковые

уравнения имеют одинаковые знаки (х1 и х2 лежат с

одной стороны от ноля на оси ОХ -абсцисс),
или уравнение имеет один корень.

Один корень уравнения

х1

х2

х1

х2

о х

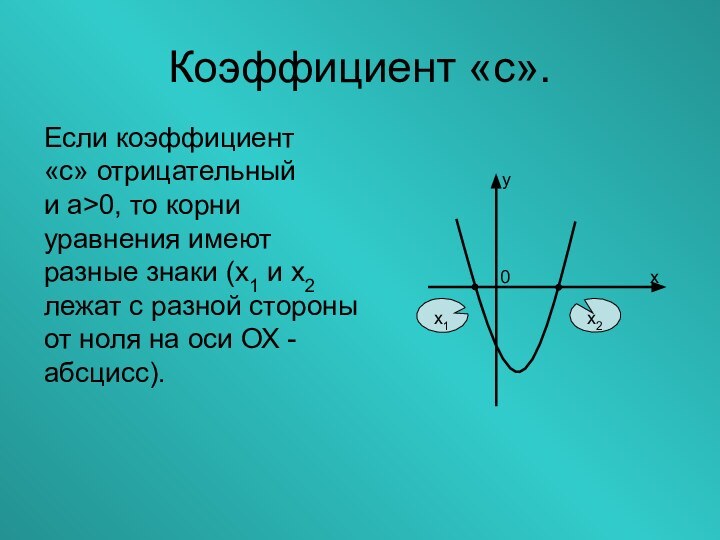
Слайд 11 Коэффициент «с».
Если коэффициент
«с» отрицательный
и а>0, то корни уравнения

Коэффициент «с».Если коэффициент«с» отрицательныйи а>0, то корни уравнения имеют разные знаки

имеют разные знаки (х1 и х2 лежат с разной

стороны от ноля на оси ОХ -абсцисс).

0 х

х1

х2

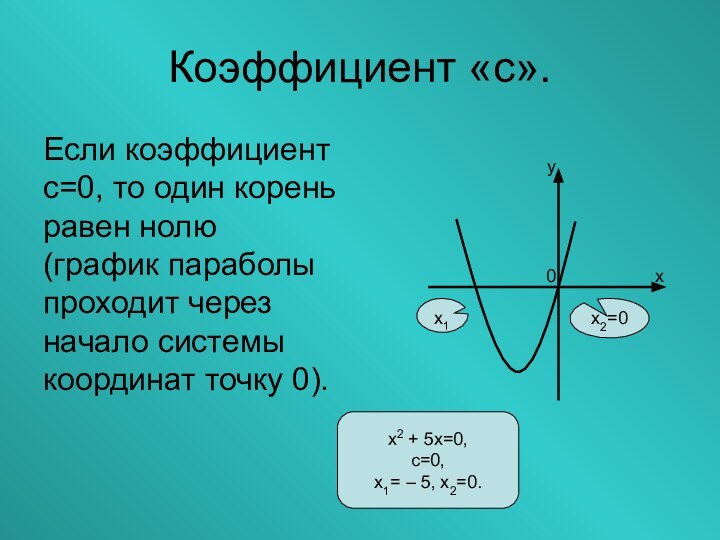
Слайд 12 Коэффициент «с».
Если коэффициент
с=0, то один корень равен нолю
(график

Коэффициент «с».Если коэффициентс=0, то один корень равен нолю(график параболы проходит через

параболы проходит через начало системы координат точку 0).
0

х1

х2=0

х2 + 5х=0,
с=0,
х1= – 5, х2=0.

Слайд 13 Коэффициент «в».
Коэффициент в - это коэффициент икса (число

Коэффициент «в».Коэффициент в - это коэффициент икса (число перед х).При помощи

перед х).
При помощи коэффициента «в» можно сделать вывод о

знаке корня квадратного уравнения с большим модулем (х1 или х2).

3х2 + 5х – 9=0

коэффициент в = 5

– 5х + 12 + 3х2=0

коэффициент в = –5

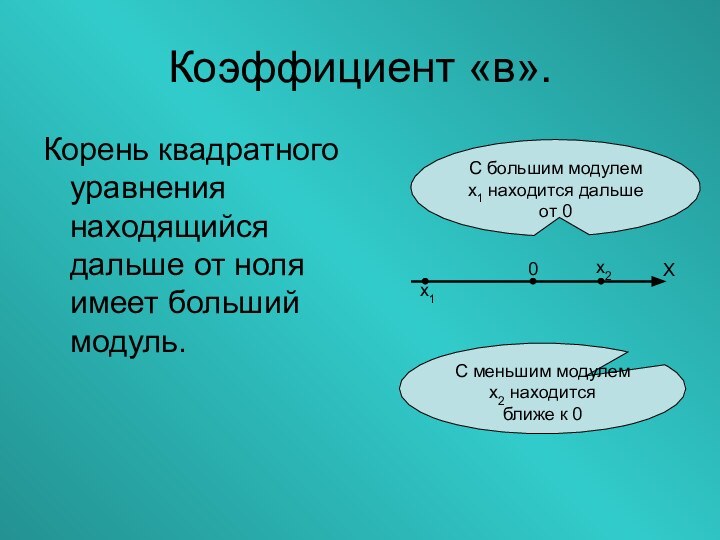
Слайд 14 Коэффициент «в».
Корень квадратного уравнения находящийся дальше от ноля

Коэффициент «в».Корень квадратного уравнения находящийся дальше от ноля имеет больший модуль.0С

имеет больший модуль.

0

С большим модулем х1 находится дальше от

С меньшим модулем х2 находится
ближе к 0

х2

х1

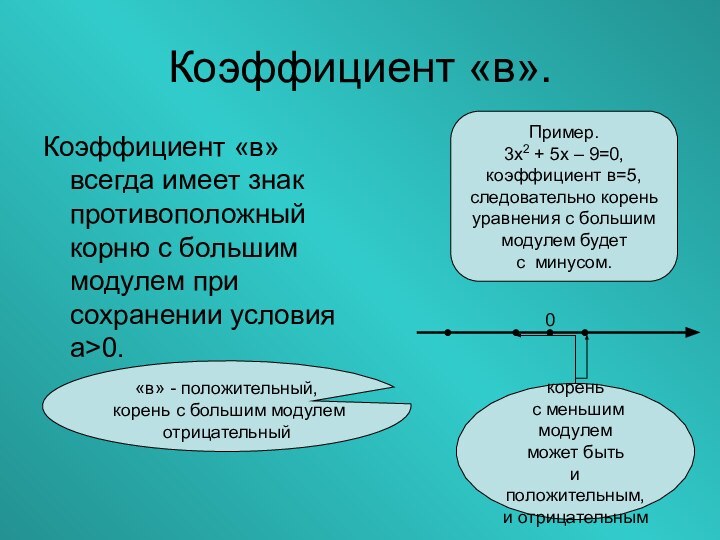
Слайд 15 Коэффициент «в».
Коэффициент «в» всегда имеет знак противоположный корню

Коэффициент «в».Коэффициент «в» всегда имеет знак противоположный корню с большим модулем

с большим модулем при сохранении условия а>0.
Пример.
3х2 + 5х

– 9=0,
коэффициент в=5,
следовательно корень
уравнения с большим
модулем будет
с минусом.

«в» - положительный,
корень с большим модулем отрицательный

корень
с меньшим модулем
может быть
и положительным,
и отрицательным

Слайд 16 Коэффициент «в».
Если
коэффициент в=0,
то корни квадратного уравнения будут

Коэффициент «в».Если коэффициент в=0,то корни квадратного уравнения будут с одинаковыми модулями

с одинаковыми модулями и разными знаками
(х1 и х2

расположены с разных сторон на одинаковом расстоянии от 0 на оси абсцисс).

х1

х2

х2 – 9=0,
в=0,
х1 и х2
на одинаковом
расстоянии
от 0.

Слайд 17 Дискриминант.
При помощи дискриминанта можно установить количество корней квадратного

Дискриминант.При помощи дискриминанта можно установить количество корней квадратного уравнения или их

уравнения или их отсутствие.
Дискриминант вычисляется по формуле D=в2 –

4ас.

Пример.
3х2 + 5х – 9=0,
а = 3, в = 5, с = – 9,
D=в2 – 4ас,
D=52 – 4•3•(-9)=
=25+108=133.

Дискриминант D=133

Слайд 18 Дискриминант.
Если дискриминант больше ноля,
то у квадратного уравнения два

Дискриминант.Если дискриминант больше ноля,то у квадратного уравнения два корня(две точки пересечения

корня
(две точки пересечения параболы с осью абсцисс).

а>0,
ветви вверх,
D>0,
два

корня
уравнения,
две точки
пересечения.

а<0,
ветви вниз,
D>0,
два корня
уравнения,
две точки
пересечения.

х1

х2

Слайд 19 Дискриминант.
Если дискриминант равен нолю,
то у квадратного уравнения один

Дискриминант.Если дискриминант равен нолю,то у квадратного уравнения один корень(одна общая точка

корень
(одна общая точка параболы с осью абсцисс).

а>0,
ветви вверх,
D=0,
один

корень
уравнения,
одна общая
точка.

а<0,
ветви вниз,
D=0,
один корень
уравнения,
одна общая
точка.

Слайд 20 Дискриминант.
Если дискриминант меньше ноля,
то у квадратного уравнения нет

Дискриминант.Если дискриминант меньше ноля,то у квадратного уравнения нет корней( общих точек

корней
( общих точек параболы с осью абсцисс нет).

у
х
о
о
у
х
а>0,
ветви вверх,

D<0,
нет корней
уравнения,
нет общих
точек с ОХ.

а<0,
ветви вниз,
D<0,
нет корней
уравнения,
нет общих
точек с ОХ.

Слайд 21 Пример.
Какое из уравнений соответствует данному рисунку?
а) 5х2 +

2х + 4=0
б) – 2х2 – 6х – 3=0
в)

2х2 + 6х – 4=0
г) 2х2 – 6х + 2=0
д) 2х2 – 6х – 2=0

D = – 76, D<0, нет корней,
нет пересечения
с ОХ.

а = – 2, а<0, ветви
направлены вниз.

в=6, корень
с большим модулем
отрицательный.

с=2, с>0, корни с одинаковыми знаками, точки пересечения с одной стороны от 0.

Это уравнение соответствует рисунку.

Слайд 22 Пример.
2х2 – 6х – 2=0 - это уравнение

соответствует рисунку,
так как:
D=44, D>0, два корня уравнения, две точки

пересечения;
а=2, а>0, ветви направлены вверх;
в = –6, корень уравнения с большим модулем положительный.
с = –2, с<0, корни уравнения с разными знаками, х1 и х2 стоят с разных сторон от 0;

два корня уравнения
с разных сторон от 0.

ветви направлены вверх

корень с большим модулем положительный