Слайд 2
Список литературы
Е. С. Вентцель, Л.А. Овчаров, Теория вероятностей
и ее инженерные приложения. – М: Высшая школа, 2000г.
Е. С. Вентцель, Л.А. Овчаров, Задачи и упражнения по теории вероятностей. М: Высшая школа, 2000г.
Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие — 12-е изд., перераб.- М.: Высшее образование, 2006.
Г.В. Горелова, И.А. Кацко, Теория вероятностей и математическая статистика в примерах и задачах с применением EXCEL.- Ростов-на-Дону.: Феникс, 2001.
Ю. Е. Шишмарев, Дискретная математика. Конспект лекций, Ч.2. ВГУЭС, 2002г.
Слайд 3
Исторические сведения
Возникновение теории вероятностей как науки относят к

средним векам и связывают с первыми попыткам математического анализа
азартных игр (орлянка, кости, рулетка). Самые ранние работы учёных в области теории вероятностей относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх, Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей. Решением тех же задач занимался и Христиан Гюйгенс. Его работа, в которой вводятся основные понятия теории вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год).
Важный вклад в теорию вероятностей внёс Якоб Бернулли (доказательство закона больших чисел в простейшем случае независимых испытаний). В первой половине XIX века теория вероятностей начинает применяться к анализу ошибок наблюдений. Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.
Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Слайд 4
Комбинаторика.
Принципы сложения и умножения
Слайд 5
Комбинаторика
Комбинаторика – раздел математики, посвященный подсчету количеств разных
комбинаций элементов некоторого, обычно конечного, множества
Комбинаторика возникла в
XVI веке. Первоначально комбинаторные задачи касались в основном азартных игр. Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Паскаль и Ферма. Дальнейшие развитие комбинаторики связано с именами Якова Бернулли, Лейбница и Эйлера.
Слайд 6
Принципы комбинаторики
Принцип сложения
Основные принципы комбинаторики:
Принцип сложения.
Принцип умножения.
Принцип сложения
Задача
1: В классе 7 девочек и 8 мальчиков. Сколькими
способами можно выбрать 1 человека для работы у доски?
Решение: Для работы у доски мы можем выбрать девочку 7 способами или мальчика 8 способами.
Общее число способов равно 7+8=15.
Задача 2: В классе 7 человек имеют «5» по математике, 9 человек – «5» по истории, 4 человека имеют «5» и по математике и по истории. Сколько человек имеют пятерку по математике или по истории?
Решение: Так как 4 человека входят и в семерку отличников по математике и в девятку отличников по истории, то сложив «математиков» и «историков», мы дважды учтем этих четверых, поэтому вычтя их один раз из суммы, получим результат 7+9-4=12.
Итак, 12 человек имеют пятерку по математике или по истории.
Слайд 7
Принцип сложения
Принцип сложения 1: Если объект a можно
получить n способами, объект b можно получить m способами
и эти способы различны, то объект «a или b» можно получить n+m.
Принцип сложения 2: Если объект a можно получить n способами, объект b можно получить m способами, то объект «a или b» можно получить n+m-k способами, где k – это количество повторяющихся способов.
Слайд 8
Принцип умножения
Задача: На вершину горы ведут 5 дорог.
Сколькими способами можно подняться на гору и спуститься с
нее?
Решение: Для каждого варианта подъема на гору существует 5 вариантов спуска с горы. Значит всего способов подняться на гору и спуститься с нее 5∙5=25.
Принцип умножения: если объект a можно получить n способами, объект b можно получить m способами, то объект «a и b» можно получить m∙n способами.
Слайд 9
Задачи
1) Из 10 коробок конфет, 8 плиток шоколада
и 12 пачек печенья выбирают по одному предмету для
новогоднего подарка. Сколькими способами это можно сделать?
Решение. Коробку конфет можно выбрать 10 способами, шоколад – 8, печенье – 12 способами. Всего по принципу умножения получаем способов.
Слайд 10
Задачи
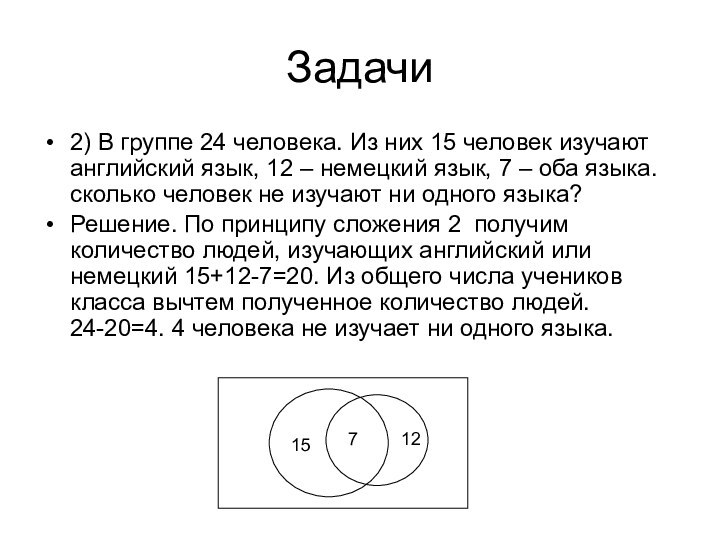
2) В группе 24 человека. Из них 15
человек изучают английский язык, 12 – немецкий язык, 7
– оба языка. сколько человек не изучают ни одного языка?
Решение. По принципу сложения 2 получим количество людей, изучающих английский или немецкий 15+12-7=20. Из общего числа учеников класса вычтем полученное количество людей. 24-20=4. 4 человека не изучает ни одного языка.
Слайд 12
Задачи
1) Из двух спортивных обществ, насчитывающих по 20
боксеров каждое,
надо выделить по одному боксеру для участия в
состязаниях. Сколькими способами это можно сделать?
Решение. По принципу умножения
Слайд 13
Задачи
2) Сколькими способами можно выбрать гласную и согласную
букву в слове «экзамен»?
Решение. В слове «экзамен» 3 гласные
буквы и 4 согласные. По принципу умножения
Слайд 14
Задачи
3) В классе 20 человек, из них 9
человек изучают язык программирования Бейсик, и 8 человек изучают
Паскаль. Сколько человек не изучают языки программирования, если известно, что других языков в этом классе не изучают и каждый человек знает не более одного языка программирования?
Решение. По принципу сложения получим, что 9+8=17
человек изучают языки программирования.
20-17=3 человека не изучают языки программирования.
Слайд 15
Задачи
4) От дома до школы существует 6 маршрутов.
Сколькими способами можно дойти до школы и вернуться, если
дорога «туда» и «обратно» идет по разных маршрутам?
Решение. По принципу умножения
Слайд 16
Задачи
5) Из 3 экземпляров учебника алгебры, 5 экземпляров
учебника геометрии и 7 экземпляров учебника истории нужно выбрать
по одному экземпляру каждого учебника. Сколькими способами это можно сделать?
Решение. По принципу умножения
Слайд 17
Задачи
6) В корзине лежат 15 яблок и 10
апельсинов. Яша выбирает из нее яблоко или апельсин, после
чего Полина берет яблоко и апельсин. В каком случае Полина имеет большую свободу выбора: если Яша взял яблоко или если он взял апельсин?
Решение. Если Яша взял яблоко, то по принципу умножения Полина может осуществить свой выбор
способами. Если Яша взял апельсин,
то - способами.
В первом случае у Полины свобода выбора большая.