Презентация на тему Координаты точек на координатной плоскости

отводится 5 часов в 6 классе и 2 часа

в 7 классе. В 6 классе данная тема является «проходной», так как не имеет логического продолжения, что не позволяет ученикам хорошо закрепить полученные знания. В 7 классе это повторение перед изучением темы «Функции», за 2 урока необходимо повторить и закрепить знания по данной теме. Практические задания на построение точек на координатной плоскости занимают много времени, построение точек на школьной доске, зачастую, не является наглядным. Все это не способствует максимально плодотворному изучению темы.
Данная работа позволяет оптимизировать учебный процесс. Презентация состоит из трех частей: объяснение нового материала, закрепление, тренажер. Каждая часть состоит из отдельных тематических слайдов, переход на каждый осуществляется по гиперссылке. Работа на каждом отдельном слайде осуществляется по щелчку мыши, что позволяет организовать работу на уроке в оптимальном для учащихся темпе, при необходимости возвращаться к ранее выполненному действию.
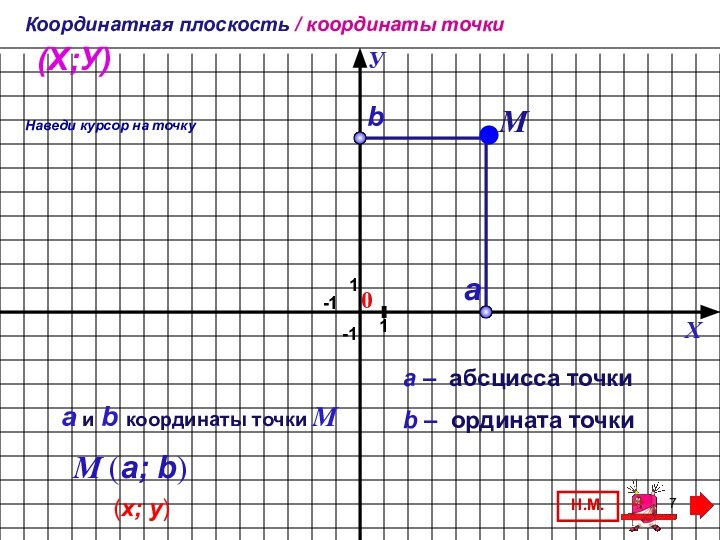
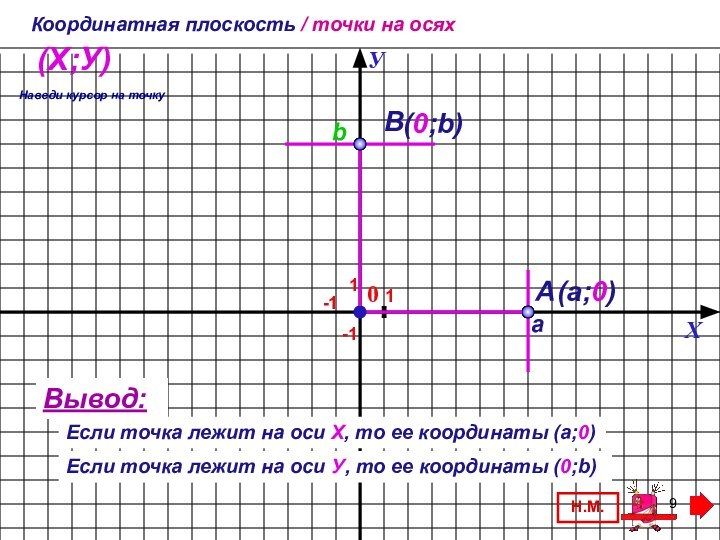
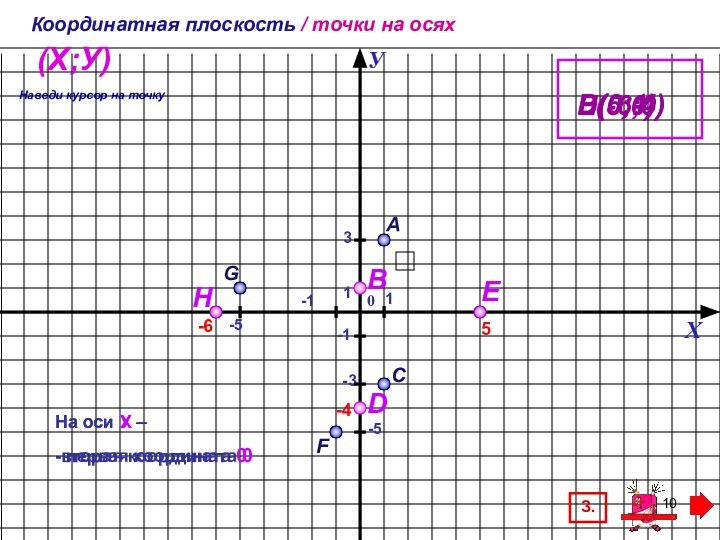
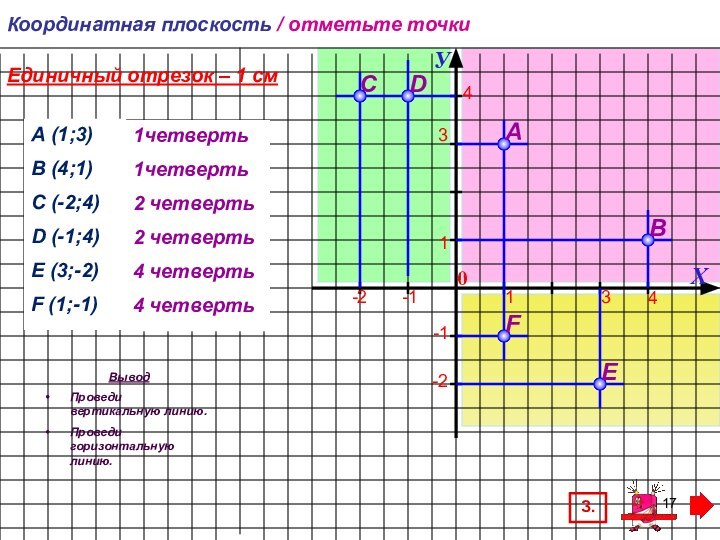
Объяснение нового материала наглядно, доступно, соответствует учебнику, подача материала происходит малыми дозами по щелчку мыши. Можно использовать для фронтальной работы в классе и для самостоятельного изучения.
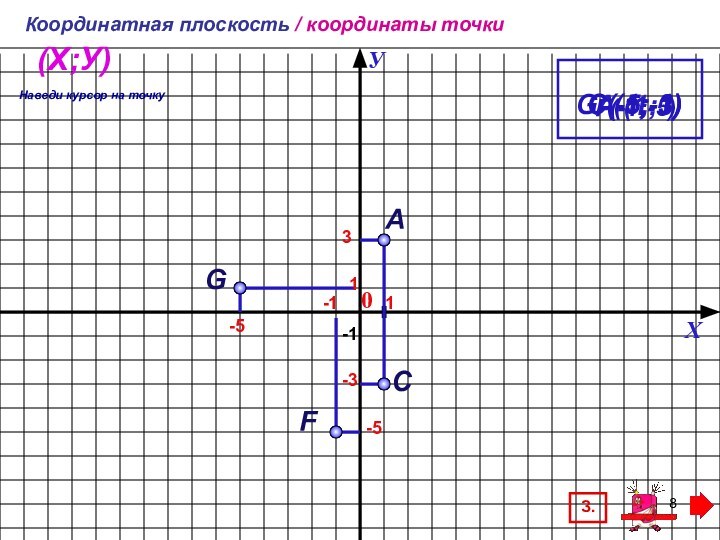
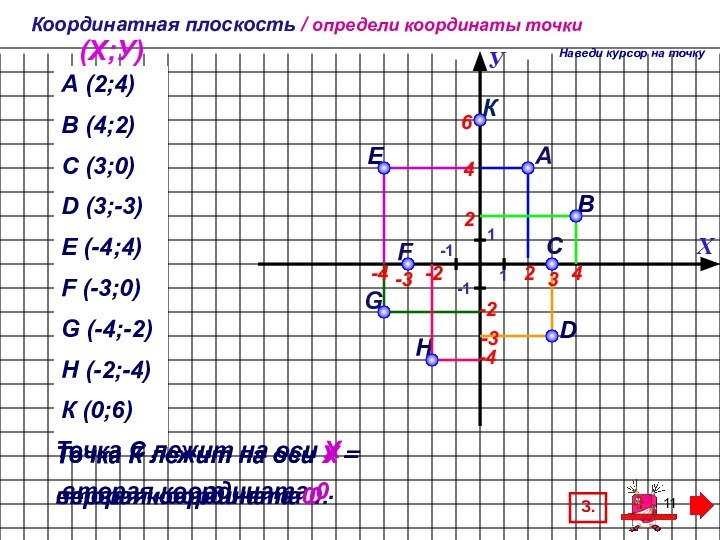
Закрепление – выполнение заданий с пояснениями, комментариями. Наглядно, доступно, соответствует учебнику, подача материала происходит малыми дозами по щелчку мыши. Можно использовать для фронтальной работы в классе и для самостоятельного изучения.
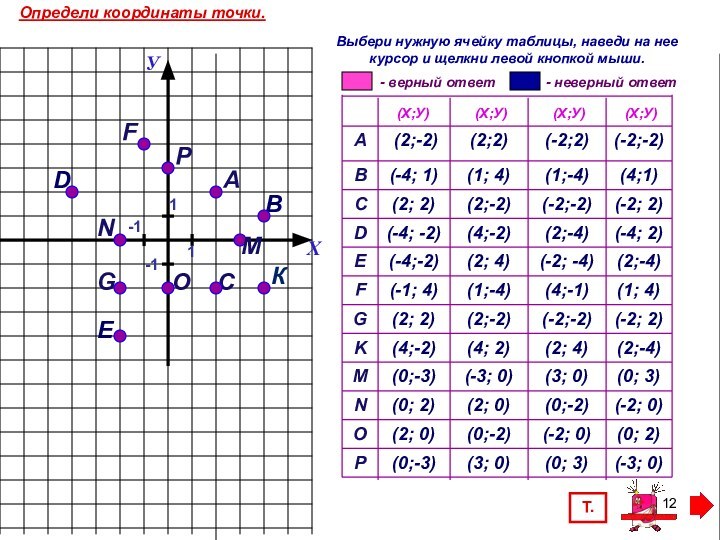
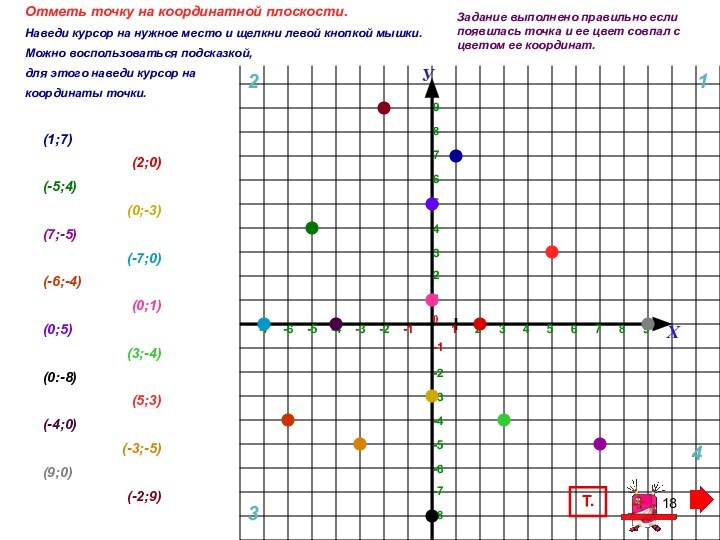
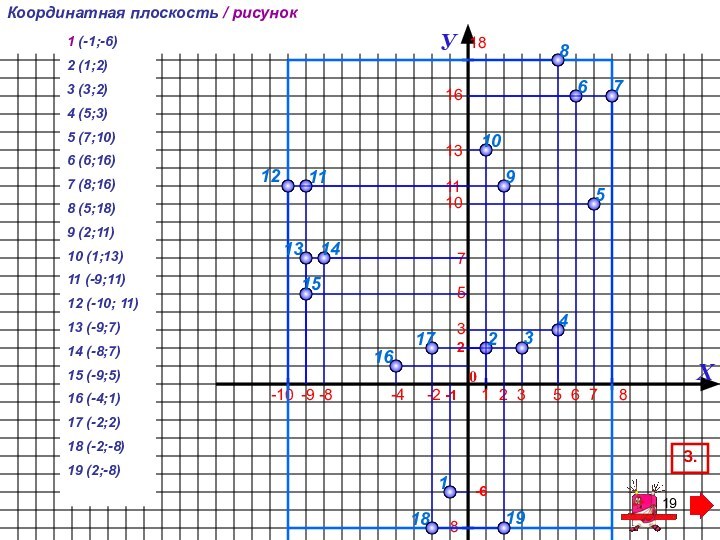
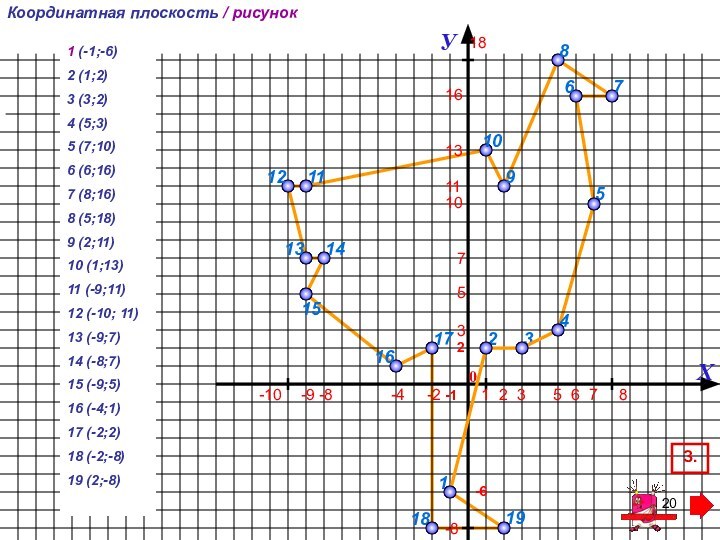
Тренажер выполнен в трех основных типах заданий: определить координаты точки, определить месторасположение точки на координатной плоскости, отметить точку на координатной плоскости. Прост в использовании.

Источники информации.

Историческая справка
Методические рекомендации
Технические рекомендации
Н.М.
З.
Т.
Содержание
И.

осях (границы) (слайд № 9)
Координатные четверти (слайд № 13)
Как

отметить точку (слайд № 16)

Объяснение нового материала

Н.М.

осях (границы) (слайд № 10)
Определи координаты точки (слайд №

11)
Определи в какой четверти точка (слайд № 14)
Как отметить точку (слайд № 17)
Отметь точку (рисунок по координатам) (слайд № 19, 20)

Задания (закрепление теоретического материала)

З.

в какой четверти находится точка (слайд № 15)
Отметь точку

(слайд № 18)
рисунок

Тренажер

Т.

точки М
М (a; b)
(х; у)

а –

абсцисса точки

b – ордината точки

(Х;У)

Н.М.

Наведи курсор на точку

точки
З.






Наведи курсор на точку

лежит на оси Х, то ее координаты (а;0)
Если точка

лежит на оси У, то ее координаты (0;b)

Н.М.

Наведи курсор на точку

У –
- первая координата 0
Н(-6;0)

-6
D(0;-4)
-4
Координатная плоскость / точки

на осях

З.

Наведи курсор на точку

(3;0)
D (3;-3)
Е (-4;4)
F (-3;0)
G (-4;-2)
Н (-2;-4)
К (0;6)
2

4
2
Точка С лежит

на оси Х –
вторая координата 0.

-3

3

4

-3

Точка F лежит на оси Х –
вторая координата 0.

-2

-4

-4

-2

К

Точка К лежит на оси У –
первая координата 0.

6

З.

(Х;У)

Наведи курсор на точку

0)
(0; 2)
N
(0; 3)
(3; 0)
(-3; 0)
(0;-3)
M
(2;-4)
(2; 4)
(4; 2)
(4;-2)
K
(-2; 2)
(-2;-2)
(2;-2)
(2; 2)
G
(1;

4)

(4;-1)

(1;-4)

(-1; 4)

F

(2;-4)

(-2; -4)

(2; 4)

(-4;-2)

E

(-4; 2)

(2;-4)

(4;-2)

(-4; -2)

D

(-2; 2)

(-2;-2)

(2;-2)

(2; 2)

C

(4;1)

(1;-4)

(1; 4)

(-4; 1)

B

(-2;-2)

(-2;2)

(2;2)

(2;-2)

А

N

O

M

P

(Х;У)

(Х;У)

(Х;У)

(Х;У)

Выбери нужную ячейку таблицы, наведи на нее курсор и щелкни левой кнопкой мыши.
- верный ответ - неверный ответ

Определи координаты точки.

Т.

четверть
3 координатная четверть
4 координатная четверть
+
_
_
+
(+;+)

(+;-)
(-;-)
(-;+)


+

_
_
+



Н.М.

четверть
3 четверть
2 четверть
А (-7;5)
В (-5;-7)
С (6;5)
D (2;-4)
Е (-6;9)
F (1;8)
К

( -7;-10)
G (5;-11)
М (0; 5)

2 четверть
3 четверть
1 четверть
4 четверть
2 четверть
1 четверть
3 четверть
4 четверть
?

Определите в какой четверти находится точка.

5

На границе между 1 и 2 четвертями

З.

0; 3)








( -5; 7)








( 9; 0)








( -5; -3)








( 0;

10)

( 7; 4)

( 0; -1)

( -5; 0)

(9; 3)

( 0; -7)

( 5; 0)

( -6; 0)

( 10; -2)

( -7; 3)

( -5; -3)

4 и 1

3 и 4

2 и 3

1 и 2

Граница

4 четверть

3 четверть

2 четверть

1 четверть

Наведите курсор на нужную клетку и сделайте щелчок левой кнопкой мышки.
Можно воспользоваться подсказкой, для этого наведите курсор на ячейки верхней строки таблицы.

Ответ верный

Ответ неверный.

Т.

координата
Х = а
Вторая координата
У = b

а
b
М (а;b)
Отметьте точку
N

(0; c)

Первая координата Х = 0
точка лежит на оси У

Вторая координата

У = c

c

N (0;с)

Отметьте точку
К (d; 0)

Первая координата
Х = d

d

Вторая координата У = 0
точка лежит на оси Х

К (d;0)

Н.М.

Вывод
Проведи вертикальную линию.
Проведи горизонтальную линию.

(-2;4)
D (-1;4)
Е (3;-2)
F (1;-1)

А
3
4

-2
4


D
3
-2

Е
1
1

F
Единичный отрезок – 1

см

1четверть
1четверть
2 четверть
2 четверть
4 четверть
4 четверть

С

В

З.

Вывод
Проведи вертикальную линию.
Проведи горизонтальную линию.

место и щелкни левой кнопкой мышки.
Т.
















Можно воспользоваться подсказкой,
для этого

наведи курсор на
координаты точки.

Задание выполнено правильно если появилась точка и ее цвет совпал с цветом ее координат.

1

3

2

4

(7;10)
6 (6;16)
7 (8;16)
8 (5;18)
9 (2;11)
10 (1;13)
11 (-9;11)
12 (-10; 11)
13

(-9;7)
14 (-8;7)
15 (-9;5)
16 (-4;1)
17 (-2;2)
18 (-2;-8)
19 (2;-8)

-1

-6

1

2

2

3

19

3

5

3

4

7

10

5

16

6

2

6

7

8

11

9

13

10

-9

11

12

7

13

-8

14

5

15

-4

16

-2

17

18

З.

(7;10)
6 (6;16)
7 (8;16)
8 (5;18)
9 (2;11)
10 (1;13)
11 (-9;11)
12 (-10; 11)
13

(-9;7)
14 (-8;7)
15 (-9;5)
16 (-4;1)
17 (-2;2)
18 (-2;-8)
19 (2;-8)

-1

-6

1

2

2

3

19

3

5

3

4

7

10

5

16

6

2

6

7

8

11

9

13

10

-9

11

12

7

13

-8

14

5

15

-4

-2

17

18

16

З.

координаты, по имени великого математика Рене Декарта.

Карл появился на свет в жалком сельском доме в

Брауншвейге, в Германии. Читать научился самостоятельно.
Во всей истории математики нет никого, кто приблизился бы к Гауссу по ранней озарённости. Трёх лет от роду он исправил ошибку в расчётах отца, начислявшего недельный заработок рабочим своей бригады. Впоследствии Гаусс любил вспоминать этот случай и в шутку замечал, что он умел считать раньше, чем научился говорить. Необыкновенные способности вычислять в уме были присущи ему всю жизнь.
После достижения 7 лет Карл пошёл в свою первую сельскую школу. Затем в течение трёх лет обучался в Карловом училище в Брауншвейге, после чего закончил Гёттингенский университет.
День 30 марта 1796 года стал поворотным пунктом в жизни Гаусса. Ему удалось доказать, что можно построить циркулем и линейкой правильный семнадцатиугольник. До этого проблема построения правильных многоугольников оставалась без движения в течение более двух тысячелетий. Считалось, что можно построить квадрат, правильный треугольник, пятиугольник и фигуры, производные от них.
Гаусс один из первых дал связное, последовательное объяснение комплексных чисел и интерпретировал их как точки плоскости.
Гаусс вёл научный дневник, который состоит из 19 небольших страниц и содержит 146 исключительно кратких записей об открытиях или результатах вычислений.
Был дважды женат, имел шестерых детей.
В последние годы жизни страдал от расширения сердца и недостаточности дыхания. Тем не менее он работал, когда мог, хотя у него часто сводило руку.
Умер на 78-ом году жизни.

В детстве Рене не любил учиться, и в семнадцать

лет его увлекали лишь верховая езда и фехтование.
И вдруг всё изменилось. Он снимает себе тихий домик в предместье Парижа и на два года приговаривает себя к изучению математики. "10 ноября 1619 года, - пишет он в своём дневнике, - я начал понимать основания чудесного открытия". Речь идёт об основах аналитической геометрии - нового, рождённого им, раздела математики.
Декарт ввёл и понятие переменной величины, которую Ф.Энгельс назвал "поворотным пунктом в математике".
После долгих скитаний по Европе, Декарт останавливается в Голландии, где живёт 20 лет. Здесь и создаёт он свои знаменитые книги "Рассуждение о методе", "Геометрия", "Метафизические размышления о первой философии", "Начала философии". В Голландии Декарт кроме математики занимается медициной, астрономией, оптикой.
Скончался Декарт 11 февраля 1650 года от воспаления лёгких, не дожив до 54 лет.

Декартовы координаты.

Философия Декарта.

Узнай больше!

Биография, достижения.

координатная плоскость

математик, физик и философ. Родился в Клермоне. В 1631

году с семьёй переезжает в Париж. Жизнь этого француза - одна из самых ярких и трагических биографий в истории естествознания.
В раннем детстве его поразила непонятная нервная болезнь. В 4 года Блез лишился матери и был, по существу, представлен самому себе в выборе игр и занятий.
Отец много занимался с сыном математикой, хотел развить в нём ум, а не память: никогда не заставлял его ничего заучивать наизусть.
В 16 лет Паскаль доказал теорему: "Во всяком шестивершиннике, вписанном в кривую второго порядка, три точки пересечения противоположных сторон лежат на одной прямой", написал трактат о конических сечениях. В 18 лет изобрёл счётную машину - "бабушку" современных арифмометров.
Ряд своих работ Паскаль посвятил арифметическим рядам и биномиальным коэффициентам. В трактате об арифметическом треугольнике он представил таблицу, в которой коэффициенты разложения (a + b)n для разных n расположены в виде треугольника (треугольник Паскаля). Есть все основания утверждать, что Паскаль и Ферма (с которым он переписывался) - основатели новой области математики - теории вероятностей. Большой вклад Паскаль внёс в разработку исчисления бесконечно малых.
Широко известны и его литературные произведения: "Размышления" и "Письма провинциала".
В 24 года Паскаля разбил паралич. Он с трудом передвигался на костылях, его мучила хроническая бессонница. Потом здоровье пошло на поправку, но его постигает новое несчастье: лошади понесли карету, в которой ехал Паскаль, и на мосту через Сену две передние лошади рухнули в воду. Когда к нему подбежали,
Паскаль был без сознания. С этого мгновения можно считать, что он умер, хотя и прожил ещё восемь лет. Умер Блез Паскаль 19 августа 1662 года в возрасте 39 лет.

основные законы механики, открыл законы белого цвета, разработал дифференциальное

и интегральное исчисление.
Он родился вьюжной зимой 1643 года в Вулстропе (Англия). Родился до срока, таким хилым и слабым, что священник считал, что он не жилец на этом свете. Но странно, он не только выжил, но за свою долгую жизнь никогда не болел, к 84 годам потерял лишь один зуб.
Исаак окончил сельскую школу, а потом Королевскую школу в Грэнтэм.
Учился в Кембридже и как-то незаметно превратился из провинциального школьника в совершенно самостоятельного и оригинального исследователя. Потом, спасаясь от чумы, Ньютон уезжает на два года в родную деревушку, где работает сверх всякой меры.
Он уже знает, какие силы держат на небе Луну, но мир узнал об этом только через 20 лет; в характере учёного есть одна странность - он не любит публиковать свои работы.
Независимо от Лейбница разработал основы дифференциального и интегрального исчисления.
Всем школьникам известна формула под названием "Бином Ньютона".
Болезненно самолюбивый, обидчивый и властный, богатый и знаменитый, он был большим спорщиком. Он вступал в споры с Лейбницем, Гуком и другими учёными.
С раздражением пишет он слова: "Я убедился, что, либо не следует сообщать ничего нового, либо придётся тратить все силы на защиту своего открытия".
Ньютон умер в Кенсингтоне, под Лондоном, 31 марта 1727 года от каменной болезни. Незадолго до смерти Исаак Ньютон сказал: "Не знаю, чем я могу казаться миру, но сам себе я кажусь только мальчиком, играющим на морском берегу, развлекающимся тем, что от поры до времени отыскиваю камешек более цветистый, чем обыкновенный, или красную раковину, в то время как великий океан истины расстилается передо мною неисследованным".

мы считаем его русским учёным. Эйлер подарил России самые

значительные свои труды, более тридцати лет прожил в Петербурге.
Приехал в Россию по приглашению царицы Екатерины I. В 1733 году женился в Петербурге. Был отцом 13 детей и дедом 38 внуков.
В Петербурге Эйлер стал адъюнкт-профессором математики, а потом и академиком Петербургской Академии Наук. Работал он широко, с азартом. Стиль Эйлера отличался от многих великих математиков удивительным даром обобщения, осмысления и применения уже открытого.
Эйлер - автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, математической физике и других разделов физики и математики.
Формы его работы антично совершенны, многие математические размышления Эйлера нетронутыми перешли в учебники наших дней.
В трудах Леонардо Эйлера тригонометрия получила современный вид. Он разработал её как науку о тригонометрических функциях, рассматриваемых как отношения соответствующих тригонометрических линий к радиусу. Это позволило понимать под аргументом тригонометрических функций как углы, дуги, так и отвлечённые числа. Впервые в его работах встречаются записи sin х, tg х и другие современные обозначения, в том числе и строчные буквы a, b, c для сторон треугольника и прописные буквы A, B, C - для противоположных углов.
Не вытерпев самоуправства Бирона - фаворита императрицы Анны Ивановны, Эйлер вынужден был уехать в Берлин. Но русская Академия продолжала считать его своим членом. За опубликованные сочинения ему посылали в Берлин деньги, поддерживая материально нуждавшегося учёного.
В 1766 году Эйлер вернулся в Петербург. Вскоре после возвращения начались напасти: Эйлер ослеп. Через пять лет дотла сгорел его дом в Петербурге, только чудом удалось спасти его рукописи. Слепой он много работал, побеждая мрак феноменальной памятью и воображением.
В последний период им подготовлено около 400 работ.
7 сентября 1783 года пил чай, играл с внуком, но вдруг выронил трубку и крикнул: "Умираю!".
В печати появилась крылатая фраза "Эйлер перестал жить и вычислять".
Похоронен Леонард Эйлер в Петербурге.

координатная плоскость

историком, юристом, философом, педагогом, путешественником, дипломатом.
Отличаясь железным здоровьем,

он целыми днями просиживал в отцовской библиотеке. Без разбора читал Платона, Аристотеля, Цицерона, Декарта. Уже в 15 лет Готфрид - студент университета. В 17 лет в поисках серьёзного наставника по математике он переезжает в Иену. Здесь берёт уроки истории, археологии, юриспруденции. Потом возвращается в университет в Лейпциг и в 20 лет пишет первую научную работу по математике "Рассуждение о комбинаторном методе".
В 26 лет Лейбниц в Париже. Здесь начинается наиболее плодотворный период его занятий математикой.
Во время поездки в Лондон он знакомится с Ньютоном. Через 11лет Лейбниц опубликовал свой труд по дифференциальному исчислению.
Много сделал он в математике: ввёл термин "функция", "координаты", "алгоритм"; предвосхитил принципы современной математической логики ("Об искусстве комбинаторики"); создал знаки дифференциала и интеграла; додумался до двоичной системы изображения чисел - азбуки современной вычислительной техники.
Много Лейбниц странствовал по Европе, встречался с русским царём Петром 1. Можно считать, что своей перепиской с русским царём Лейбниц повлиял на формирование Российской Академии наук.
Жестокая подагра останавливает Лейбница от бесконечных путешествий и в Ганиовере приковывает его к креслу. Боль в ногах делается совсем уже невыносимой. Однажды Готфрид принимает "верное снадобье" и через час умирает.

координатная плоскость

математик Н.И. Лобачевский родился в Нижнем Новгороде. Когда Николаю

было 7 лет, его мать с тремя маленькими сыновьями переехала в Казань. В 1802 году Лобачевский был принят в Казанскую гимназию на казённое содержание. Его успехи в математике и в древних языках были феноменальными.
В 1807 году он стал студентом Казанского университета. В 1811 году Лобачевский получил звание магистра и был оставлен при университете для подготовки к профессорскому званию. В 1814 году он получил звание адъюнкта чистой математики и начал читать лекции студентам по теории чисел, а с 1816 года начинает профессорскую деятельность.
С 1827 года по 1846 год Лобачевский - ректор Казанского университета.
День 23 февраля 1826 года стал днём рождения неевклидовой геометрии. На собрании физико-математического факультета Лобачевский изложил математическую работу "Сокращённое изложение начал геометрии". Говоря о пятом постулате Евклида, Лобачевский отметил, что строго доказать его нельзя, а известные доказательства являются только объяснениями, и подкрепил свой вывод созданием геометрии, основанной на гипотезе острого угла, в которой имеется не одна прямая, параллельная данной прямой и проходящая через данную точку, а две. Ни одна из этих двух параллельных прямых Лобачевского не пересекается с прямой, которой они обе параллельны, так же как и любая прямая, лежащая внутри угла, образованного двумя указанными параллельными прямыми, и проходящая через фиксированную точку. Эта ситуация, кажущаяся странной, "реализуется" на псевдосфере. Для повседневных целей различие между геометриями Евклида и Лобачевского слишком мало, но каждая из них совместна сама по себе и каждая адекватна человеческому опыту.
Геометрия Лобачевского была первой из нескольких, построенных его последователями.
В последние годы жизни здоровье Лобачевского сильно пошатнулось, быстро ухудшалось зрение. Последнюю свою работу "Пангеометрия" он уже диктовал, а не писал собственной рукой.
Умер Н.И. Лобачевский 62 лет от роду.

координатная плоскость

№ 92, Красноярск
Должность: учитель

математики
Стаж работы: 18 лет
Категория: высшая
Образование: высшее, КГПИ 1989 г.

1 слайд

7» (УМК А.Г.Мордкович)
Методические пособия для учителя к учебникам «Математика

6», «Алгебра 7» (УМК А.Г.Мордкович).
Интернет

2
Вариант № 3
Вариант № 4