- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Круг и окружность
Содержание









Слайд 3 Где используются круги
Круги используются в колёсах машин, велосипедов. Ещё круги используются в спорте, в быту.
На первый взгляд, кажется, что круг - очень обычная и простая фигура, но это далеко не так. На самом деле окружность и круг таят в себе множество загадок и тайн, имеют увлекательную историю их изучения. Математики стали активно заниматься изучением этих геометрических фигур очень давно.
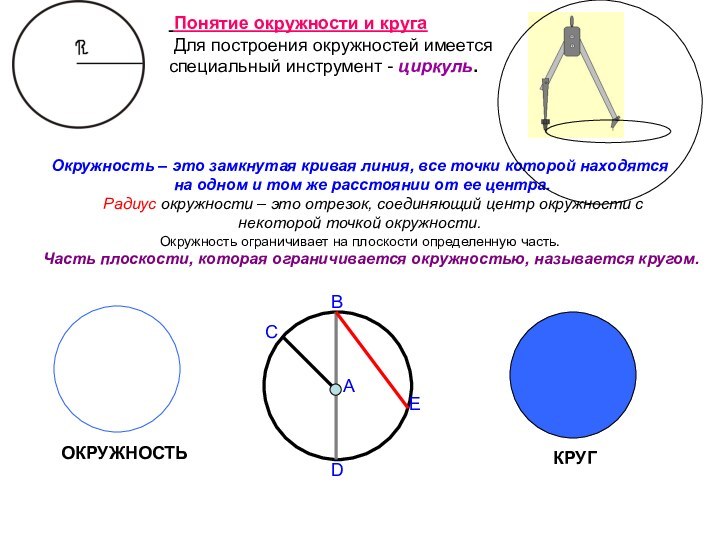
Слайд 4 Окружность – это замкнутая кривая линия, все точки
которой находятся на одном и том же расстоянии от
ее центра. Радиус окружности – это отрезок, соединяющий центр окружности с некоторой точкой окружности. Окружность ограничивает на плоскости определенную часть. Часть плоскости, которая ограничивается окружностью, называется кругом.ОКРУЖНОСТЬ
КРУГ
Понятие окружности и круга
Для построения окружностей имеется специальный инструмент - циркуль.
А
В
E
D
С
Слайд 5
Длина окружности
Если «опоясать» стакан ниткой, а потом распрямить её, то длина нитки будет приближённо равна длине нарисованной окружности.
Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость. Чтобы убедиться в этом, я проделал следующий опыт.
С=84см
d=8см
π≈3,141…
С=32,7см
d=10,5см
π≈3,1142857…
Взял несколько кругов, измерил непосредственным способом их окружности и
диаметры, а затем нашёл отношения длины каждой окружности к своему
диаметру. Я получил одно и то же значение этого отношения, близкое к числу
3,1.
Слайд 6 Таким образом, для вычисления длины окружности была установлена
известная
вам формула С = 2πR
Подсчёты показали, что с точностью
до десятитысячных получается 3,1415…. Если значение округлить до сотых, то получим значение 3,14. Примерно такую же точность даёт значение дроби 22/7Площадь круга
S = πR²
Зависимость площади круга от длины его радиуса
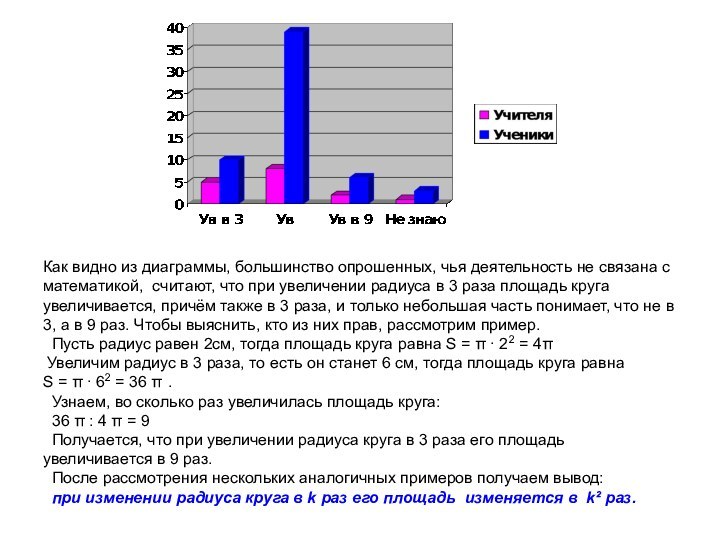
При проведении социологического опроса был задан вопрос: «Что произойдёт с площадью круга, если его радиус увеличится в 3 раза?»
Данные, полученные при ответе на этот вопрос, представлены в диаграмме.
Слайд 7 Как видно из диаграммы, большинство опрошенных, чья деятельность
не связана с математикой, считают, что при увеличении радиуса
в 3 раза площадь круга увеличивается, причём также в 3 раза, и только небольшая часть понимает, что не в 3, а в 9 раз. Чтобы выяснить, кто из них прав, рассмотрим пример. Пусть радиус равен 2см, тогда площадь круга равна S = π ∙ 22 = 4π Увеличим радиус в 3 раза, то есть он станет 6 см, тогда площадь круга равна S = π ∙ 62 = 36 π . Узнаем, во сколько раз увеличилась площадь круга: 36 π : 4 π = 9 Получается, что при увеличении радиуса круга в 3 раза его площадь увеличивается в 9 раз. После рассмотрения нескольких аналогичных примеров получаем вывод: при изменении радиуса круга в k раз его площадь изменяется в k² раз.
Слайд 8
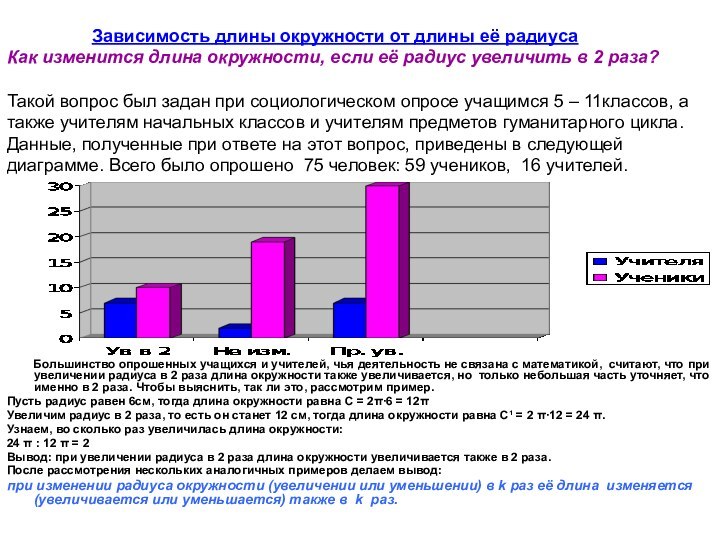
Большинство опрошенных учащихся и
учителей, чья деятельность не связана с математикой, считают, что
при увеличении радиуса в 2 раза длина окружности также увеличивается, но только небольшая часть уточняет, что именно в 2 раза. Чтобы выяснить, так ли это, рассмотрим пример.Пусть радиус равен 6см, тогда длина окружности равна С = 2π∙6 = 12π
Увеличим радиус в 2 раза, то есть он станет 12 см, тогда длина окружности равна С¹ = 2 π∙12 = 24 π.
Узнаем, во сколько раз увеличилась длина окружности:
24 π : 12 π = 2
Вывод: при увеличении радиуса в 2 раза длина окружности увеличивается также в 2 раза.
После рассмотрения нескольких аналогичных примеров делаем вывод:
при изменении радиуса окружности (увеличении или уменьшении) в k раз её длина изменяется (увеличивается или уменьшается) также в k раз.
Зависимость длины окружности от длины её радиуса
Как изменится длина окружности, если её радиус увеличить в 2 раза?
Такой вопрос был задан при социологическом опросе учащимся 5 – 11классов, а также учителям начальных классов и учителям предметов гуманитарного цикла.
Данные, полученные при ответе на этот вопрос, приведены в следующей диаграмме. Всего было опрошено 75 человек: 59 учеников, 16 учителей.
Слайд 9
Число ПИ В наше время с помощью ЭВМ число π вычислено с миллионами правильных знаков после запятой. Но такая точность не нужна ни в каких вычислениях и представляет скорее технический, чем научный интерес. Число π присутствует в чертежах и вычислениях, выполняемых электронными машинами при подготовке и проведении полетов в космос; оно представляет необходимое количество своих десятичных знаков всякий раз, когда они нужны инженерам, рассчитывающим цилиндрические, сферические или конические части машин, физикам и астрономам, когда они проводят приближенные вычисления по формулам, в которых среди фундаментальных постоянных появляется и π. В клинописных табличках Древнего Междуречья содержится запись о том, что длина окружности в 3 раза больше диаметра. Однако уже во 2 тысячелетии до н.э. математики Древнего Египта находили более точное отношение. По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3 10/71 и 3 1/7.
Слайд 10
Круги в архитектуре
Окружность как совершенная геометрическая форма всегда привлекала внимание художников, архитекторов.
Слайд 11
Заключение
Предметы круглой формы часто встречаются в окружающей нас жизни, поэтому всё, что связано с кругом и окружностью, имеет большую практическую направленность. Следовательно, результаты моей работы могут быть полезны в практической деятельности человека.





























