Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Лабиринтики и quickunion

Содержание

ПРОСЫПАЕМСЯ!!!Сколько связанных компонент можно получить при выполнении следующей последовательности команд union на наборе из 10 элементов?1-2; 3-4; 5-6; 7-8; 7-9; 2-8; 0-5; 1-9Варианты:
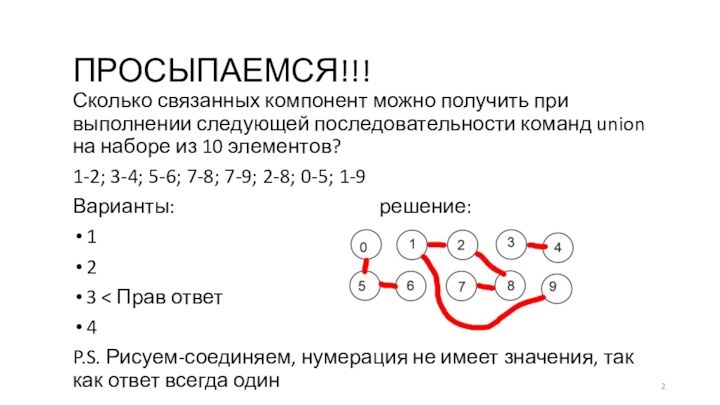
Лабиринтики и quickunion ПРОСЫПАЕМСЯ!!!Сколько связанных компонент можно получить при выполнении следующей последовательности команд union на ПРОСЫПАЕМСЯ!!!Какое максимальное число элементов массива id[] может быть изменено при выполнении одной ПРОСЫПАЕМСЯ!!!Есть структура данных quick-union из 10 элементов и их id[] соответственно равны 0 ПРОСЫПАЕМСЯ!!!Каким может быть максимальное число запросов к массиву во время операции поиска ПРОСЫПАЕМСЯ!!!Дан массив id[] для WQU алгоритмаКакой id[] изменится при выполнении операции Union(3,6)Варианты:ID[0]ID[3]ID[6]ID[8] < см. сл слайд0156273849 ОтветОтвет – id[8]. Так как сравниваем алгоритмы по числу элементов, а не Вопрос для суперигрыКогда открывается новый узел, сколько раз вызывается команда UNION()?Варианты:0,1,2,3 или Анализ алгоритмов ПРОСЫПАЕМСЯ!Дано: N = 1,000,000 (1 миллион)Во сколько быстрее работает алгоритм N*log2N по ПросыпаемсяВы измеряете время работы программы T(N) (сек), как функции размера входных данных Просыпаемся!Сколько обращений к массиву происходит в следующем фрагменте кода? ОтветНе все тройные циклы работают за кубическое время. В данном случае в Просыпаемся!Чему равно максимальное число обращений к массиву в алгоритме бинарного поиска в Просыпаемся!Какая из следующих функций O(N3)? ОтветO() определяет верхнюю границу роста функции, кубичность характерна для них всех. Просыпаемся!Сколько памяти (в байтах) использует взвешенный QuickUnionUF состоящий из массива в N Стеки и очереди Просыпаемся!Какой из следующих входных данных в стек не сможет воспроизвести следующий вывод Просыпаемся!Дана ссылка first, ссылающаяся на 1ый элемент стека (реализация с пом списка ОтветX.next.next != null – проверяет, не является ли следующий за ним элемент Просыпаемся!Предположим, что начиная с пустой структуры, мы производим N push() операций в Сортировка ПРОСЫПАЕМСЯ!Число сравнений для уже отсортированного входного массива алгоритма сортировки с выбором…ЛинейноКвадратично < ПросыпаемсяЧисло сравнений для уже отсортированного массива для метода сортировки с вставкой…ПостоянноЛогарифмичноЛинейно < ПРОСЫПАЕМСЯ!Число сравнений для уже отсортированного массива для метода сортировки Шелла при инкременте Просыпаемся!Каково максимальное число раздач 52 карт? 52! На предыдущем слайде ответ Просыпаемся!Максимальное число вершин на выпуклой оболочке для множества из N точек…ПостоянноЛогарифмичноЛинейно <
Слайды презентации

Слайд 2 ПРОСЫПАЕМСЯ!!!
Сколько связанных компонент можно получить при выполнении следующей

ПРОСЫПАЕМСЯ!!!Сколько связанных компонент можно получить при выполнении следующей последовательности команд union

последовательности команд union на наборе из 10 элементов?
1-2; 3-4;

5-6; 7-8; 7-9; 2-8; 0-5; 1-9
Варианты: решение:
1
2
3 < Прав ответ
4
P.S. Рисуем-соединяем, нумерация не имеет значения, так как ответ всегда один

Слайд 3 ПРОСЫПАЕМСЯ!!!
Какое максимальное число элементов массива id[] может быть

ПРОСЫПАЕМСЯ!!!Какое максимальное число элементов массива id[] может быть изменено при выполнении

изменено при выполнении одной команды union когда мы используем

quick-find, а размер массива N?
Варианты:
1
LgN
N-1 < Прав ответ
N

Слайд 4 ПРОСЫПАЕМСЯ!!!
Есть структура данных quick-union из 10 элементов и

ПРОСЫПАЕМСЯ!!!Есть структура данных quick-union из 10 элементов и их id[] соответственно

их id[] соответственно равны
0 9 6 5 4 2

6 1 0 5
Чему равны корни 3 и 7, соответственно?
Варианты:
3 и 7
4 и 4
6 и 4
6 и 6 <Прав ответ

Слайд 5 ПРОСЫПАЕМСЯ!!!
Каким может быть максимальное число запросов к массиву

ПРОСЫПАЕМСЯ!!!Каким может быть максимальное число запросов к массиву во время операции

во время операции поиска (connected) для алгоритма Quick-union от

числа элементов N в массиве
Варианты:
постоянно
логарифмично
Линейно < пр. отв
Квадратично

Операция connected сравнивает корни 2ух чисел,
возможна ситуация, когда числа находятся в самом низу
необходимо пройти весь массив от начала до конца, чтобы
узнать корни

Слайд 6 ПРОСЫПАЕМСЯ!!!
Дан массив id[] для WQU алгоритма


Какой id[] изменится

ПРОСЫПАЕМСЯ!!!Дан массив id[] для WQU алгоритмаКакой id[] изменится при выполнении операции Union(3,6)Варианты:ID[0]ID[3]ID[6]ID[8] < см. сл слайд0156273849

при выполнении операции Union(3,6)
Варианты:
ID[0]
ID[3]
ID[6]
ID[8] < см. сл слайд
0
1
5
6
2
7
3
8
4
9

Слайд 7 Ответ
Ответ – id[8]. Так как сравниваем алгоритмы по

ОтветОтвет – id[8]. Так как сравниваем алгоритмы по числу элементов, а

числу элементов, а не по высоте.
У дерева с 0

вес ~ 6, a у дерева 8 вес ~ 4. По правилу присоединяем меньшее дерево к большему, сравнивая по весу => меняется id[8]

Слайд 8 Вопрос для суперигры
Когда открывается новый узел, сколько раз

Вопрос для суперигрыКогда открывается новый узел, сколько раз вызывается команда UNION()?Варианты:0,1,2,3

вызывается команда UNION()?
Варианты:
0,1,2,3 или 4 < пр. ответ
1,2,3 или

4
2,3 или 4
4

Сначала проверяем состояние соседей
(открыты или закрыты). С открытыми
Делаем команду union, с закрытыми
– ничего не делаем. Поэтому вызовов
Union может быть от 0 до 4

Слайд 9 Анализ алгоритмов

Анализ алгоритмов

Слайд 10 ПРОСЫПАЕМСЯ!
Дано: N = 1,000,000 (1 миллион)
Во сколько быстрее

ПРОСЫПАЕМСЯ!Дано: N = 1,000,000 (1 миллион)Во сколько быстрее работает алгоритм N*log2N

работает алгоритм N*log2N по сравнению с N2?
в 20
в 1000
в

50,000 < пр отв
в 1,000,000

Слайд 11 Просыпаемся
Вы измеряете время работы программы T(N) (сек), как

ПросыпаемсяВы измеряете время работы программы T(N) (сек), как функции размера входных

функции размера входных данных N. Какая из этих функций

лучше всего описывает время работы.

3.3 * 10-4 * N
N2
5.0 * 10-9 * N2 < Пр отв.
6.25 * 10-9 * N2

Подставляем самый большой N
В каждую из функций и считаем T
Там где он будет точнее, та и функция

Слайд 12 Просыпаемся!
Сколько обращений к массиву происходит в следующем фрагменте

Просыпаемся!Сколько обращений к массиву происходит в следующем фрагменте кода?

кода?


Слайд 13 Ответ
Не все тройные циклы работают за кубическое время.

ОтветНе все тройные циклы работают за кубическое время. В данном случае

В данном случае в цикл с параметром k работает

3lgN раз, вместо N раз, так как каждую итерацию k увеличивается вдвое.
Первые 2 цикла работают по N раз каждый
Итого 3/2 * N * N * lgN

Слайд 14 Просыпаемся!
Чему равно максимальное число обращений к массиву в

Просыпаемся!Чему равно максимальное число обращений к массиву в алгоритме бинарного поиска

алгоритме бинарного поиска в отсортированном массиве длины N

Постоянно
Логарифмично

отв.
Линейно
N log N (Linearithmic)

Каждый раз область поиска
(обрабатываемый массив)
Уменьшается в 2 раза при
нахождении середины.
А это подобно логарифму по основанию 2

Слайд 15 Просыпаемся!
Какая из следующих функций O(N3)?


Просыпаемся!Какая из следующих функций O(N3)?

Слайд 16 Ответ
O() определяет верхнюю границу роста функции, кубичность характерна

ОтветO() определяет верхнюю границу роста функции, кубичность характерна для них всех.

для них всех.

Слайд 17 Просыпаемся!
Сколько памяти (в байтах) использует взвешенный QuickUnionUF состоящий

Просыпаемся!Сколько памяти (в байтах) использует взвешенный QuickUnionUF состоящий из массива в

из массива в N элементов?







Hint: 2 integer arrays size

of N

Вещественное число (int) занимает в памяти 4 байта
Если массив состоит из N веществ чисел,
то занимает 4*N байт памяти
В QuickUnion находится 2 целочисленных массива
значит он занимает ~ 8N байт

Слайд 18 Стеки и очереди

Стеки и очереди

Слайд 19 Просыпаемся!
Какой из следующих входных данных в стек не

Просыпаемся!Какой из следующих входных данных в стек не сможет воспроизвести следующий

сможет воспроизвести следующий вывод на экран:
5 4 3 2

1
Варианты:
1 2 3 4 5 - - - - -
1 2 5 - 3 4 - - - -
5 - 1 2 3 -4 - - - < ответ
5 - 4 - 3 - 2-1

Он возвращает: 5 3 4 2 1
Почему? – смотри предыдущие слайды лекции про
стеки

Слайд 20 Просыпаемся!
Дана ссылка first, ссылающаяся на 1ый элемент стека

Просыпаемся!Дана ссылка first, ссылающаяся на 1ый элемент стека (реализация с пом

(реализация с пом списка связанных элементов), в котором минимум

2 элемента, что делает представленный код?



Удаляет первый элемент в стеке
Удаляет второй элемент стека
Удаляет предпоследний элемент стека
Удаляет последний элемент в стеке < пр отв

Слайд 21 Ответ
X.next.next != null – проверяет, не является ли

ОтветX.next.next != null – проверяет, не является ли следующий за ним

следующий за ним элемент последним в стеке. Так как

если a.next == null, то он последний, так как уже ни на что не указывает. Соответственно, как только предпоследний элемент достигается по проходу цикла, условие в while уже не выполняется и происходит выход из цикла. После которого следующий за предпоследним элемент, то есть последний, удаляется (зануляется).

Слайд 22 Просыпаемся!
Предположим, что начиная с пустой структуры, мы производим

Просыпаемся!Предположим, что начиная с пустой структуры, мы производим N push() операций

N push() операций в стеке, реализованном на основе массива

изменяемого размера. Как будет вызываться метод resize()?
Постоянно
Логарифмично < пр. отв
Линейно
Квадратично

Как обычно имеем степень двойки, то есть
Массив каждый раз увеличивается в 2 раза
1 2 4 8 16 32 и тд пока не дойдем до N
Типа.. Массив растет от 1 до N каждый раз
увеличиваясь в 2 раза

Слайд 23 Сортировка

Сортировка

Слайд 24 ПРОСЫПАЕМСЯ!
Число сравнений для уже отсортированного входного массива алгоритма

ПРОСЫПАЕМСЯ!Число сравнений для уже отсортированного входного массива алгоритма сортировки с выбором…ЛинейноКвадратично

сортировки с выбором…
Линейно
Квадратично < ответ на предыдущем слайде (сортировка

#22)
Логарифмично
Экспоненциально

Слайд 25 Просыпаемся
Число сравнений для уже отсортированного массива для метода

ПросыпаемсяЧисло сравнений для уже отсортированного массива для метода сортировки с вставкой…ПостоянноЛогарифмичноЛинейно

сортировки с вставкой…
Постоянно
Логарифмично
Линейно < просто сравниваем соседствующие элемены, левый

эл-т всегда будет меньше правого, условие всегда будет выполняться, следовательно пройдет всего N сравнений
Квадратично

Слайд 26 ПРОСЫПАЕМСЯ!
Число сравнений для уже отсортированного массива для метода

ПРОСЫПАЕМСЯ!Число сравнений для уже отсортированного массива для метода сортировки Шелла при

сортировки Шелла при инкременте 3x+1…
Постоянно
Логарифмично
Линейно
N*logN < на слайде 48

ответ

Слайд 27 Просыпаемся!
Каково максимальное число раздач 52 карт?
52! На

Просыпаемся!Каково максимальное число раздач 52 карт? 52! На предыдущем слайде ответ

предыдущем слайде ответ

  • Имя файла: labirintiki-i-quickunion.pptx
  • Количество просмотров: 87
  • Количество скачиваний: 0
- Предыдущая Экологические проблемы мира
Следующая - День рождения

Похожие презентации

Задачи на движение 5 класс Задачи на движение 5 класс 125
Математика. Призентация. Сағат. минут Математика. Призентация. Сағат. минут 172
Урок математики 2 класс презентация к уроку по математике Урок математики 2 класс презентация к уроку по математике 110
Конспект урока и презентация к уроку математики во 2 классе по теме Проверка вычитания и сложения план-конспект урока по математике (2 класс) Конспект урока и презентация к уроку математики во 2 классе по теме Проверка вычитания и сложения план-конспект урока по математике (2 класс) 107
Числовые и буквенные выражения Числовые и буквенные выражения 143
Возведение в квадрат суммы и разности двух выражений Возведение в квадрат суммы и разности двух выражений 105
Презентация к уроку математики :Нумерация трёхзначных чисел Тест презентация к уроку по математике (2 класс) Презентация к уроку математики :Нумерация трёхзначных чисел Тест презентация к уроку по математике (2 класс) 109
Первый признак равенства треугольников Первый признак равенства треугольников 94
Деление (5 класс) Деление (5 класс) 141
Модуль числа Модуль числа 109
Наибольшее и наименьшее значения функции на отрезке Наибольшее и наименьшее значения функции на отрезке 116
Методическая разработка урока по ФЭМП с логическими кубиками Дьенеша. Мальвина и Буратино методическая разработка по математике (старшая группа) Методическая разработка урока по ФЭМП с логическими кубиками Дьенеша. Мальвина и Буратино методическая разработка по математике (старшая группа) 134
В лабиринте тригонометрических формул В лабиринте тригонометрических формул 98
Азбука геометрической резьбы Азбука геометрической резьбы 101
Координатная плоскость Координатная плоскость 95
Микрокалькулятор Микрокалькулятор 107
Дидактическая игра Кто где? презентация к уроку по математике (средняя группа) Дидактическая игра Кто где? презентация к уроку по математике (средняя группа) 138
Арифметические пятиминутки Арифметические пятиминутки 93
Урок математики в 1 классе : Числа от 0 до 20 презентация урока для интерактивной доски по математике (1 класс) по теме Урок математики в 1 классе : Числа от 0 до 20 презентация урока для интерактивной доски по математике (1 класс) по теме 119
Презентация по математике Расшифруй название сказки Презентация по математике Расшифруй название сказки 33
Презентация Требования к учебному заданию в свете ФГОС Презентация Требования к учебному заданию в свете ФГОС 111
Выделение дробей с одинаковым числителем Выделение дробей с одинаковым числителем 95
Преобразование алгебраических выражений Преобразование алгебраических выражений 125
ДЕЦИМЕТР ДЕЦИМЕТР 98
Как выполняли арифметические действия в Древнем Риме? Как выполняли арифметические действия в Древнем Риме? 118
Урок математики в 5 классе Урок математики в 5 классе 125
Действия с величинами Действия с величинами 111
Обыкновенные дроби Обыкновенные дроби 161
Веселый счет презентация к занятию по математике (старшая группа) Веселый счет презентация к занятию по математике (старшая группа) 97
презентация к уроку математики по теме Нумерация чисел от 0 до 10 презентация к уроку по математике (1 класс) презентация к уроку математики по теме Нумерация чисел от 0 до 10 презентация к уроку по математике (1 класс) 108