- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Лабораторный практикум по решению некоторых задач математики
Содержание
- 2. Численные вычисленияАрифметикаВычисление значений математических функцийСимвольные вычисленияПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙПреобразование многочленовПреобразование рациональных выраженийКомплексные числаПреобразования тригонометрических выраженийРЕШЕНИЕ УРАВНЕНИЙ СОДЕРЖАНИЕ
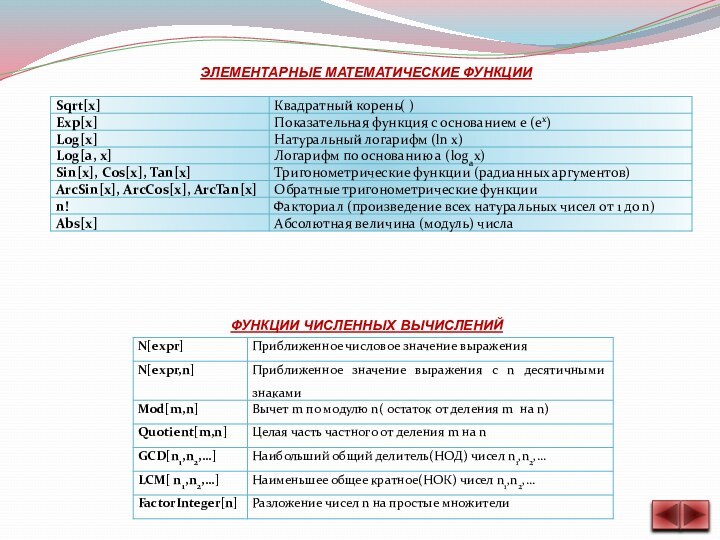
- 3. ЭЛЕМЕНТАРНЫЕ МАТЕМАТИЧЕСКИЕ ФУНКЦИИФУНКЦИИ ЧИСЛЕННЫХ ВЫЧИСЛЕНИЙ
- 4. С помощью Математики можно проводить арифметические вычисления
- 5. С помощью функции Mod вычислен остаток от
- 6. Аргументы всех функций в программе Mathematica заключаются
- 7. СТРУКТУРНЫЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИФУНКЦИИ ОПРЕДЕЛЕНИЯ СТРУКТУРЫ МНОГОЧЛЕНААЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
- 8. Даны многочлены p, q , t и
- 9. x2y+x+xy2+y+2xy+26a3-21a2b+2ab2-7b3-y6-y5+y4+y316ab2-10c3+32ac2-5b2cС помощью функции Factor многочлены разложены на множители.Преобразования алгебраических выраженийПреобразование многочленовСОДЕРЖАНИЕ ЗАДАНИЯ
- 10. p=121y2+11xy-66xz-88yz+33y-33zt=36xy3-90y2+36xy+6x+30g=3a3-15a2b+5ab2q=-3x4y2-6x2y2+9x2y4В многочленах p и t за скобки
- 11. q=(2+x-4y)3+(2-z)(1+x+4y)3Многочлен q приведен к стандартному виду.t=10+18x+12x2+3x3-24y+12x2y+192y2+144xy2+64y3-z-3xz-3x2z-x3z-12yz-24xyz-12x2yz-48y2z-48xy2z-64y2zС помощью
- 12. f=x6+2yx4-4x3-3x2+8x-5g=x3+x2-x+1Введены многочлены f и g.Используя функцию PolynomialQuotient
- 13. ФУНКЦИИ ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ВЫРАЖЕНИЯМИПусть P= P(x,y,…,z)- рациональное выражение.
- 14. Введено рациональное выражение p.Функция ExpandNumerator раскрывает скобки
- 15. Введено рациональное выражение q.С помощью функции Factor
- 16. ОПЕРАЦИИ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
- 17. Извлечение квадратного корня из отрицательного числа
- 18. ОПЕРАЦИИ С ТРИГОНОМЕТРИЧЕСКИМИ ВЫРАЖЕНИЯМИ
- 19. Введено выражение d.С помощью функции TrigExpand d
- 20. ЗНАКИ, ИСПОЛЬЗУЕМЫЕ В УРАВНЕНИЯХ, НЕРАВЕНСТВАХ, ИХ СИСТЕМАХ И СОВОКУПНОСТЯХФУНКЦИИ, ИСПОЛЬЗУЕМЫЕ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ
- 21. Рассмотрим основные функции Математики, предназначенные для решения
- 22. Воспользовавшись функцией Solve также можно решить иррациональное,
- 23. С помощью функции Solve решена система линейных
- 24. СОДЕРЖАНИЕ ЗАДАНИЯ
- 25. СОДЕРЖАНИЕ ЗАДАНИЯ
- 26. СОДЕРЖАНИЕ ЗАДАНИЯ
- 27. Скачать презентацию
- 28. Похожие презентации


























Слайд 2
Численные вычисления
Арифметика
Вычисление значений математических функций
Символьные вычисления
ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
Преобразование
многочленов
Слайд 4 С помощью Математики можно проводить арифметические вычисления подобно
тому, как они делаются на электронном калькуляторе. Необходимо набрать
для ввода 15+113, нажать Shift+Enter, и Математика напечатает результат 128.В отличие от калькулятора, Математика может дать точный результат 915.
Имеющаяся в Математике функция N используется для получения приближенного результата. Знак % ставится вместо выражения введенного в предыдущей входной ячейке. Ответ дается в стандартном математическом виде и содержит 6 знаков (по умолчанию).
Числовой результат можно получить с любой степенью точности. В этом примере 915 вычислено с разрядностью 15 знаков.
Математика может дать результат в виде рационального числа. 8/9+11/13=203/117 .
В примере 956/26 задано точное рациональное число, оно приведено к несократимой дроби, не изменив тип числа.
Численные вычисления
арифметика
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 5 С помощью функции Mod вычислен остаток от деления
317 на 89.
Функция Quotient вычисляет целую часть от деления
315 на 36.GCD[360,195]- найден НОД чисел 360 и 195.
LCM[372,114]- найдено НОК чисел 372 и 114.
С помощью функции FactorInteger число разложено на простые множители.
Численные вычисления
арифметика
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 6 Аргументы всех функций в программе Mathematica заключаются в
квадратные скобки. Наименования встроенных функций в программе Математика начинаются
с заглавных букв.Pi^4//N =97,4091- вычислено приближенное значение
25!=1۠•2•3….•24•25= 15511210043330985984000000
N[%] =0,55112*1025- это приближенное значение предыдущего выражения.
С помощью функций Tan, Sin, ArcCos, ArcSin, Log , Exp вычислены:
Tan[Pi/3] Sin[Pi/4] ArcCos[1/2] ArcSin[-0.65]
Log[3,6561] Exp[2.7]
Здесь Математика без указания функции N дала приближенное значение е 2,7, так как в записи значения аргумента присутствует десятичная точка.
Численные вычисления
Вычисление значений математических функций
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 7
СТРУКТУРНЫЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
ФУНКЦИИ ОПРЕДЕЛЕНИЯ СТРУКТУРЫ МНОГОЧЛЕНА
АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ
НАД МНОГОЧЛЕНАМИ
Слайд 8 Даны многочлены p, q , t и g
.
p= 5a2b+2+4ab2-3a2b-7
q= 2a2x3-ax3-a4-a2x3+ax3+2a4
t= 3a4b2-0.8b4b2-2ab3b+b3b2-1
g= 5x2y2-5x3xy-x2y+6xy2
С помощью функции Expand приведены
подобные члены в многочленах и они представлены в стандартном виде. Тот же самый результат получен после нажатия клавиш Shift+Enter, Математика переставила члены и привела подобные слагаемые, тем самым многочлен принял стандартный вид.Преобразования алгебраических выражений
Преобразование многочленов
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 9
x2y+x+xy2+y+2xy+2
6a3-21a2b+2ab2-7b3
-y6-y5+y4+y3
16ab2-10c3+32ac2-5b2c
С помощью функции Factor многочлены разложены на множители.
Преобразования
алгебраических выражений
Преобразование многочленов
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 10
p=121y2+11xy-66xz-88yz+33y-33z
t=36xy3-90y2+36xy+6x+30
g=3a3-15a2b+5ab2
q=-3x4y2-6x2y2+9x2y4
В многочленах p и t за скобки вынесен
числовой множитель.
В многочленах g и q за скобки вынесены
множители, не зависящие от b, x и y соответственно.Преобразования алгебраических выражений
Преобразование многочленов
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 11
q=(2+x-4y)3+(2-z)(1+x+4y)3
Многочлен q приведен к стандартному виду.
t=10+18x+12x2+3x3-24y+12x2y+192y2+144xy2+64y3-z-3xz-3x2z-x3z-12yz-24xyz-12x2yz-48y2z-48xy2z-64y2z
С помощью функции
PolynomialQ проведен тест: является ли t многочленом от x,y,z?
Ответ: да. (True – истина) .
Применив функции Variables дан список всех переменных многочлена t.
Благодаря функции Length определено число всех членов многочлена t.
С помощью функции Exponent определена наивысшая степень переменного x в многочлене t.
Используя функции Coefficient выписан множитель при xy2 в многочлене t.
Преобразования алгебраических выражений
Преобразование многочленов
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 12
f=x6+2yx4-4x3-3x2+8x-5
g=x3+x2-x+1
Введены многочлены f и g.
Используя функцию PolynomialQuotient найдем
частное от деления f на g.
С помощью функции
PolynomialRemainder найден остаток от деления f на g. p=9x4+5x2+1
q=3x3+2x2+1
Введены многочлены p и q.
С помощью функции PolynomialGCD вычислен наибольший общий делитель многочленов p и q.
Функция PolynomialLCM дает возможность найти наименьшее общее кратное p и q.
Используя функцию Resultant найден результант многочленов p и q.
Преобразования алгебраических выражений
Преобразование многочленов
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 14
Введено рациональное выражение p.
Функция ExpandNumerator раскрывает скобки в
числителях всех дробей.
С помощью функции ExpandDenominator раскрыты
скобки в знаменателях дробей, а в числителях- нет.Функции Expand и Factor также применимы и к рациональным выражениям.
Функция Expand раскрывает скобки в числителях, причем числители почленно поделены на знаменатели и, наконец, функция FullSimplify упрощает выражение полностью.
Преобразования алгебраических выражений
Преобразование рациональных выражений
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 15
Введено рациональное выражение q.
С помощью функции Factor
дроби приведены к общему знаменателю, выполнено сложение дробей, у
полученной дроби разложены на множители числитель и знаменатель и даже произведено сокращение общего множителя в числителе и знаменателе.Функция Together производит действия с дробями, полученная в результате дробь приведена к несократимому виду.
Применив функцию Cancel к выражению q проведено сокращение одной из дробей (где это возможно). Действия с дробями не проводились, разложение на множители произведено только в знаменателе той дроби, которая подвергалась сокращению.
Преобразования алгебраических выражений
Преобразование рациональных выражений
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 17 Извлечение квадратного корня из отрицательного числа дает
чисто мнимое число. В данном примере
Извлечен
квадратный корень из комплексного числа, являющегося точным квадратом: Получено числовое значение логарифмической функции комплексного аргумента.
Получено комплексное число, сопряженное (4-2 i)4
Введен многочлен над полем C.
g=(-1+(x-iy)5)(1+(x+iy)5)
С помощью функции ComplexExpand раскрыты скобки в многочлене g, а с помощью функции Factor многочлен разложен на множители.
Преобразования алгебраических выражений
Комплексные числа
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 19
Введено выражение d.
С помощью функции TrigExpand d преобразовано
в выражение, содержащее только тригонометрические функции от x.
Функция
TrigFactor представляет выражение в виде дроби, числитель и знаменатель которой разложены на линейные относительно тригонометрических функций множители.Используя функцию TrigFactorList получим то же самое, но ответ дан в виде списка множителей, при каждом из которых указывается степень.
С помощью функции TrigReduce выражение свернуто в одночлен, содержащий тригонометрические функции комбинированных аргументов. Используя FullSimplify приводим d к самому простому виду.
Функция TrigToExp выражение sh x + ch x привела к рациональной функции от экспонент.
Применяя функцию ExpToTrig выражение ex переведено в тригонометрическую форму.
Преобразования алгебраических выражений
Преобразования тригонометрических выражений
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 20 ЗНАКИ, ИСПОЛЬЗУЕМЫЕ В УРАВНЕНИЯХ, НЕРАВЕНСТВАХ, ИХ СИСТЕМАХ И
СОВОКУПНОСТЯХ
ФУНКЦИИ, ИСПОЛЬЗУЕМЫЕ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ
Слайд 21 Рассмотрим основные функции Математики, предназначенные для решения уравнений
и их систем.
С помощью функции Solve решено кубическое уравнение
(x+3)3-(x+1)3=56 , его точные корни даны в виде списка правил подстановок. С помощью функции Roots решено тоже самое уравнение, корни даются в виде совокупности простейших уравнений. -рациональное уравнение с параметром. Функция Solve находит решение уравнения с параметром, не рассматривая их специфическое значение, при которых решение существует. Если таковые ожидаются, то лучше использовать функцию Reduce, учитывающую все возможные решения. Также с помощью функции Solve можно решать уравнения, содержащие неизвестную под знаком модуля. Когда Математика не может дать точные выражения для корней уравнения, она дает ответ в таком виде; #1 здесь означает переменное. Из этого ответа следует только то, что рассматриваемое уравнение имеет пять корней над полем комплексных чисел, в таком случае целесообразно применять функцию NSolve для нахождения приближенных значений корней.
В последнем примере найдены приближенные решения уравнения.
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 22 Воспользовавшись функцией Solve также можно решить иррациональное, логарифмическое,
тригонометрическое уравнение.
Функция FindRoot предназначена для вычисления приближенного
значения решения уравнения при заданном начальном приближении к решению.При помощи графической функции Plot построен график функции Sin x- x2
на промежутке [-2;2]. По графику определяем нули функции: x=0 (точное значение) и x≈0,9.
Теперь можно найти приближенное значение одного из корней уравнения по его начальному значению.
СОДЕРЖАНИЕ
ЗАДАНИЯ
Слайд 23
С помощью функции Solve решена система линейных уравнений.
Введена
матрица коэффициентов при неизвестных.
Введен столбец свободных членов.
С помощью функции
LinearSolve получено решение системы. СОДЕРЖАНИЕ
ЗАДАНИЯ





























