- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Коэффициент корреляции τ Кендалла
Содержание
- 2. Коэффициент корреляцииКоэффициент корреляции (тау) Кендалла относиться к
- 3. Коэффициент корреляцииПодсчет коэффициента может осуществляться по трем тождественным формулам. Первая формула:
- 4. Коэффициент корреляцииВторая формула коэффициента корреляции:
- 5. Коэффициент корреляцииТретья формула коэффициента корреляции:
- 6. Пример коэффициент корреляции Пример Психолог просит
- 7. Пример коэффициент корреляции Пример Для подсчета
- 8. Пример коэффициент корреляции Пример Подсчет совпадений
- 9. Пример коэффициент корреляции Пример Возьмем число
- 10. Пример коэффициент корреляции Пример Возьмем число
- 11. Пример коэффициент корреляции Пример Возьмем число
- 12. Пример коэффициент корреляции Пример Возьмем число
- 13. Пример коэффициент корреляции Пример Подсчет инверсий
- 14. Пример коэффициент корреляции Пример Возьмем число
- 15. Пример коэффициент корреляции Пример Возьмем число
- 16. Пример коэффициент корреляции Пример Возьмем число
- 17. Пример коэффициент корреляции Пример Возьмем число
- 18. Пример коэффициент корреляции Пример Возьмем число
- 19. Пример коэффициент корреляции Пример Возьмем число
- 20. Пример коэффициент корреляции Пример Возьмем число
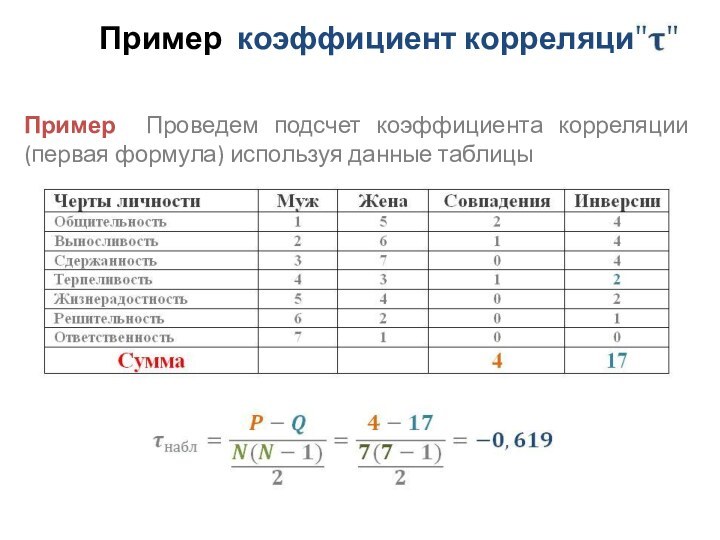
- 21. Пример коэффициент корреляции Пример Проведем подсчет коэффициента корреляции (первая формула) используя данные таблицы
- 22. Пример коэффициент корреляции Пример Проведем подсчет коэффициента корреляции (вторая формула) используя данные таблицы
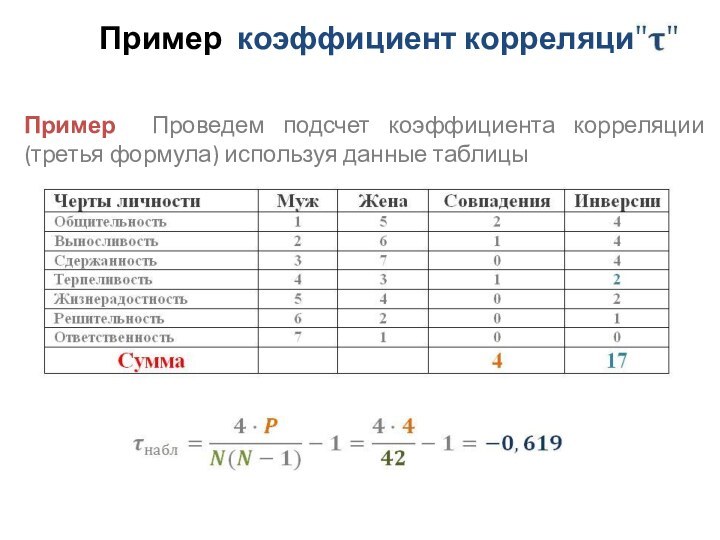
- 23. Пример коэффициент корреляции Пример Проведем подсчет коэффициента корреляции (третья формула) используя данные таблицы
- 24. Условия применения коэффициента корреляции Сравниваемые признаки
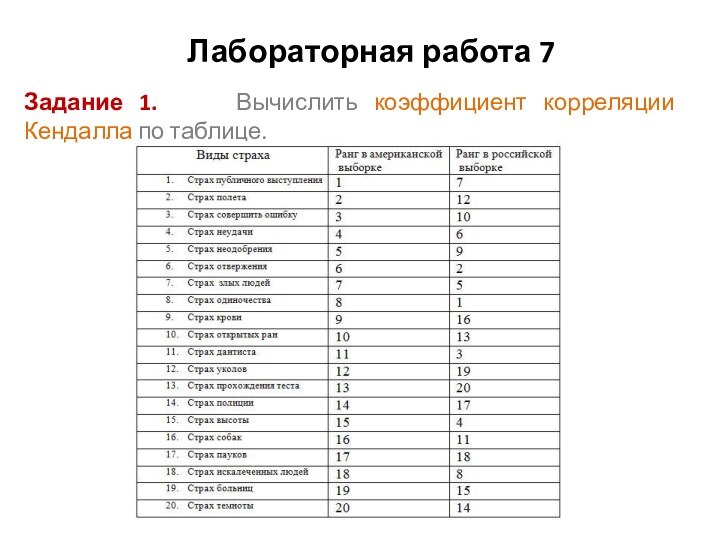
- 25. Лабораторная работа 7 Задание 1. Вычислить коэффициент корреляции Кендалла по таблице.
- 26. Лабораторная работа 7Задание 2. Вычислить коэффициент корреляции
- 27. Скачать презентацию
- 28. Похожие презентации
Коэффициент корреляцииКоэффициент корреляции (тау) Кендалла относиться к числу непараметрических, т.е. при вычислении этого коэффициента не играет роли характер распределения сравниваемых переменных. Коэффициент предназначен для работы с данными полученными в ранговой шкале.
















Слайд 3
Коэффициент корреляции
Подсчет коэффициента может осуществляться по трем тождественным
формулам. Первая формула:
Слайд 6
Пример коэффициент корреляции
Пример Психолог просит супругов проранжировать
семь личностных черт, имеющих определяющее значение для семейного благополучия.
Задача заключается в том, чтобы определить, в какой степени совпадают оценки супругов по отношению к ранжируемым качествам.
Слайд 7
Пример коэффициент корреляции
Пример Для подсчета коэффициента корреляции
необходимо упорядочить «оценки мужа» по возрастанию рангов. Соответственно
этому поменяются местами как сами черты, так и соответствующие ранги «оценки жены».
Слайд 8
Пример коэффициент корреляции
Пример Подсчет совпадений происходит следующим
образом: возьмем самое верхнее число столбца «жена» - 5
. Подсчитаем сколько чисел больших 5 встречаются ниже в этом столбце. Это числа 6, 7. число совпадений равно 2.
Слайд 9
Пример коэффициент корреляции
Пример Возьмем число столбца «жена»
- 6 . Подсчитаем сколько чисел больших 6 встречаются
ниже в этом столбце. Это число 7, число совпадений равно 1.
Слайд 10
Пример коэффициент корреляции
Пример Возьмем число столбца «жена»
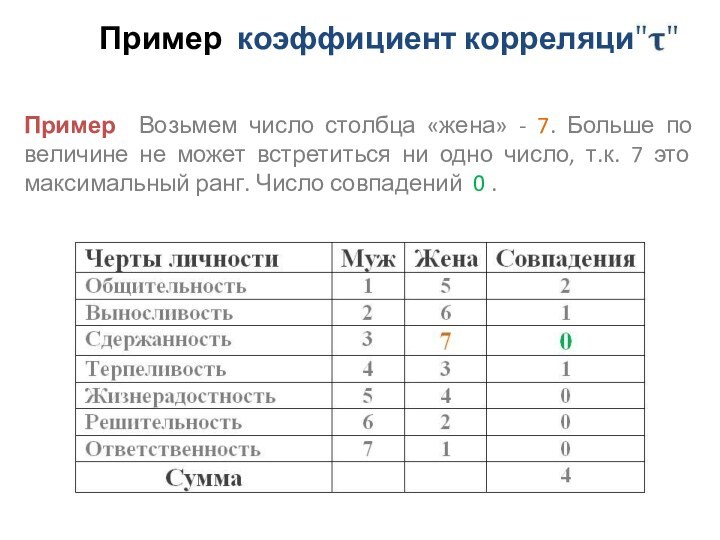
- 7. Больше по величине не может встретиться ни
одно число, т.к. 7 это максимальный ранг. Число совпадений 0 .
Слайд 11
Пример коэффициент корреляции
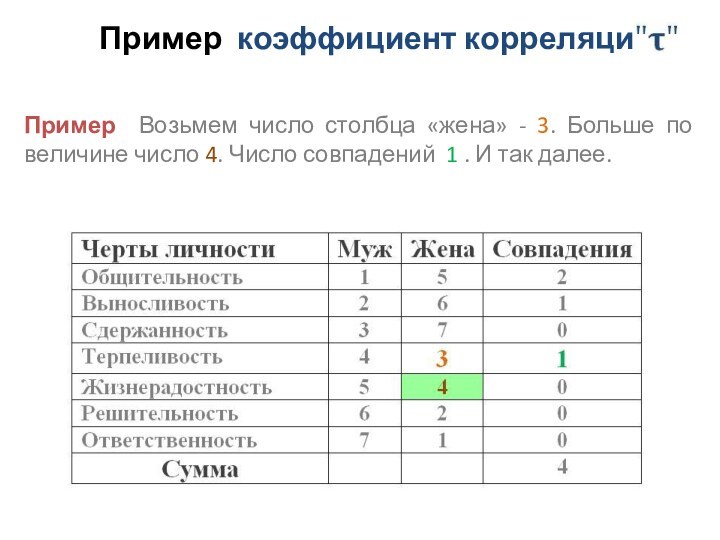
Пример Возьмем число столбца «жена»
- 3. Больше по величине число 4. Число совпадений
1 . И так далее.
Слайд 12
Пример коэффициент корреляции
Пример Возьмем число столбца «жена»
- 3. Больше по величине число 4. Число совпадений
1 . И так далее.
Слайд 13
Пример коэффициент корреляции
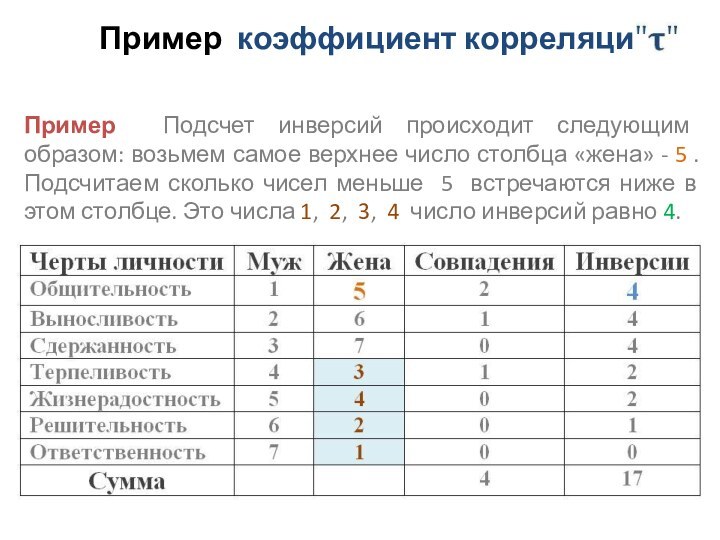
Пример Подсчет инверсий происходит следующим
образом: возьмем самое верхнее число столбца «жена» - 5
. Подсчитаем сколько чисел меньше 5 встречаются ниже в этом столбце. Это числа 1, 2, 3, 4 число инверсий равно 4.
Слайд 14
Пример коэффициент корреляции
Пример Возьмем число столбца «жена»
- 6 . Подсчитаем сколько чисел меньше 6 встречаются
ниже в этом столбце. Это числа 1, 2, 3, 4 число инверсий равно 4.
Слайд 15
Пример коэффициент корреляции
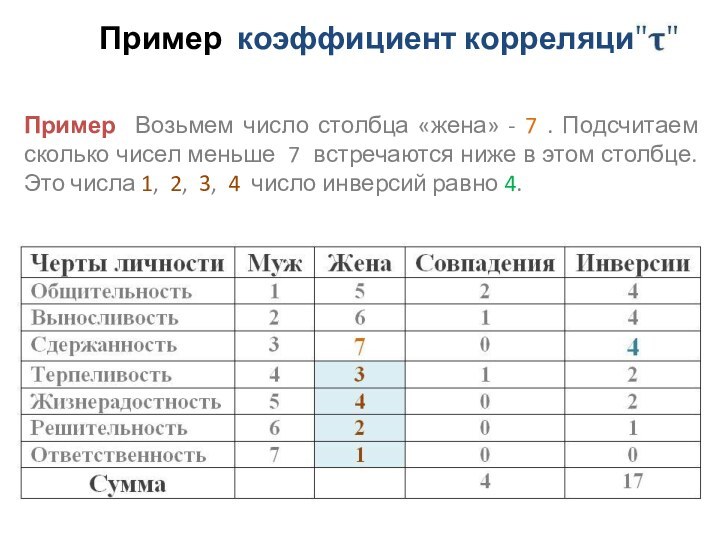
Пример Возьмем число столбца «жена»
- 7 . Подсчитаем сколько чисел меньше 7 встречаются
ниже в этом столбце. Это числа 1, 2, 3, 4 число инверсий равно 4.
Слайд 16
Пример коэффициент корреляции
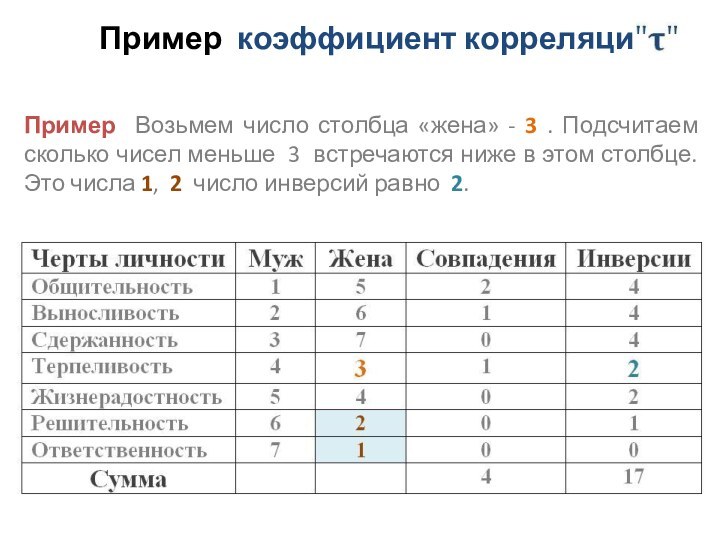
Пример Возьмем число столбца «жена»
- 3 . Подсчитаем сколько чисел меньше 3 встречаются
ниже в этом столбце. Это числа 1, 2 число инверсий равно 2.
Слайд 17
Пример коэффициент корреляции
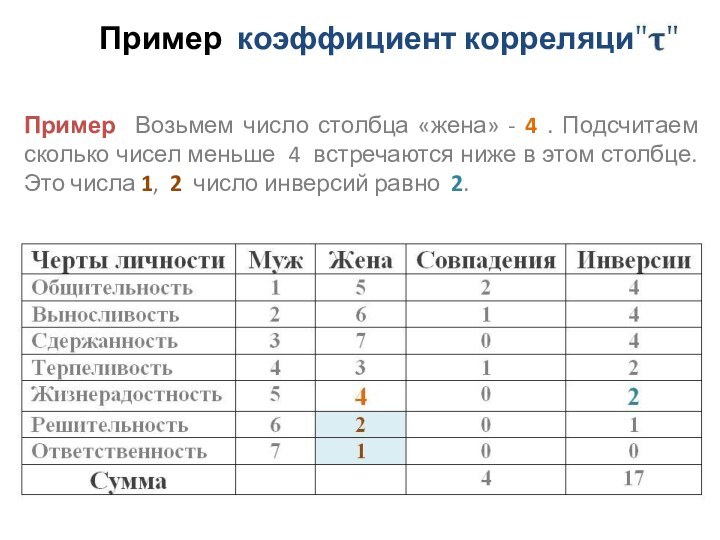
Пример Возьмем число столбца «жена»
- 4 . Подсчитаем сколько чисел меньше 4 встречаются
ниже в этом столбце. Это числа 1, 2 число инверсий равно 2.
Слайд 18
Пример коэффициент корреляции
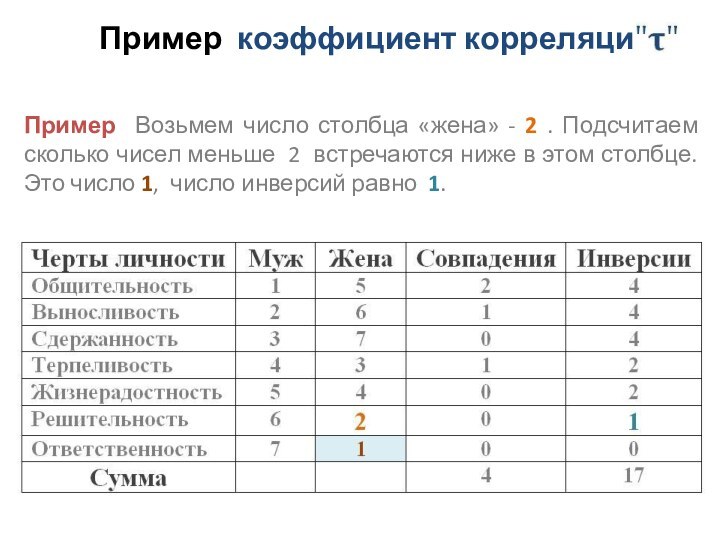
Пример Возьмем число столбца «жена»
- 2 . Подсчитаем сколько чисел меньше 2 встречаются
ниже в этом столбце. Это число 1, число инверсий равно 1.
Слайд 19
Пример коэффициент корреляции
Пример Возьмем число столбца «жена»
- 1 . Меньше числа не может быть, так
как это минимальный ранг. Число инверсий равно 0.
Слайд 20
Пример коэффициент корреляции
Пример Возьмем число столбца «жена»
- 1 . Меньше числа не может быть, так
как это минимальный ранг. Число инверсий равно 0.
Слайд 21
Пример коэффициент корреляции
Пример Проведем подсчет коэффициента корреляции
(первая формула) используя данные таблицы
Слайд 22
Пример коэффициент корреляции
Пример Проведем подсчет коэффициента корреляции
(вторая формула) используя данные таблицы
Слайд 23
Пример коэффициент корреляции
Пример Проведем подсчет коэффициента корреляции
(третья формула) используя данные таблицы
Слайд 24
Условия применения коэффициента корреляции
Сравниваемые признаки должны быть измерены
в порядковой шкале.
Число варьирующих признаков в сравниваемых переменных X
и Y должно быть одинаковым.Величина коэффициента Кендалла независима от закона распределения величин X и Y.
При расчетах этого коэффициента не допускается использование одинаковых рангов.
Слайд 26
Лабораторная работа 7
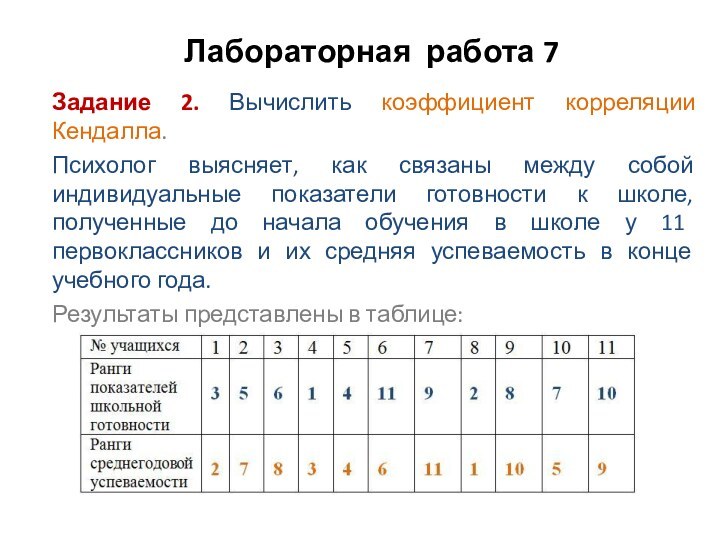
Задание 2. Вычислить коэффициент корреляции Кендалла.
Психолог
выясняет, как связаны между собой индивидуальные показатели готовности к
школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года.Результаты представлены в таблице: