- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Линейная алгебра и аналитическая геометрия
Содержание
- 2. Кафедра математики и моделирования
- 3. Курс лекций по линейной алгебре и
- 4. оглавлениеОпределители2. Элементы теории матриц3. Системы линейных уравнений4.Элементы векторной алгебры
- 5. Оглавление(продолжение)5.Прямые и плоскости6. Кривые второго порядка7.Поверхности второго порядка8.Замечательные кривые9.Комплексные числа
- 6. Лекция1. Определители Выражение
- 7. ОпределителиЧисла
- 8. Определители
- 9. Определители третьего порядкаВыражениеназывается определителем 3-гопорядка.
- 10. минорМинором элемента определителя 3-го порядка называется
- 11. Обозначение минора Минор элемента , стоящего на пересечении i-й строки и j-го столбца определителя, обозначают Мij.
- 12. Алгебраическое дополнениеАлгебраическим дополнениемэлемента определителя
- 13. Алгебраическое дополнение (продолжение)расположен на
- 14. В ы б
- 15. теорема разложения Определитель 3-го порядка равенсумме парных
- 16. Теорема разложения
- 17. Свойства определителей1.Определитель не меняет своегозначения
- 18. Свойства определителей(продолжение) 3.Общий множитель элементов
- 19. Свойства определителей (продолжение)4.Определитель равен нулю, если он
- 20. Свойства определителей (продолжение)6.Значение определителя
- 21. Определители высших порядков Выражениеназывается определителем 4-го порядка
- 22. Метод приведения к
- 23. Ключевые понятияОпределитель, элемент, строка, столбец,минор, алгебраическое дополнение, порядок определителя.
- 24. Вопросы для самопроверки по теме «Определители»1. Определители
- 25. Лекция 2. МатрицыМатрицей называется прямоугольная таблица чисел
- 26. Матрицы Матрица размера m×m называется квадратной.
- 27. Матрицы Квадратная матрица называется
- 28. Матрицы Определитель произведения квадратных матриц
- 29. Действия над матрицами.Суммой двух матриц одинаковой размерности
- 30. Действия над матрицами (продолжение)Произведением матрицы
- 31. Действия над матрицами (продолжение)
- 32. Действия над матрицами (продолжение) Произведением матрицы
- 33. Действия над матрицами (продолжение) стоящий
- 34. ИЗОБРАЖЕНИЕ МАТРИЦЫ
- 35. Обратная матрицаДве невырожденные квадратные матрицы одного
- 36. Формула обратной матрицы.
- 37. Единичная матрица
- 38. Свойства операций
- 39. Свойства операций
- 40. Р а н г м а
- 41. Теорема о ранге матрицы Ранг
- 42. Ранг матрицыРангом матрицы наз. порядок базисного минора. Если матрица нулевая ее ранг равен 0.
- 43. Элементарные преобразования матрицы.1.Умножение ряда на число не
- 44. Элементарные преобразования матрицы.4.Отбрасывание одного
- 45. Элементарные преобразования матрицы.Теорема: Элементарные преобразованияне меняют ранг
- 46. Ключевые понятияМатрица, размерность матрицы, операциинад матрицами, обратная матрица, ранг, элементарные преобразования матрицы.
- 47. Вопросы для самопроверки по теме «Матрицы»1. Понятие матрицы. Виды матриц.2. Невырожденная матрица.3. Линейные операции над матрицами.
- 48. Вопросы для самопроверки по теме «Матрицы»(продолжение)Свойства линейных операций над матрицами.Произведение матриц. Свойства.
- 49. Вопросы для самопроверки по теме «Матрицы»(продолжение)6. Необходимое
- 50. Вопросы для самопроверки по теме «Матрицы»(продолжение)8. Определители взаимно-обратных матриц.9. Ранг матрицы. Способы нахождения ранга матрицы.
- 51. Лекция3.Системы n линейных
- 52. Системы линейных уравнений Решением системы
- 53. Системы линейных уравненийРешить систему — значит найти
- 54. Системы линейных уравненийЕсли система имеет только одно
- 55. Системы линейных уравнений Если
- 56. Системы линейных уравненийСистема, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной).
- 57. Системы линейных уравнений Система, у
- 58. Системы линейных уравнений Однородная система всегда совместна,
- 59. Системы линейных уравнений Если число
- 60. Системы линейных уравнений Две системы,
- 61. Системы линейных уравненийПреобразование, применение
- 62. Метод КрамераМ е т
- 63. М е т о д
- 64. Правило Крамера решения квадратных систем линейных
- 65. Матричный метод решения систем Рассмотрим матрицы:Х = А-1·В
- 66. Л е к ц
- 67. М е т о д Г а у с с а
- 68. Метод Гаусса (продолжение)
- 69. Однородные системы
- 70. Теорема о совместности
- 71. Ключевые понятияЭлементарные преобразования надматрицей системы, прямой и обратныйход, однородные системы, фундаментальная система решений.
- 72. Ключевые понятияСистема уравнений, решение, общеерешение, частное решение, совместностьи несовместность системы, однородная инеоднородная системы.
- 73. Вопросы для самопроверки по теме «Системы
- 74. Вопросы для самопроверки по теме «Системы
- 75. Вопросы для самопроверки по теме «Системы
- 76. Л е к ц и я 5.
- 77. В е к т о р ы.
- 78. О с н о в н ы
- 79. О с н о в н ы
- 80. О с н о в н ы
- 81. Линейные операции над векторами Линейными
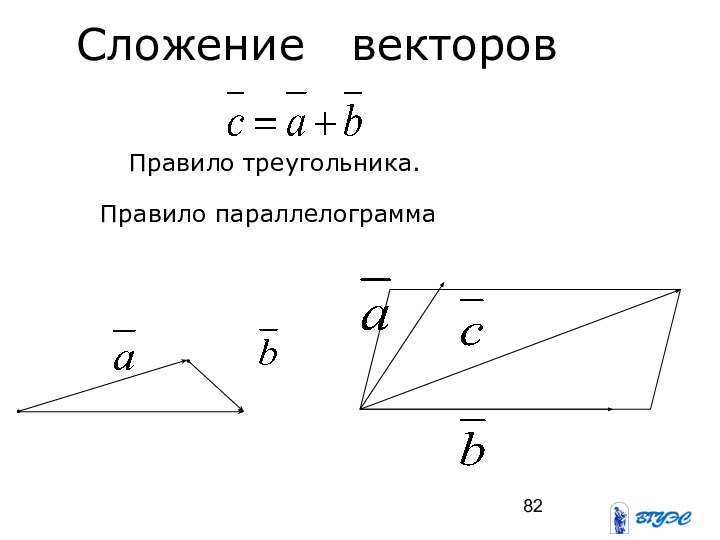
- 82. Сложение векторовПравило треугольника.Правило параллелограмма
- 83. Сумма нескольких векторов
- 84. Противоположные векторы
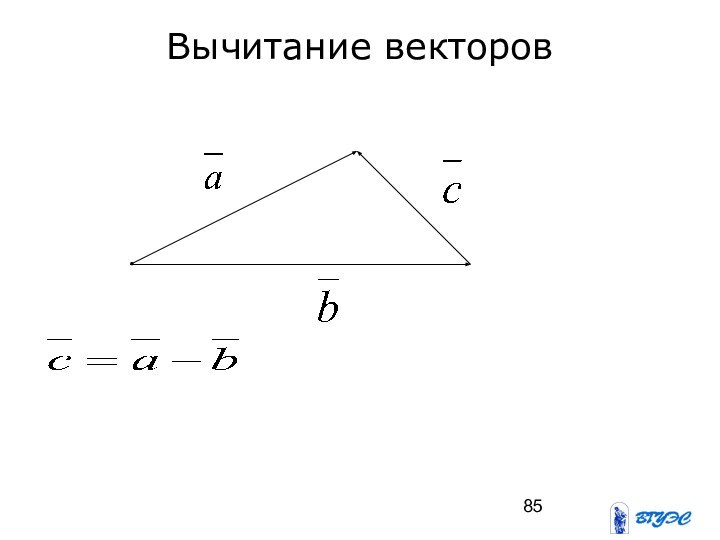
- 85. Вычитание векторов
- 86. Умножение вектора на число Произведением вектора
- 87. Умножение вектора на число
- 88. Пример В треугольнике ABC сторона
- 89. Проекция вектора на ось
- 90. Координаты вектора К о о р
- 91. Координатные векторыZYX
- 92. Разложение вектора на составляющиеOXYZ
- 93. Ключевые понятияВектор, модуль вектора, коллинеарность,компланарность, сложение и вычетаниевекторов, проекция вектора на ось.
- 94. Лекция6.Свойства линейных операций над векторами
- 95. Свойства линейных операций над векторами(продолжение)
- 96. Свойства линейных операций над векторами(продолжение)
- 97. Свойства линейных операций над векторами(продолжение)
- 98. Орт. Орт вектора.О р т о м
- 99. Единичный вектор Пусть дан вектор
- 100. Координаты единичного векторагде
- 101. ПримерНайти косинусы углов, которые, вектор
- 102. Б а з и с Базисом
- 103. Б а з и сБазисом на плоскости
- 104. Разложение вектора по базису Каждый
- 105. Модуль вектора
- 106. Коллинеарные векторы Векторы
- 107. Коллинеарные векторыОбозначение :
- 108. Условие коллинеарности
- 109. Условие коллинеарности двух векторов (продолжение) гдеи
- 110. Направляющие косинусы вектора
- 111. Направляющие косинусы вектора
- 112. Ключевые понятияОрт, координаты, базис, разложениевектора по
- 113. Лекция 7. Деление отрезка в данном отношении .
- 114. Скалярное произведение векторовСкалярным произведением векторовназывается
- 115. Скалярное произведение векторов
- 116. Физический смысл скалярного произведения
- 117. Физический смысл скалярного произведения
- 118. Угол между векторами
- 119. Проекция вектора на вектор
- 120. Свойства скалярного произведения
- 121. Свойства скалярного произведения (продолжение)
- 122. Свойства скалярного произведения (продолжение)
- 123. ПримерДан вектор, причем,,уголмежду векторамииравенНайти модуль вектораРешениеТак какито
- 124. Ключевые понятияСкалярное произведение векторов,физический
- 125. Лекция8.Векторное произведение векторовВекторным произведением двух векторовназывается
- 126. Обозначение векторного произведения векторов
- 127. Физический смысл векторного произведенияOM
- 128. Физический смысл векторного произведенияЕсли
- 129. Понятие «правой» тройки векторов Тройку векторов
- 130. ПримерНайти векторное произведение векторовРешение
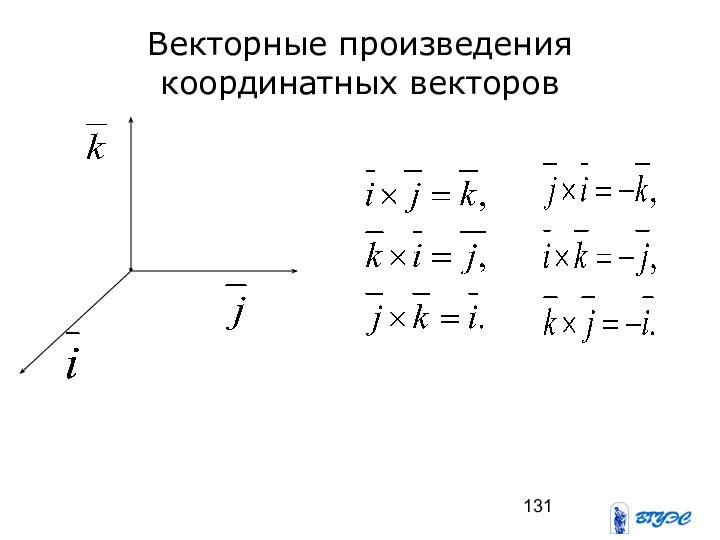
- 131. Векторные произведения координатных векторов
- 132. Площадь параллелограмма
- 133. Площадь треугольника
- 134. Свойства векторного произведенияилииилиили
- 135. Свойства векторного произведения
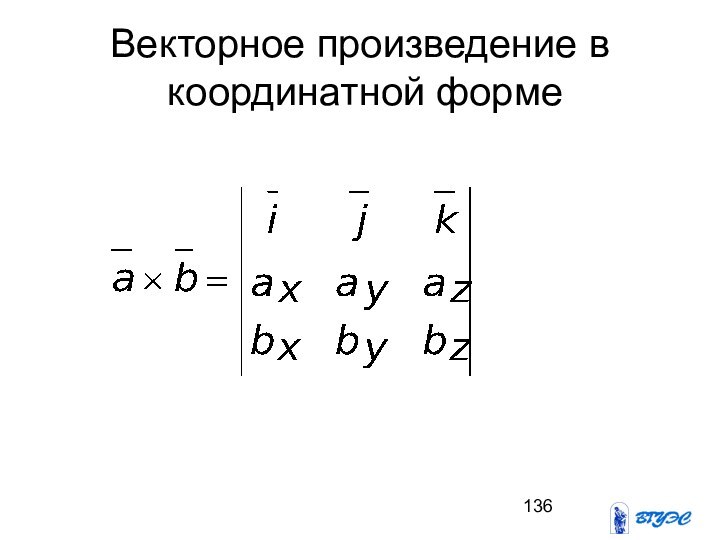
- 136. Векторное произведение в координатной форме
- 137. ПримерНайтиеслиРешение
- 138. Ключевые понятияВекторное произведение
- 139. Лекция 9.
- 140. Смешанное произведение
- 141. Компланарные векторы Три вектора называются компланарными, если они лежат в одной или параллельных плоскостях.
- 142. Условие компланарности трёх векторовЕсликомпланарны, то Элементами определителя являются координатывекторов
- 143. Объём параллелепипеда
- 144. Объём тетраэдра
- 145. Ключевые понятияСмешанное произведение векторов ,
- 146. Вопросы для самопроверки по теме «Векторы»1. Векторные
- 147. Вопросы для самопроверки по теме «Векторы» (продолжение)5.
- 148. Вопросы для самопроверки по теме «Векторы» (продолжение)9.
- 149. Вопросы для самопроверки по теме «Векторы» (продолжение)13.
- 150. Прямая на плоскости
- 151. Общее уравнение
- 152. Уравнение в отрезках
- 153. Каноническое уравнение
- 154. Уравнение прямой, проходящей через две точки
- 155. Параметрические уравнения
- 156. С угловым коэффициентом
- 157. Угол между двумя прямыми
- 158. Расстояние от точки до прямой
- 159. Ключевые понятияПрямая, нормаль, направляющий вектор,угол между
- 160. Вопросы для самопроверки по теме «Прямая на
- 161. Лекция10.Кривые второго порядка. Общее уравнение кривой второго порядка имеет вид
- 162. Кривые второго порядка. Уравнение такого вида может
- 163. Эллипс Эллипсом называется геометрическое место
- 164. Уравнение эллипса
- 165. Эллипс
- 166. Определение гиперболыГиперболой называетсягеометрическое место точек,разность расстояний которых от двухданных точек плоскости, называемыхфокусами, есть величина постоянная
- 167. Уравнение гиперболы
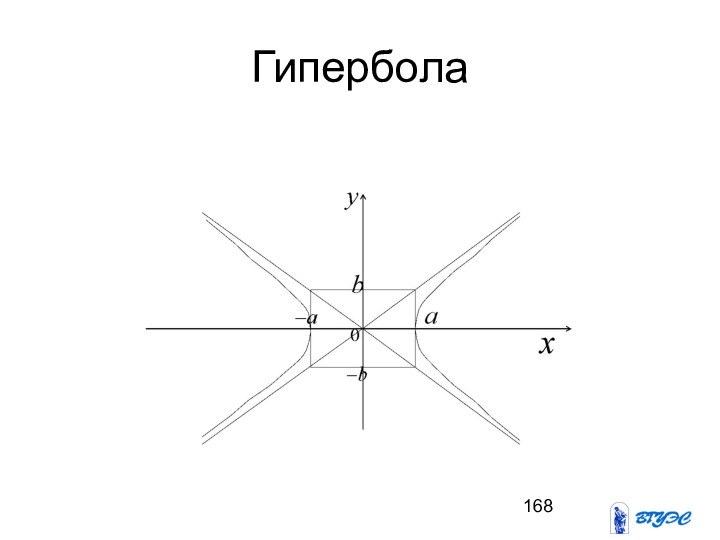
- 168. Гипербола
- 169. Лекция11.Определение параболы Параболой
- 170. Ключевые понятия Парабола, вершина, фокус, директриса , ось параболы.
- 171. Уравнение параболы
- 172. Парабола
- 173. Парабола
- 174. Ключевые понятияЭллипс, гипербола, окружность,фокусы, оси, эксцентриситет.
- 175. Вопросы для самопроверки по теме «Кривые второго
- 176. Вопросы для самопроверки по теме «Кривые второго
- 177. Полярные координаты
- 178. Лекция12.Плоскость
- 179. Общее уравнение
- 180. Уравнение в отрезках
- 181. Уравнение через три точки
- 182. Угол между плоскостями
- 183. Условие параллельности плоскостей
- 184. Условие перпендикулярности плоскостей
- 185. Расстояние от точки до плоскости
- 186. Ключевые понятияПлоскость, угол между
- 187. Вопросы для самопроверки по теме «Плоскость»1.Общее уравнение
- 188. Лекция13.Прямая в пространстве
- 189. Параметрические уравнения
- 190. Уравнение прямой, проходящей через две точки
- 191. Общие уравнения прямой
- 192. Угол между прямыми
- 193. Параллельность прямыхЕсли то
- 194. Перпендикулярность прямыхЕсли то
- 195. Угол между прямой и плоскостью
- 196. Условие параллельности прямой и плоскостиЕсли то
- 197. Условие перпендикулярности прямой и плоскостиЕсли
- 198. Ключевые понятияПрямая в пространстве, угол междупрямыми в пространстве, параллельность прямых, перпендикулярность прямых,угол между прямой и плоскостью.
- 199. Вопросы для самопроверки по теме «Прямая в
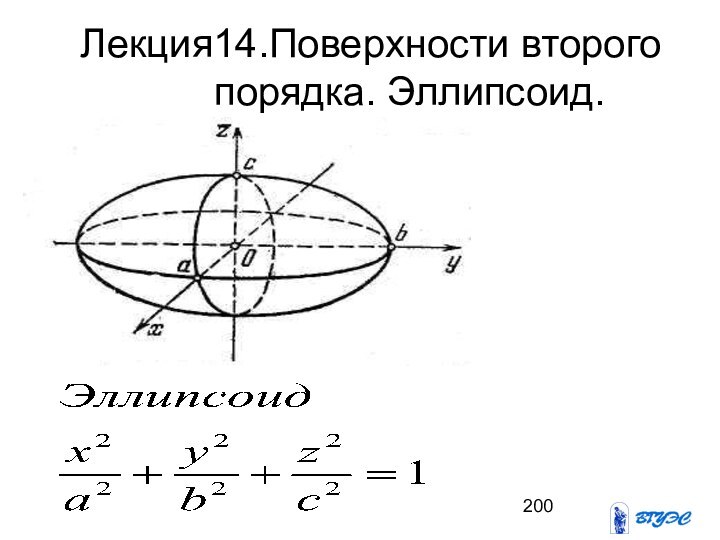
- 200. Лекция14.Поверхности второго порядка. Эллипсоид.
- 201. Цилиндрические поверхности Цилиндрической поверхностью
- 202. Цилиндрические поверхностиЕсли направляющая цилиндрической поверхности
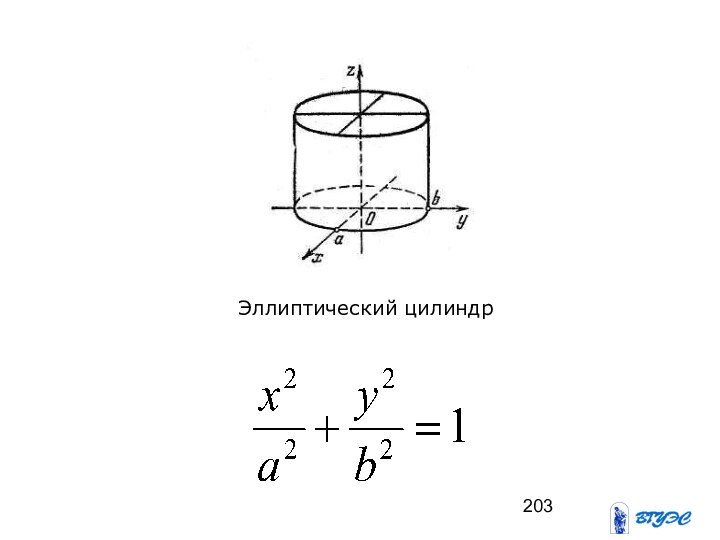
- 203. Эллиптический цилиндр
- 204. Конические поверхности Конической поверхностью называется поверхность, составленная
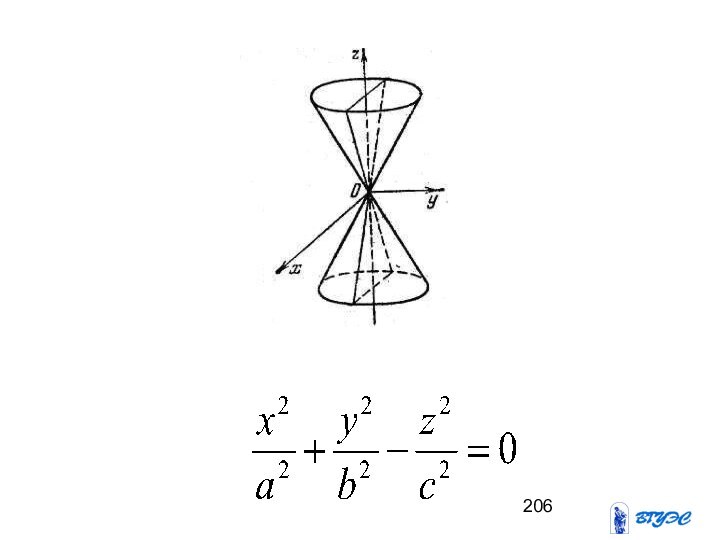
- 205. Конус
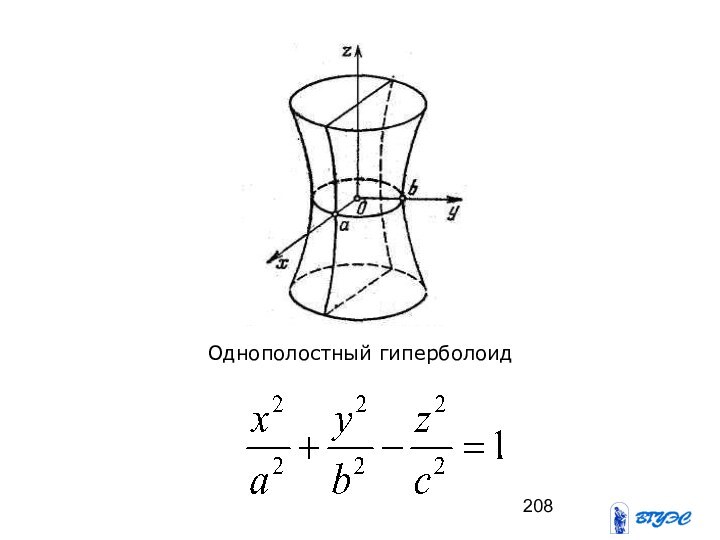
- 207. Однополостный гиперболоид
- 208. Однополостный гиперболоид
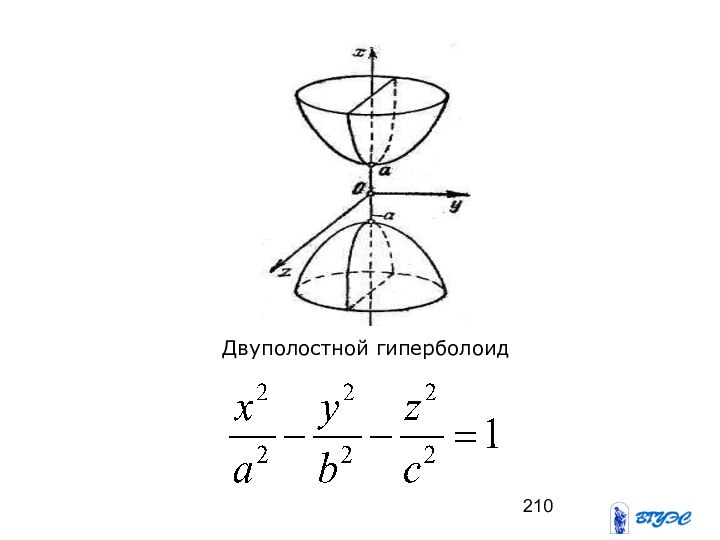
- 209. Двуполостный гиперболоид
- 210. Двуполостной гиперболоид
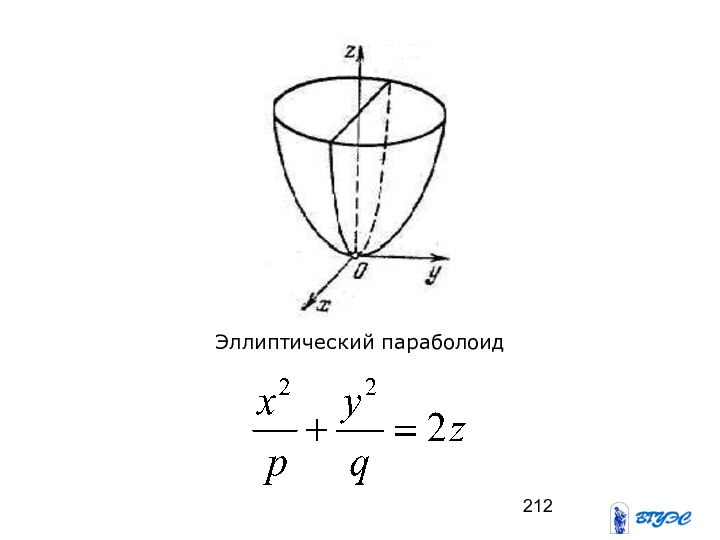
- 211. Эллиптический параболоид
- 212. Эллиптический параболоид
- 213. Гиперболический параболоид
- 214. Ключевые понятияПоверхность, эллипсоид, конус,цилиндр, виды цилиндров, однополостный гиперболоид, двуполостный гиперболоид,параболоид.
- 215. Вопросы для самопроверки по теме «Поверхности второго
- 216. Лекция15. Некоторые кривые
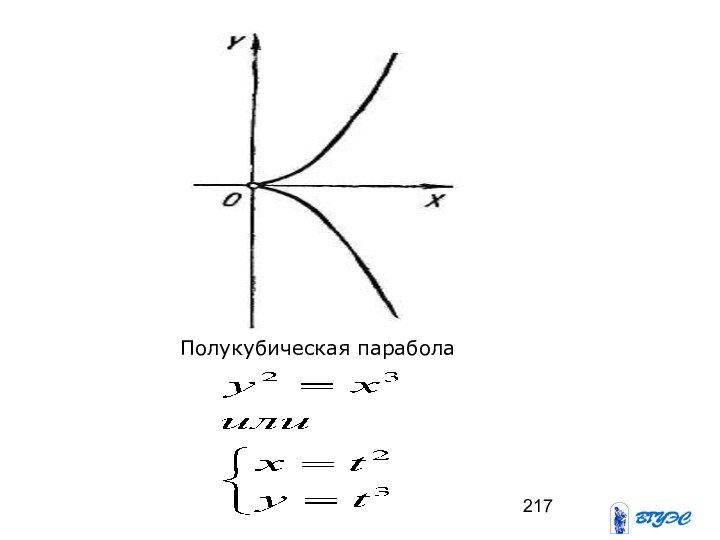
- 217. Полукубическая парабола
- 218. Кривая Гаусса
- 219. Декартов листили
- 220. Циссоида Диоклесаили
- 221. Лемниската Бернулли
- 222. Циклоида
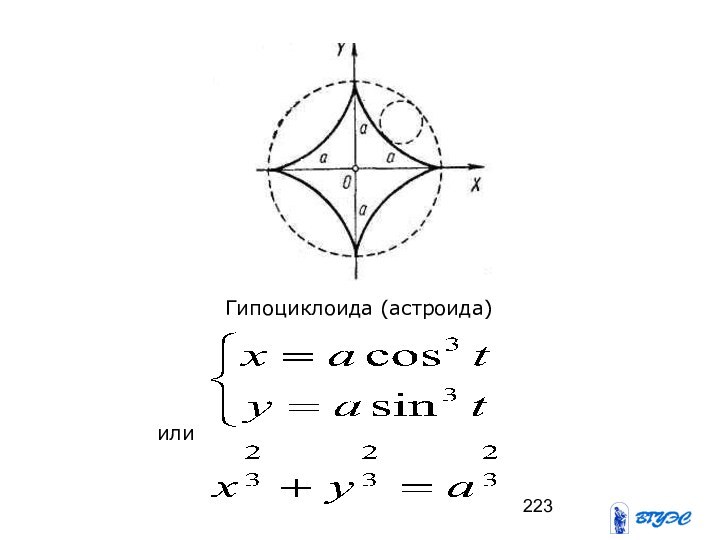
- 223. Гипоциклоида (астроида)или
- 225. Ключевые понятияЗамечательные кривые, кривая Гаусса,Декартов лист,
- 226. Лекция16.Комплексные числа. Комплексным числом z называется
- 227. Комплексные числа (продолжение)называется алгебраической формой записи комплексного числа.
- 228. Комплексные числа (продолжение) Число x называется
- 229. Комплексные числа (продолжение) Если x=0, то
- 230. Комплексные числа (продолжение) Два комплексных числа
- 231. Комплексные числа (продолжение)Всякое комплексное число
- 232. Модуль комплексного числа Число
- 233. Тригонометрическая форма комплексного числа.
- 234. Действия над комплексными числами
- 235. Действия над комплексными числами(продолжение)
- 236. Действия над комплексными числами(продолжение)
- 237. Действия над комплексными числами(продолжение)
- 238. Формулы Муавра
- 239. Ключевые понятияМнимая единица, комплексное число,действительная и мнимая частикомплексного числа; алгебраическая,тригонометрическая и показательнаяформы комплексного числа.
- 240. Вопросы для самопроверки по теме «Комплексные числа»
- 241. Вопросы для самопроверки по теме «Комплексные числа»
- 242. Вопросы для самопроверки по теме «Комплексные числа»
- 243. Основная литература 1. Беклемишев Д.В. Курс аналитической
- 244. Основная литература 3. Краснов М.Л., Киселев А.И.,
- 245. Дополнительная литература 1. Выгодский М.Я. Справочник по
- 246. Дополнительная литература 3. Шипачев В.С. Основы высшей
- 247. Скачать презентацию
- 248. Похожие презентации




























































































































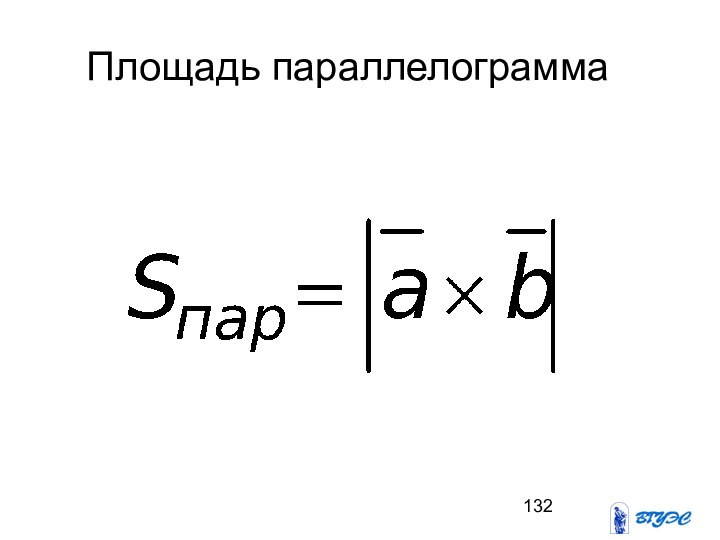
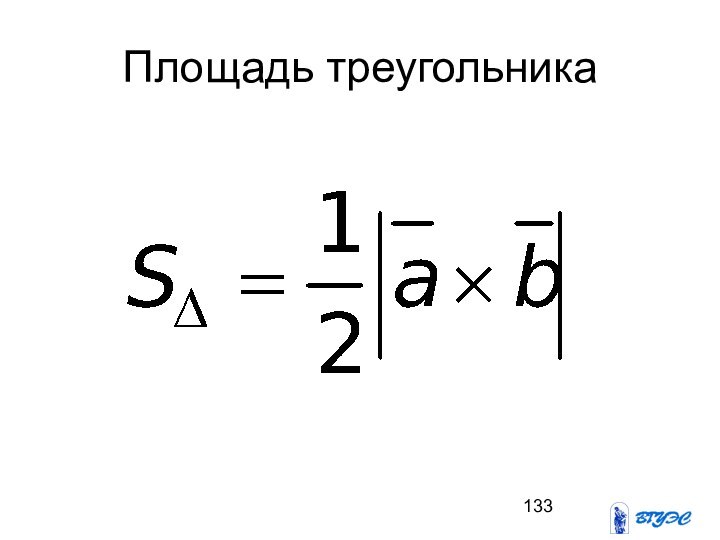















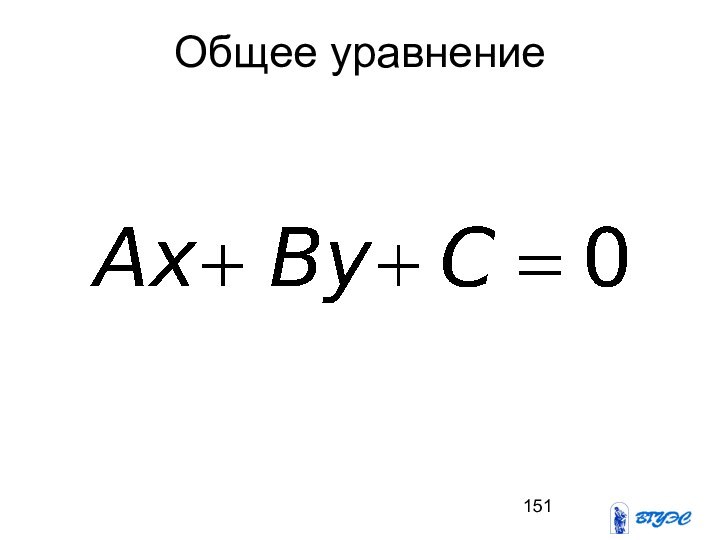
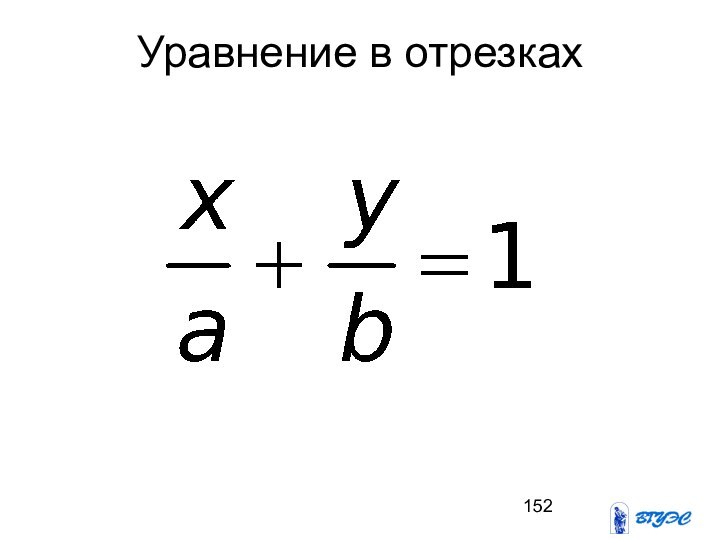
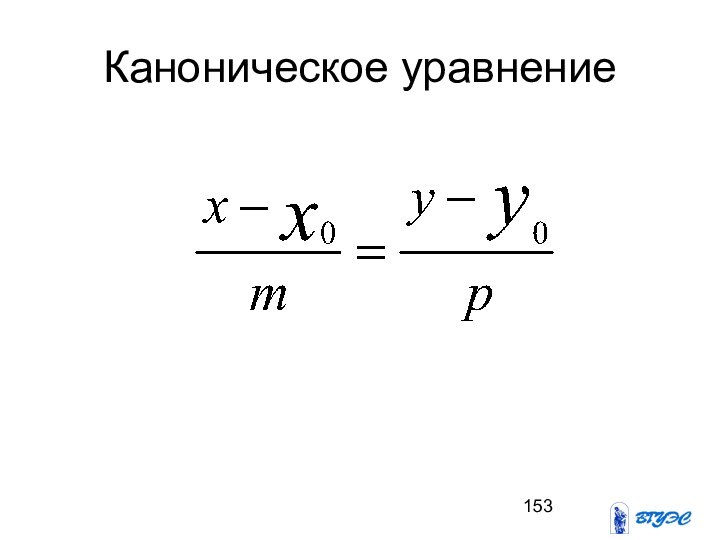

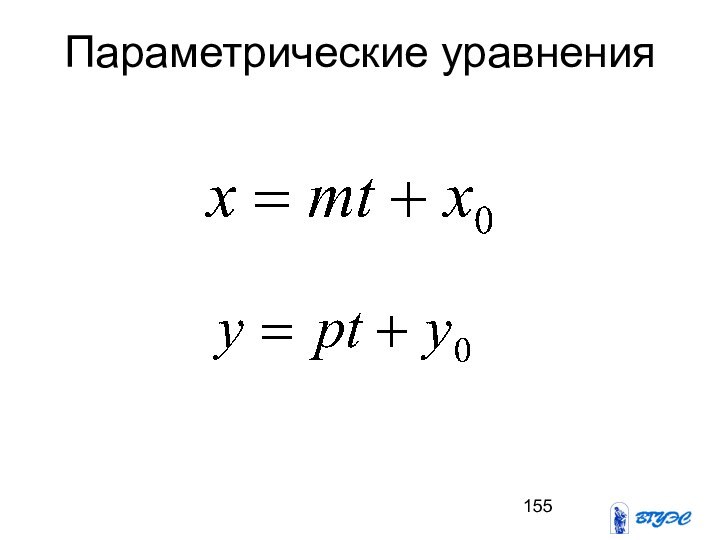








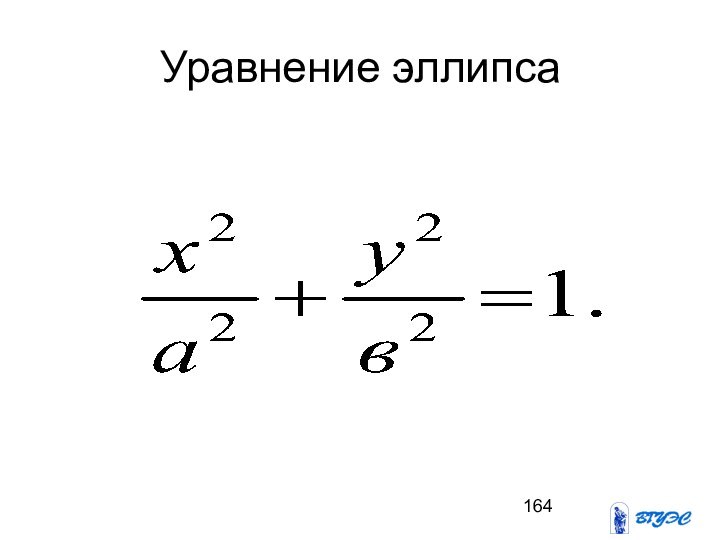


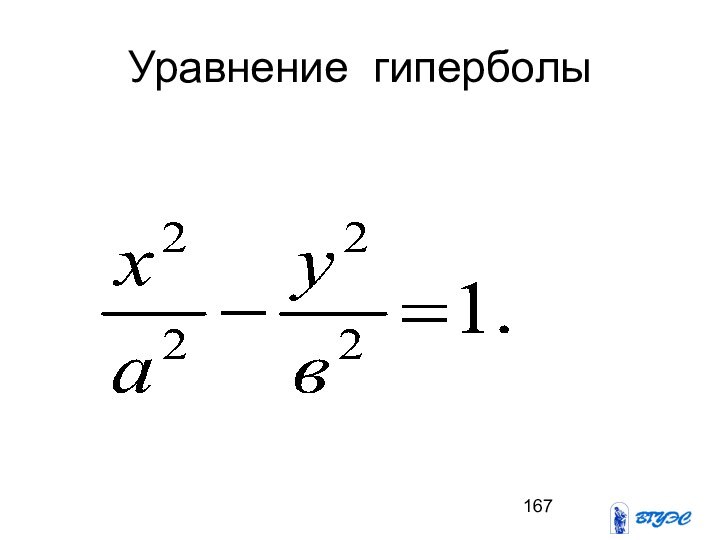


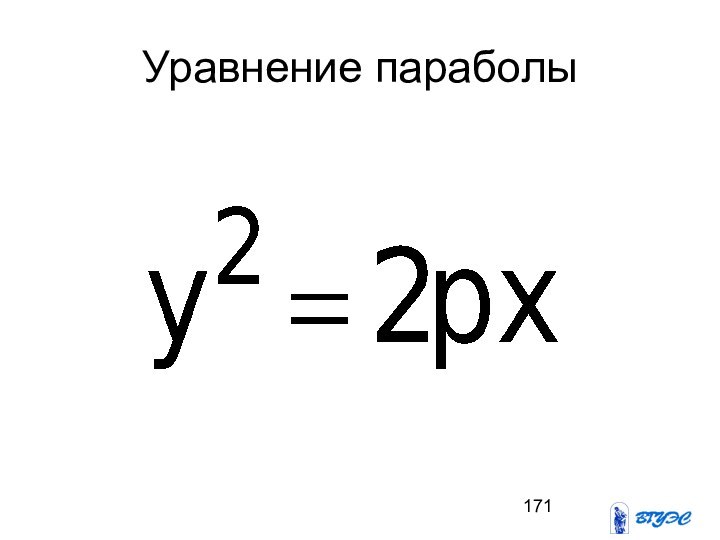







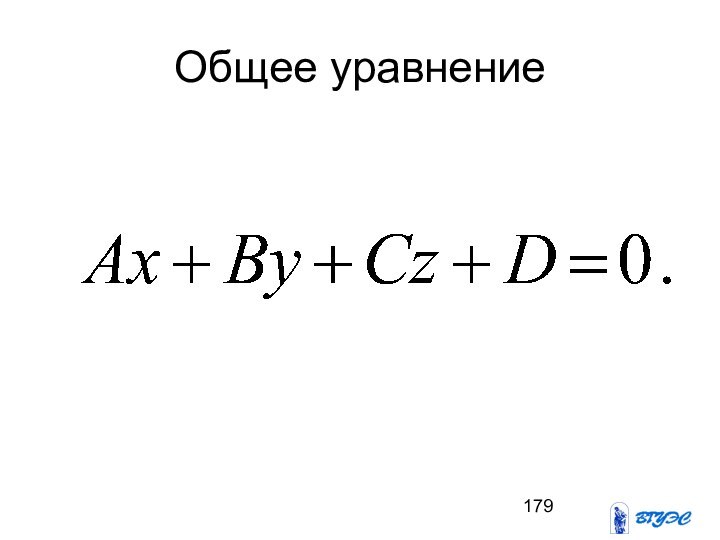



























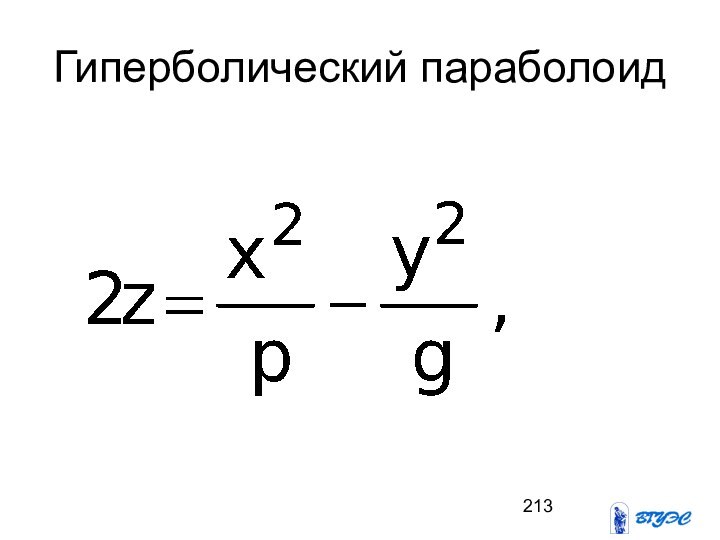
































Слайд 4
оглавление
Определители
2. Элементы теории матриц
3. Системы линейных уравнений
4.Элементы векторной
алгебры
Слайд 5
Оглавление(продолжение)
5.Прямые и плоскости
6. Кривые второго порядка
7.Поверхности второго порядка
8.Замечательные
кривые
9.Комплексные числа
Слайд 7
Определители
Числа
– это элементы
определителя. Индексы, стоящие внизу
соответствующего элемента, означают номер строки и номер столбца
определителя, на пересечении которых находится указанный элемент.
Слайд 8
Определители
Элементы
называют элементами главной диагонали определителя, а другие два элемента – соответственно элементами побочной диагонали.
Слайд 10
минор
Минором элемента определителя 3-го
порядка называется определитель
2-го
порядка, получающийся из данного
определителя вычёркиванием строки и
столбца,
в которых расположен элемент.
Слайд 11
Обозначение минора
Минор элемента , стоящего на
пересечении
i-й строки и j-го столбца
определителя, обозначают Мij.
Слайд 12
Алгебраическое дополнение
Алгебраическим дополнением
элемента определителя
3-го
порядка называется минор
этого
элемента, взятый со знаком плюс, если элемент
Слайд 13
Алгебраическое дополнение
(продолжение)
расположен на пересечении
строки
и столбца с четной
суммой
номеров, и со знаком минус, если c нечётной.
Слайд 14 В ы б о
р з н а к а
Для определителя 3-го
порядка знаки алгебраических дополнений определяются по таблице:
Слайд 15
теорема разложения
Определитель 3-го порядка равен
сумме парных произведений
элементов
какого-либо ряда
определителя на их алгебраические
дополнения (под рядом понимается
строка или
столбец)
Слайд 17
Свойства определителей
1.Определитель не меняет своего
значения при замене
каждой строки
соответствующим столбцом.
2.Определитель изменит знак ,если
поменять местами любые две
строки
или столбца.
Слайд 18
Свойства определителей(продолжение)
3.Общий множитель элементов
какого-либо ряда определителя
можно выносить за знак определителя.
Слайд 19
Свойства определителей
(продолжение)
4.Определитель равен нулю, если он
имеет два
одинаковых столбца или
строки.
5.Определитель равен нулю, если он
имеет нулевой
ряд.
Слайд 20
Свойства определителей
(продолжение)
6.Значение определителя не
изменится,
если к элементам строки
или
столбца прибавитьсоответствующие элементы другой
строки или столбца, умноженные на
одно число.
Слайд 22 Метод приведения к
треугольному виду
Метод приведения к треугольному
виду
заключается в такомпреобразовании данного
определителя, когда все элементы
его, лежащие по одну сторону одной
из его диагоналей, становятся
равными нулю.
Слайд 23
Ключевые понятия
Определитель, элемент,
строка, столбец,
минор, алгебраическое дополнение,
порядок
определителя.
Слайд 24
Вопросы для самопроверки по
теме «Определители»
1. Определители второго и
третьего порядков.
2. Свойства определителей.
3. Методы вычислений определителей.
4. Алгебраическое дополнение.
5.
Минор.
Слайд 25
Лекция 2. Матрицы
Матрицей называется прямоугольная
таблица чисел .
Если
матрица содержит m строк и n
столбцов, то говорят, что
матрица имеетразмерность .
Слайд 26
Матрицы
Матрица размера m×m называется квадратной.
Две матрицы считаются равными, если равны их размеры и
равны элементы, стоящие на одинаковых местах.
Слайд 27
Матрицы
Квадратная матрица называется невырожденной
(неособенной), если
её определитель отличен от нуля, и
вырожденной (особенной) , если определитель её равен нулю.
Слайд 28
Матрицы
Определитель произведения квадратных матриц
равен произведению определителей этих
матриц:
Слайд 29
Действия над матрицами.
Суммой двух матриц одинаковой размерности А
и В
называется матрица С той же размерности,
элементы которой
равны суммам элементов матриц A и B с одинаковыми индексами.
Слайд 30
Действия над матрицами
(продолжение)
Произведением матрицы
на
число α называется матрица ,
получающаяся
из матрицы Aумножением всех её элементов
на α .
Слайд 31
Действия над матрицами
(продолжение)
Разностью
двух матриц А и В
одинаковой размерностиназывается матрица A+(-B).
Слайд 32
Действия над матрицами
(продолжение)
Произведением матрицы
размера
на
матрицу размера называется матрица размера
, элемент которой ,
Слайд 33
Действия над матрицами
(продолжение)
стоящий в
i-ой строке и j-ом
столбце, равен
сумме произведенийэлементов i-ой строки матрицы A и
соответствующих элементов j-го столбца
матрицы B.
Слайд 35
Обратная матрица
Две невырожденные квадратные
матрицы одного и
того же порядка
называются обратными, если их
произведение, взятое в
любомпорядке, равно единичной матрице
того же порядка.
Слайд 39 Свойства операций
над матрицами
(продолжение)
4. (AB)C=A(BC)
5. A(B+C)=AB+AC
6. A+O=A
7. AE=EA=A
Слайд 40 Р а н г м а т
р и ц ы
Рангом матрицы называется порядок
наивысшего отличного от
нуляминора матрицы.
Ранг матрицы A обозначается:
R(A) или r(A) или rangA.
Слайд 41
Теорема о ранге матрицы
Ранг матрицы
равен максимальному числу
линейно – независимых столбцов матрицы. Максимальное число
линейно-независимых строк равно максимальному числу линейно-независимых столбцов.
Слайд 42
Ранг матрицы
Рангом матрицы наз. порядок базисного минора. Если
матрица нулевая ее ранг равен 0.
Слайд 43
Элементарные преобразования матрицы.
1.Умножение ряда на число не равное
0.
2. Перестановка строк или столбцов местами.
3.
Прибавление одной строки (или столбца) к другой, умноженной на число.
Слайд 44
Элементарные преобразования матрицы.
4.Отбрасывание одного из
двух одинаковых рядов.
5.Отбрасывание нулевого
ряда.
Слайд 45
Элементарные преобразования матрицы.
Теорема: Элементарные преобразования
не меняют ранг матрицы.
Матрицы, полученные с помощью
элементарных
преобразований наз.эквивалентными (~).
Слайд 46
Ключевые понятия
Матрица, размерность матрицы, операции
над матрицами, обратная матрица,
ранг,
элементарные преобразования матрицы.
Слайд 47
Вопросы для самопроверки
по теме «Матрицы»
1. Понятие матрицы. Виды
матриц.
2. Невырожденная матрица.
3. Линейные операции над матрицами.
Слайд 48
Вопросы для самопроверки
по теме «Матрицы»(продолжение)
Свойства линейных операций над
матрицами.
Произведение матриц. Свойства.
Слайд 49
Вопросы для самопроверки
по теме «Матрицы»(продолжение)
6. Необходимое и достаточное
условие
существования матрицы, обратной
данной.
7. Алгоритм нахождения матрицы, обратной данной.
Слайд 50
Вопросы для самопроверки
по теме «Матрицы»(продолжение)
8. Определители взаимно-обратных матриц.
9.
Ранг матрицы. Способы нахождения ранга матрицы.
Слайд 52
Системы линейных уравнений
Решением системы будем называть
упорядоченный набор чисел x1, x2, … , xn, обращающий
каждое уравнение системы в верное равенство.
Слайд 53
Системы линейных уравнений
Решить систему — значит найти все
ее решения или доказать, что ни одного решения нет.
Система,
имеющая решение, называется совместной.
Слайд 54
Системы линейных уравнений
Если система имеет только одно
решение,
то она называется
определенной.
Слайд 56
Системы линейных уравнений
Система, имеющая более чем одно
решение, называется неопределенной
(совместной и неопределенной).
Слайд 57
Системы линейных уравнений
Система, у которой
все
свободные члены равны нулю
(b1 = b2 =…= bn = 0), называется однородной.
Слайд 58
Системы линейных уравнений
Однородная система всегда совместна,
так как
набор из n нулей удовлетворяет
любому
уравнению такой системы.
Слайд 59
Системы линейных уравнений
Если число
уравнений системы
совпадает с числом неизвестных
, то система называется квадратной.
Слайд 60
Системы линейных уравнений
Две системы, множества
решений
которых совпадают, называются
эквивалентными или
равносильными.
Слайд 61
Системы линейных уравнений
Преобразование, применение
которого
превращает систему в новую
систему,эквивалентную исходной, называется
эквивалентным или равносильным
преобразованием.
Слайд 64 Правило Крамера решения квадратных систем линейных равнений
Если определитель матрицы A не
равен нулю, то система имеет
единственное
решение,определяемое формулами:
Здесь Δi – определитель n-го порядка, получающийся из определителя Δ матрицы A коэффициентов системы заменой i-го столбца столбцом свободных членов.
Слайд 66 Л е к ц и
я 4. Т е о р е м а
К р о н е к е р а - К а п е л л и
Для того чтобы система m
неоднородных линейных уравнений
с n неизвестными была совместной,
Необходимо и достаточно, чтобы
R(A)=R(B).
Слайд 70 Теорема о совместности
однородной системы
Для того чтобы однородная
системалинейных уравнений имела
нетривиальное решение, необходимо
и достаточно, чтобы ранг матрицы
этой системы был меньше числа
неизвестных n.
Слайд 71
Ключевые понятия
Элементарные преобразования над
матрицей системы, прямой и обратный
ход,
однородные системы,
фундаментальная система решений.
Слайд 72
Ключевые понятия
Система уравнений, решение, общее
решение, частное решение, совместность
и
несовместность системы, однородная и
неоднородная системы.
Слайд 73
Вопросы для самопроверки
по теме «Системы уравнений»
1. Система
линейных алгебраических уравнений. Решение системы.
2. Матричная форма записи СЛАУ.
Решение СЛАУ матричным способом.3. Правило Крамера.
Слайд 74
Вопросы для самопроверки
по теме «Системы уравнений»
(продолжение)
4.Однородные системы
уравнений.
5.Тривиальное решение.
6.Фундаментальная система решений
однородной СЛАУ.
Слайд 75
Вопросы для самопроверки
по теме «Системы уравнений»
(продолжение)
7. Теорема
Кронекера - Капелли.
8. Линейные преобразования.
Собственные значения и
собственныевекторы линейного преобразования.
Слайд 76 Л е к ц и я 5. В
е к т о р ы. О с н о
в н ы е п о н я т и я.
Вектором называется множество
всех направленных отрезков,
имеющих одинаковую длину и
направление.
Обозначают векторы символами
или , где А- начало, а B-конец
направленного отрезка .
Слайд 77 В е к т о р ы. О
с н о в н ы е п
о н я т и я. ( Продолжение)
Нулевым вектором (обозначается )
называется вектор, начало и конец
которого совпадают.
Слайд 78 О с н о в н ы е
п о н я т и я
(продолжение)
Расстояние между
началом и концом вектора называется его длиной, или
модулем или абсолютной величиной.
Слайд 79 О с н о в н ы е
п о н я т и я
(продолжение)
Векторы называются
коллинеарными,
если они расположены на одной прямой или
на параллельных прямых
Слайд 80 О с н о в н ы е
п о н я т и я
(продолжение)
Векторы
называютсякомпланарными, если они
параллельны одной плоскости.
Векторы называются равными,
если они сонаправлены и имеют
равные длины.
Слайд 81
Линейные операции над векторами
Линейными операциями
называют
операции сложения и
вычитания векторов и умножения вектора на
число.
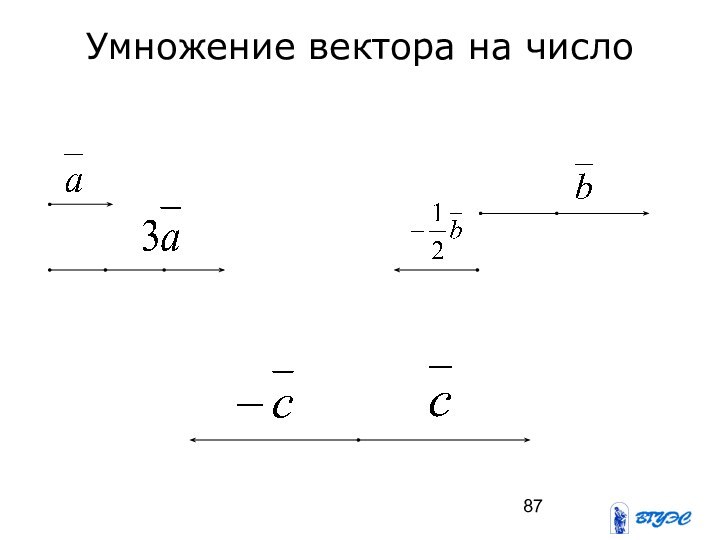
Слайд 86
Умножение вектора на число
Произведением вектора
на
действительное число
называется вектор (обозначают ),
определяемый следующими условиями:
1. ,
2. при и при
.
Слайд 88
Пример
В треугольнике ABC сторона AB
разделена на три равные части точками M и N.
Пусть , выразить вектор
через и .
Решение
Слайд 90
Координаты вектора
К о о р
д и н а т а м
ив е к т о р а н а з ы в а ю т с я
е г о п р о е к ц и и н а
о с и к о о р д и н а т.
Слайд 92
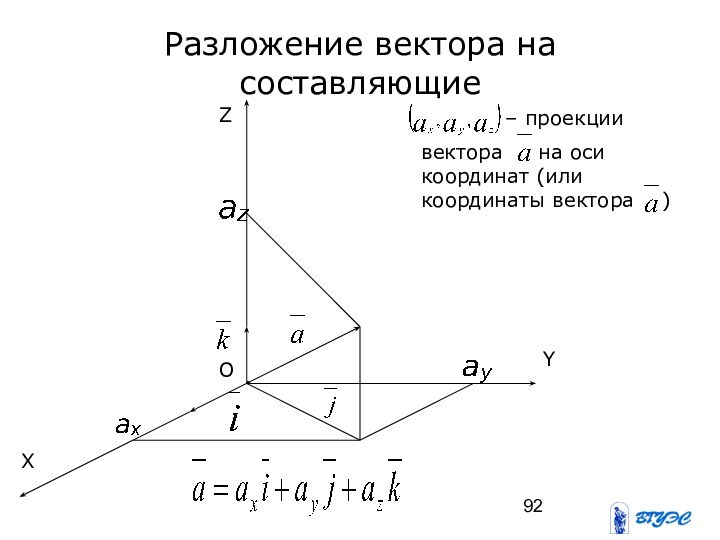
Разложение вектора на составляющие
O
X
Y
Z
– проекции
вектора на оси координат
(или координаты вектора )
Слайд 93
Ключевые понятия
Вектор, модуль вектора, коллинеарность,
компланарность, сложение и вычетание
векторов,
проекция вектора на ось.
Слайд 98
Орт. Орт вектора.
О р т о м
н а з ы в а е т с
я в е к т о ре д и н и ч н о й д л и н ы.
О р т о м в е к т о р а н а з ы в а е т с я
с о н а п р а в л е н н ы й е м у о р т.
Слайд 99
Единичный вектор
Пусть дан вектор .
Рассмотрим вектор
коллинеарный вектору , одинаково с
ним направленный , но имеющий длину, равную
единице. Будем называть этот вектор ортом
данного вектора .
Слайд 101
Пример
Найти косинусы углов, которые, вектор
составляет с
осями координат, если А (1,2,3) и В (2,4,5).
Решение.
Слайд 102
Б а з и с
Базисом
в пространстве называются
три некомпланарных вектора, взятых
в определенном порядке.
Слайд 103
Б а з и с
Базисом на плоскости называют
два
неколлинеарных вектора , взятых в
определенном
порядке; базисом на прямой называют любой ненулевой
вектор на этой прямой.
Слайд 104
Разложение вектора по базису
Каждый вектор
в пространстве, плоскости или на прямой может быть разложен
по базису пространства, плоскости или прямой соответственно, причем это разложение единственно.
Слайд 106
Коллинеарные векторы
Векторы
называются
коллинеарными, если они лежат
на
одной прямой, либо на параллельных прямых.
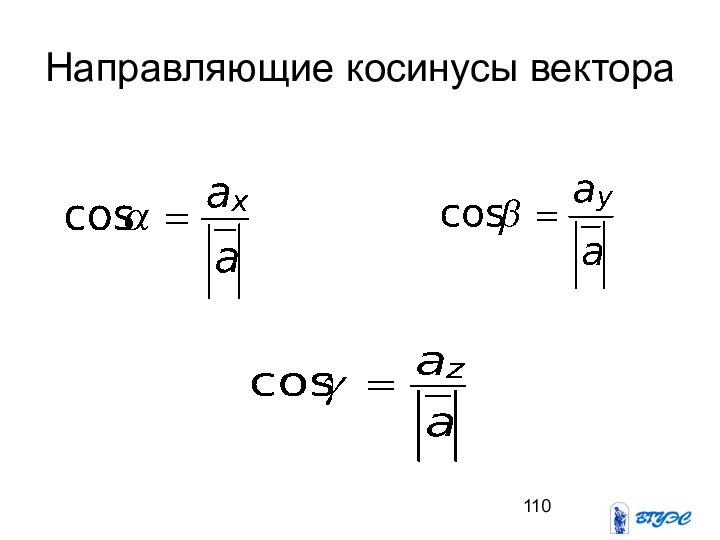
Слайд 112
Ключевые понятия
Орт, координаты, базис, разложение
вектора по
базису, направляющие
косинусы вектора.
Слайд 114
Скалярное произведение векторов
Скалярным произведением векторов
называется произведение
их
модулей на косинус
угла междуними.
Слайд 116
Физический смысл скалярного
произведения
Работа
постоянной силы на
прямолинейном участке пути равна
скалярному произведению вектора
силы на вектор перемещения.
Слайд 124
Ключевые понятия
Скалярное произведение векторов,
физический смысл
скалярного
произведения, угол между векторами,
проекция вектора на
вектор.
Слайд 125
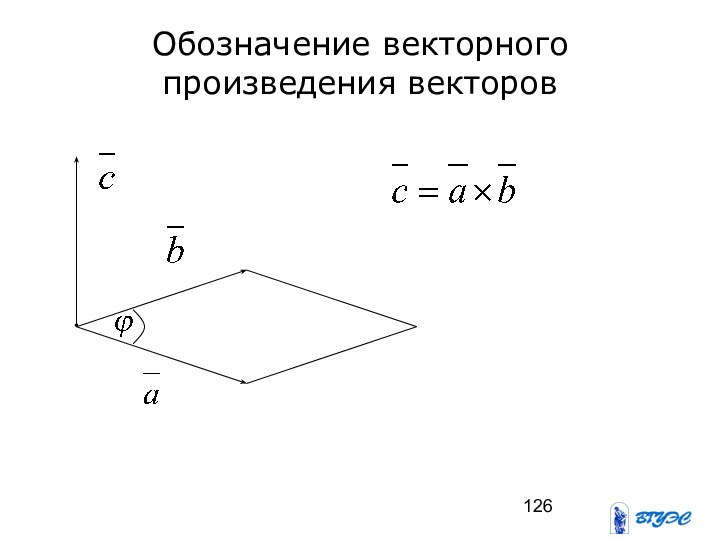
Лекция8.Векторное
произведение векторов
Векторным произведением двух векторов
называется вектор, который
обозначается
и определяется следующим образом:
где – длина этого вектора равна
произведению длин перемножаемых векторов на
Синус угла между ними.
Этот вектор перпендикулярен каждому из
векторов и образует с ними правую тройку.
Слайд 128
Физический смысл векторного произведения
Если
– сила, приложенная к точке М,
то момент этой
силы относительно точки О равен векторному произведению
векторов и .
Слайд 129
Понятие «правой» тройки векторов
Тройку векторов
называют правой, если
направление вектора
таково, что, смотря из его концавдоль вектора, поворот по кратчайшему пути от вектора
к вектору будет виден против движения часовой
стрелки.
Слайд 138
Ключевые понятия
Векторное произведение векторов,
физический смысл векторного
произведения, правая
и левая тройка векторов.
Слайд 139 Лекция 9.
Смешанное произведение
Смешанным
произведением трёхвекторов называется произведение
вида :
Слайд 141
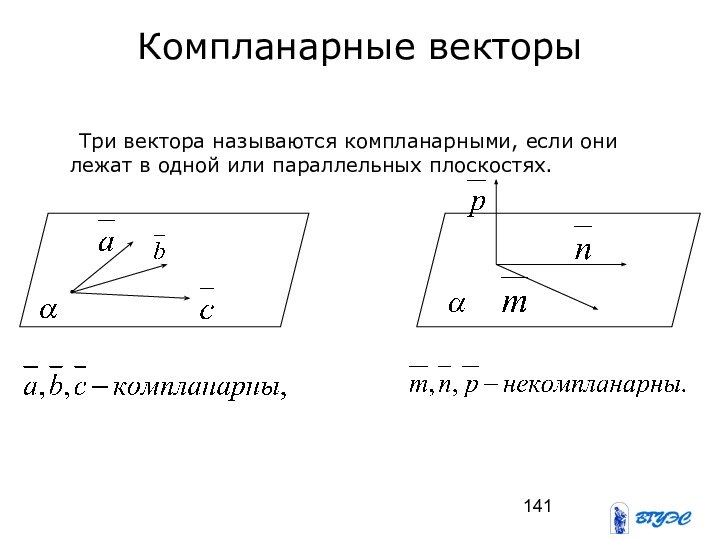
Компланарные векторы
Три вектора называются компланарными, если они лежат
в одной или параллельных плоскостях.
Слайд 142
Условие компланарности трёх векторов
Если
компланарны, то
Элементами определителя являются
координаты
векторов
Слайд 146
Вопросы для самопроверки
по теме «Векторы»
1. Векторные и скалярные
величины.
2. Векторы. Основные определения.
3. Равенство векторов. Орт.
4. Линейные операции
над векторами.
Слайд 147
Вопросы для самопроверки
по теме «Векторы»
(продолжение)
5. Линейно зависимые (независимые)
векторы.
6. Базис на плоскости и в пространстве.
7. Разложение вектора
по базису.8. Линейные операции над векторами в координатной форме.
Слайд 148
Вопросы для самопроверки
по теме «Векторы»
(продолжение)
9. Деление отрезка в
данном отношении.
10. Направляющие косинусы вектора.
11. Проекция вектора на ось.
12.Угол
между вектором и осью.
Слайд 149
Вопросы для самопроверки
по теме «Векторы»
(продолжение)
13. Скалярное произведение векторов.
Свойства.
14. Векторное произведение векторов.
15. Смешанное произведение векторов.
16. Компланарность векторов.
Необходимое и достаточное условие компланарности.
Слайд 159
Ключевые понятия
Прямая, нормаль, направляющий вектор,
угол между
двумя прямыми,
расстояние от точки
до прямой.
Слайд 160
Вопросы для самопроверки
по теме «Прямая на плоскости»
1.Различные способы
задания прямой на плоскости.
2. Угол между двумя прямыми.
3. Условия
параллельности и перпендикулярности двух прямых.
Слайд 162
Кривые второго порядка.
Уравнение такого вида может определять:
эллипс (в частности, окружность), гиперболу, параболу, пару прямых (параллельных,
пересекающихся либо совпадающих), точку или не определять никакой линии.
Слайд 163
Эллипс
Эллипсом называется геометрическое место
точек (плоскости), сумма расстояний которых от двух данных точек,
называемых фокусами этого эллипса, есть величина постоянная.
Слайд 166
Определение гиперболы
Гиперболой называется
геометрическое место точек,
разность расстояний которых от
двух
данных точек плоскости, называемых
фокусами, есть величина постоянная
Слайд 169
Лекция11.Определение параболы
Параболой
называется
геометрическое место
точек,равноудаленных от данной точки
плоскости, называемой фокусом, и
данной прямой, называемой
директрисой .
Слайд 175
Вопросы для самопроверки
по теме «Кривые второго порядка»
Каноническое уравнения
окружности.
Каноническое уравнение эллипса.
Определение эллипса.
4. Определение гиперболы.
5.
Каноническое уравнение гиперболы.
Слайд 176
Вопросы для самопроверки
по теме «Кривые второго порядка»
(продолжение)
6.Определение параболы.
Канонические уравнения параболы.
7. Приведение общего уравнения кривой второго порядка
к каноническому виду.
Слайд 186
Ключевые понятия
Плоскость, угол между плоскостями,
параллельность плоскостей,
перпендикулярность
плоскостей.
Слайд 187
Вопросы для самопроверки
по теме «Плоскость»
1.Общее уравнение плоскости. Частные
случаи.
2. Уравнение плоскости, проходящей через три данные точки.
3. Условия
параллельности и перпендикулярности двух плоскостей.
Слайд 198
Ключевые понятия
Прямая в пространстве, угол между
прямыми в пространстве,
параллельность прямых,
перпендикулярность прямых,
угол между прямой и плоскостью.
Слайд 199
Вопросы для самопроверки
по теме «Прямая в пространстве»
1. Прямая
в пространстве. Способы задания.
2. Угол между двумя прямыми.
3. Условия
параллельности и перпендикулярности двух прямых.4. Взаимное расположение прямой и плоскости.
Слайд 201
Цилиндрические поверхности
Цилиндрической поверхностью называется
поверхность, составленная из всех прямых, пересекающих данную линию
L и параллельных данной прямой . Линия L при этом называется направляющей цилиндрической поверхности , а каждая из прямых, составляющих поверхность и параллельных прямой , ее образующей.
Слайд 202
Цилиндрические поверхности
Если направляющая цилиндрической поверхности
лежит в одной из координатных
плоскостей , а образующие параллельны координатной оси, перпендикулярной этой плоскости, то уравнение такой поверхности совпадает с уравнением направляющей L, то есть содержит только две переменных.
Слайд 204
Конические поверхности
Конической поверхностью называется поверхность, составленная из
всех прямых, пересекающих данную линию L и проходящих
через данную точку Р. Линия L при этом называется направляющей конической поверхности, точка Р – ее вершиной, а каждая из прямых, составляющих коническую поверхность, - ее образующей.
Слайд 214
Ключевые понятия
Поверхность, эллипсоид, конус,
цилиндр, виды цилиндров,
однополостный гиперболоид,
двуполостный гиперболоид,
параболоид.
Слайд 215
Вопросы для самопроверки по теме «Поверхности второго порядка»
1.
Поверхности второго порядка и их канонические уравнения.
2. Общее уравнение
поверхности второго порядка и его приведение к каноническому виду.
Слайд 225
Ключевые понятия
Замечательные кривые, кривая Гаусса,
Декартов лист,
циссоида Диоклеса,
лемниската Бернулли, циклоида,
астроида, кардиоида.
Слайд 226
Лекция16.Комплексные числа.
Комплексным числом z называется
где x и y–вещественные числа.
Слайд 227
Комплексные числа (продолжение)
называется алгебраической формой
записи комплексного числа.
Слайд 228
Комплексные числа (продолжение)
Число x называется действительной
частью, y–мнимой частью комплексного числа z. Это записывают следующим
образом:
x=Rez, y=Imz.
Слайд 229
Комплексные числа (продолжение)
Если x=0, то число
z называют чисто мнимым; если y=0 , то получается
вещественное число z=x +0i.Два комплексных числа
и называются сопряженными.
Слайд 230
Комплексные числа (продолжение)
Два комплексных числа
и
равны друг другу, если
и ; комплексное число z считается
равным нулю, если x=y=0.
Слайд 231
Комплексные числа (продолжение)
Всякое комплексное число можно
изобразить точкой на плоскости, т.к.
каждому
z соответствуетупорядоченная пара вещественных
чисел (x;y).
Слайд 239
Ключевые понятия
Мнимая единица, комплексное число,
действительная и мнимая части
комплексного
числа; алгебраическая,
тригонометрическая и показательная
формы комплексного числа.
Слайд 240
Вопросы для самопроверки по
теме «Комплексные числа»
1. Формы
записи комплексного числа.
2. Сложение, умножение, деление комплексных чисел.
Слайд 241
Вопросы для самопроверки по
теме «Комплексные числа»
3. Модуль
и сопряженное комплексного числа и их свойства.
4. Возведение комплексного
числа в степень. Формула Муавра.
Слайд 242
Вопросы для самопроверки по
теме «Комплексные числа»
(продолжение)
5. Извлечение корня
из комплексного числа.
6. Основная теорема алгебры.
7. Геометрическое изображение комплексного
числа.
Слайд 243
Основная литература
1. Беклемишев Д.В. Курс аналитической геометрии
и линейной алгебры. – М.: Наука, 2006.
2. Данко П.Е.,
Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 2005, ч.1.
Слайд 244
Основная литература
3. Краснов М.Л., Киселев А.И., Макаренко
Г.И., Шикин Е.В., Заляпин В.И., Соболев С.К. Вся высшая
математика: Учебник. Т. 1. – М.: Эдиториал УРСС, 2007.4. Минорский В.П. Сборник задач по высшей математике. Изд. 3 – 11. Гостехиздат, 1955 – 1957. – М.: Наука, 1964 – 1971.