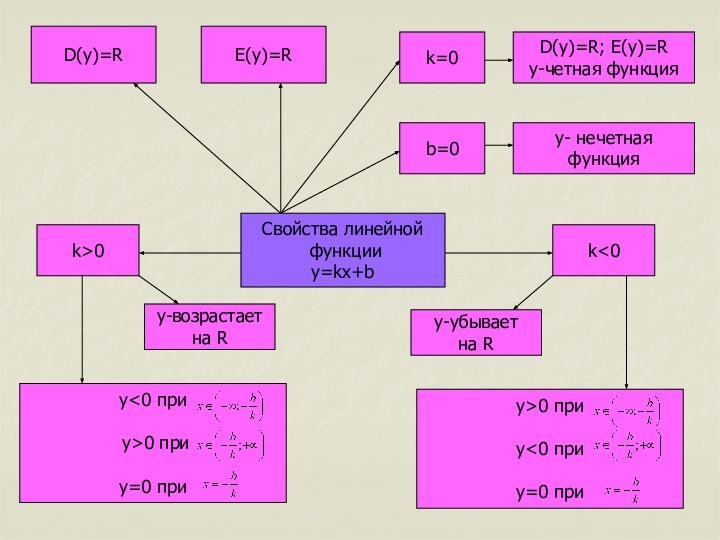
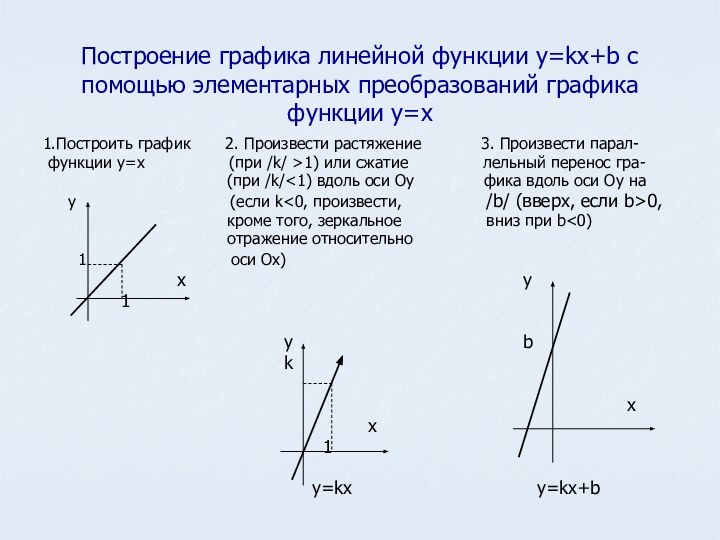
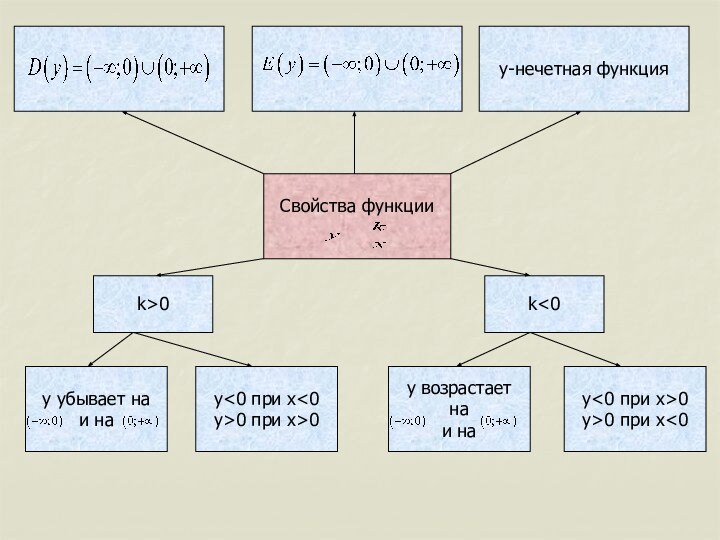
формулой вида y=kx+b, де x-независимая переменная,k и b-некоторые числа.
Графиком
линейной функции является прямая.у Угловой коэффициент k= tg
b – ордината точки пересечения графика
b с осью Оу
х
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


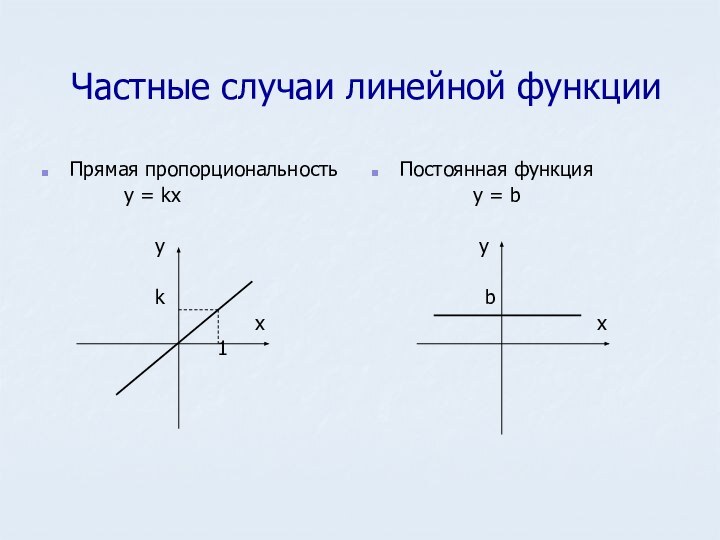



Постоянная функция
y = b
у
b
х
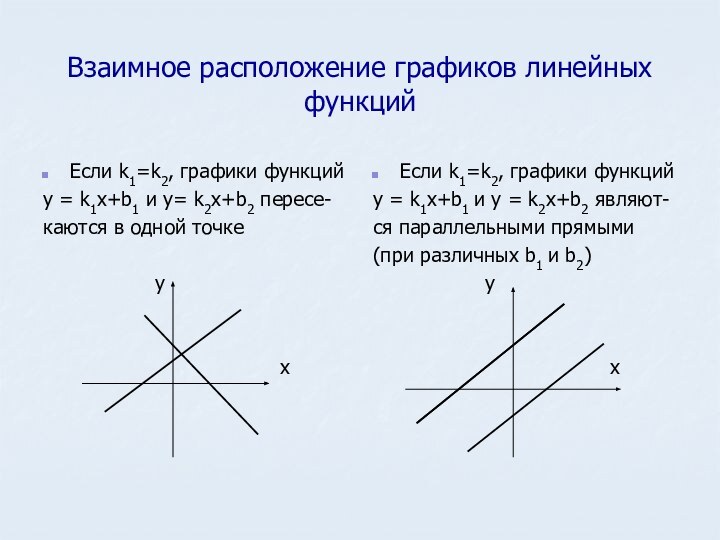
Если k1=k2, графики функций
y = k1x+b1 и y = k2x+b2 являют-
ся параллельными прямыми
(при различных b1 и b2)
у
х