- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Линейная регрессия и корреляция: смысл и оценка параметров
Содержание
- 2. F критерий Фишера - оценивает качество уравнения
- 3. Расчету F-критерия предшествует анализ дисперсии.Центральное место в
- 4. Любая сумма квадратов отклонений связана с числом
- 5. Для расчета df объясненной суммы квадратов имеем:Число степеней свободы равно 1.
- 6. Число степеней свободы остаточной суммы квадратов =
- 7. дисперсии на одну степень свободы
- 8. Значение F-критерия признается достоверным, если оно больше табличного. В этом случае гипотеза H0 отклоняется.
- 9. Если FтаблFфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
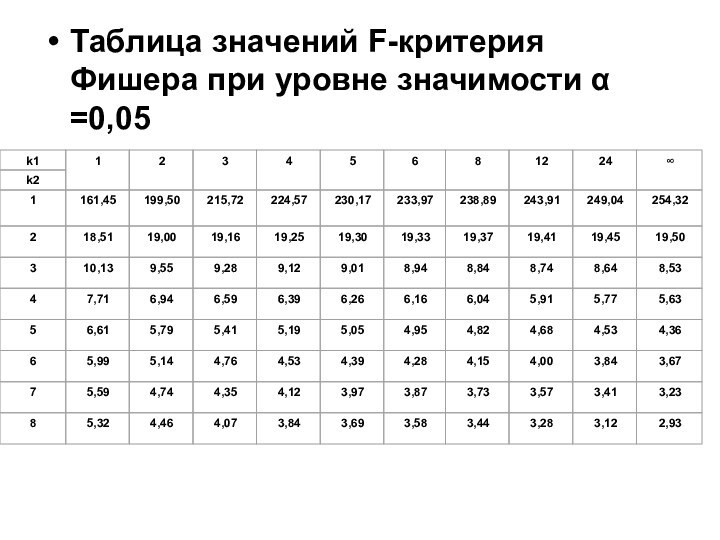
- 11. Таблица значений F-критерия Фишера при уровне значимости α =0,05
- 12. ПРИМЕР (количество факторов – 1)Дисперсионный анализ результатов регрессии
- 13. Для оценки статистической значимости коэффициентов регрессии и
- 15. Сравнивая фактическое и критическое (табличное) значения t-статистики
- 16. доверительный интервал для расчета доверительного интервала определяем
- 17. Если в границы доверительного интервала попадает ноль,
- 18. Скачать презентацию
- 19. Похожие презентации
F критерий Фишера - оценивает качество уравнения регрессии - состоит в проверке гипотезы Но (о том, что коэффициент регрессии равен нулю, т.е. b=0, т.е. фактор х не оказывает влияния на результат у ).









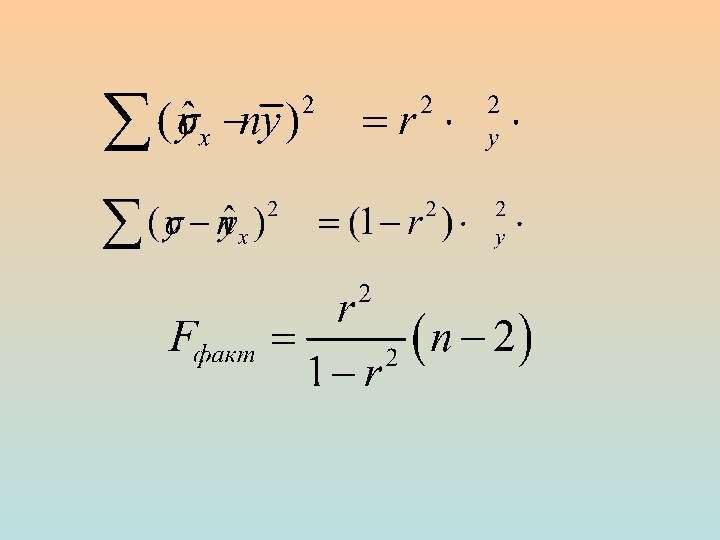


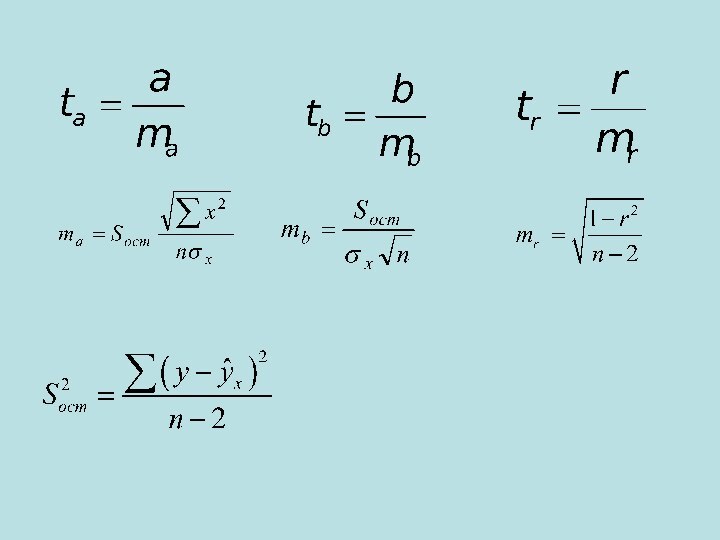




Слайд 3
Расчету F-критерия предшествует анализ дисперсии.
Центральное место в нем
занимает разложение общей суммы квадратов отклонений на две части
«объясненную» и «необъясненную».Общая объясненная остаточная
(необъясненная)
Слайд 4 Любая сумма квадратов отклонений связана с числом степеней
свободы – df, т.е. с числом свободы независимого варьирования
признака.Для общей суммы квадратов требуется (n-1) число отклонений.
Слайд 6 Число степеней свободы остаточной суммы квадратов = число
степ. свободы для общей суммы квадратов – число степ.
свободы для объясненной регрессии.
Слайд 8
Значение F-критерия признается достоверным, если оно больше табличного.
В этом случае гипотеза H0 отклоняется.
Слайд 9 Если Fтабл
природе оцениваемых характеристик отклоняется и признается их статистическая значимость
и надежность.Если Fтабл>Fфакт, то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Слайд 13 Для оценки статистической значимости коэффициентов регрессии и корреляции
рассчитываются t-критерий Стьюдента каждого из показателей и доверительные интервалы.
Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Слайд 15 Сравнивая фактическое и критическое (табличное) значения t-статистики -
tтабл и tфакт - принимаем или отвергаем гипотезу Но.
Если
tтабл < tфакт то гипотеза Ho - о незначимости параметра отклоняется, т.е. a, b и не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tтабл > tфакт то гипотеза Но не отклоняется и признается случайная природа формирования а, b или rxy .
Слайд 16
доверительный интервал
для расчета доверительного интервала определяем предельную
ошибку Δ для каждого показателя
для коэффициентов регрессии границы
доверительного интервала составят:





























