Слайд 2
Функция y = loga х (где а >
0, а =1) называется логарифмческой.
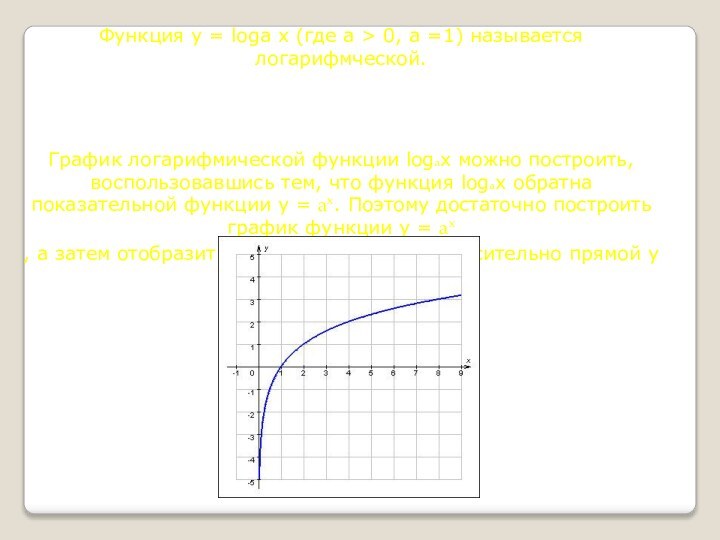
График логарифмической функции logaх можно
построить, воспользовавшись тем, что функция logaх обратна показательной функции y = ax. Поэтому достаточно построить график функции y = ax
, а затем отобразить его симметртрично относительно прямой у = х.
Слайд 3
Свойства функции у = logaх
у = logaх при
a > 1;
1.D(f) = (0; + ∞);
2.не является
ни четной, ни нечетной;
3.возрастает на (0; + ∞);
4.не ограничена сверху, не ограничена снизу;
5.не имеет ни наибольшего, ни наименьшего значений;
6.непрерывна;
7.E(f) = (- ∞;+ ∞ );
8.выпукла вверх;
9.дифференцируема.
y = logaх при 0 < a < 1;
1.D(f) = (0;+ );
2.не является ни четной, ни нечетной;
3.убывает на (0; +);
4.не ограничена сверху, не ограничена снизу;
5.нет ни наибольшего, ни наименьшего значений;
6.непрерывна;
7.E(f) = (-;+ );
8.выпукла вниз;
9.дифференцируема.
Слайд 4
ПОСТРОЕНИЕ ГРАФИКОВ
Изобразить график функции y=ln(x+1)-1.
График функции получается в
результате сдвига графика функции y = ln x на
одну единицу влево (при этом мы получаем функцию y = ln (x + 1)) и на одну единицу вниз
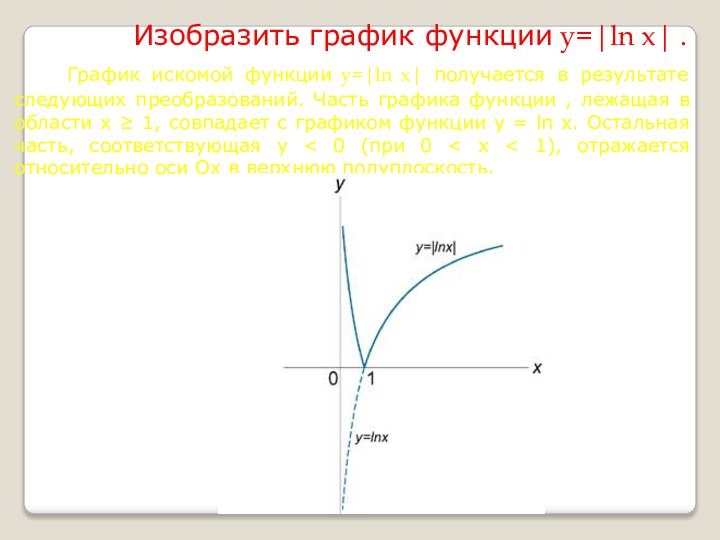
Изобразить график функции y=|ln x| .
График искомой
функции y=|ln x| получается в результате следующих преобразований. Часть графика функции , лежащая в области x ≥ 1, совпадает с графиком функции y = ln x. Остальная часть, соответствующая y < 0 (при 0 < x < 1), отражается относительно оси Оx в верхнюю полуплоскость.
Слайд 6
Изобразить график функции y=|ln|x||.
Сначала мы построим график функции
y=|ln x| , как описано в предыдущем примере. Затем
отразим график этой функции относительно оси Оy в левую полуплоскость. Совокупность этих графиков и представляет собой график искомой функции
Слайд 7
Основные методы решения уравнений
Слайд 8
Методы решения уравнений:
функционально графический метод ;
по определению логарифма;
потенцирование;
замена
переменных;
логарифмирование
Слайд 9
Функционально графический метод
Пример №1: решите уравнение
Log5 x=0 Решение:
Уравнение
log5 x=0 имеет один корень x=1,поскольку график функции y=log5
x
пересекает ось х в единственной точке (1;0).
Слайд 10
Логарифмические уравнения
Логарифмическими уравнениями называют уравнения вида
loga f(x) = loga g(x), где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
Слайд 11
По определению логарифма:
loga x=в
x=a , где а≠1 и
а>0
в
Слайд 12
Пример:
logx16=2
x =16
х≠1
х>0
х1 = 4
х2 = - 4
– не удовлетворяет условию х>0
Ответ: 4
2
Слайд 13
Потенцирование
loga f(x) = loga g(x)
f(x) = g(x),
f(x) >
0,
g(x) > 0
Слайд 14
Пример:
logx (x-1) = logx (2x-8)
X-1 = 2x-8,
x=7,
X-1>0,
x>1,
2x-8>0, x>4,
x≠1, x≠1,
x>0 x>0
x=7 удовлетворяет всем условиям системы
Ответ: 7
Слайд 15
Замена переменных:
loga f(x) + loga f(x) + c=0,
loga
f(x) = t, f(x)>0
t + t + c = 0
Далее решаем квадратное уравнение
Д = t - 4*a*c
Находим t1 и t2
Подставляем значения t1 и t2:
2
2
loga f(x)=t1
loga f(x)=t2
Слайд 16
Пример:
2*log0,3 – 7*log0,3 -4 = 0
log0,3 x =
t, x>0
2t - 7t - 4 = 0,
Д =
49 + 32 = 81,
t1 = (7+9) / 4 = 4,
t2 = (7-9) / 4 = -1/2
log0,3 x = 4, log0,3 x = -1/2,
x1 = 0,0081 x2 = √30 / 3
Ответ: 0,0081; √30 / 3
2
2
Слайд 17
Логарифмирование:
f(x) = g(x)
f(x)>0,
g(x)>0
loga f(x) = loga g(x)
Слайд 18
Пример:
x = 0,04
Прологарифмируем обе части по основанию 5.
log5x
= log50,04
Учтем, что log5x = r*log5x и что log50,04 = -2, следовательно уравнение можно привести к следующему виду:
(1-log5x) * log5x = -2
log5x = y
(1-y) * y = -2
y² - y – 2 = 0,
log5x = 2, log5x = -1
x = 25 x = 1/5
Ответ: 1/5; 25
1- log5x
1- log5x
r
Слайд 19
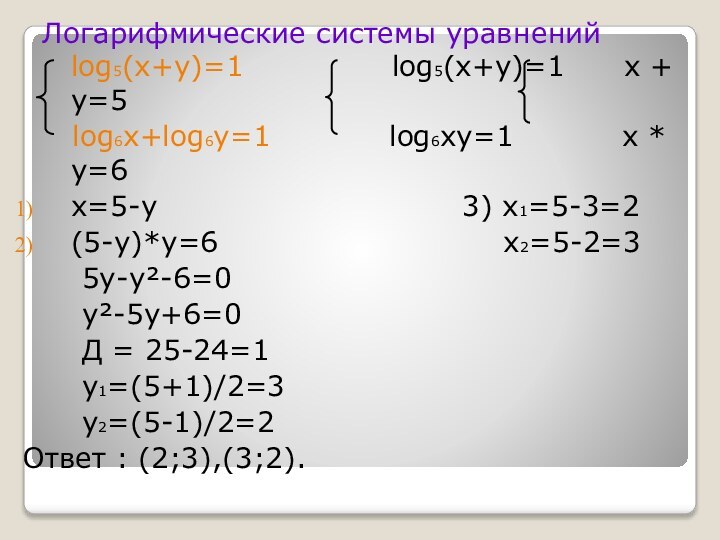
Логарифмические системы уравнений log5(x+y)=1
log5(x+y)=1 x +
y=5
log6x+log6y=1 log6xy=1 x * y=6
x=5-y 3) x1=5-3=2
(5-y)*y=6 x2=5-2=3
5y-y²-6=0
y²-5y+6=0
Д = 25-24=1
y1=(5+1)/2=3
y2=(5-1)/2=2
Ответ : (2;3),(3;2).
Слайд 21
1) loga f(x) > loga g(x)
Неравенство, содержащее
неизвестное под знаком логарифма или (и) в его основании,
называется логарифмическим неравенством.
Логарифмические неравенства
f(x)>g(x)>0,
a>1.
00
2) logh(x) (x)>logh(x)g(x)
f(x)>g(x)>0,
h(x)>1.
00
Равносильные преобразования
Слайд 22
3) logh(x)f(x)>logh(x)g(x)
(h(x)-1)(f(x)-g(x))>0,
h(x)>0,
f(x)>0,
g(x)>0.
Пример: log7-x(x2 -5x+6)>log7-x (2x-4)
Решение: (7-x-1)(x2-5x+6-2x+4)>0
7-x>0,
7-x≠1,
x2 -5x+6>0,
2x-4>0.
xє(5;6)
Слайд 23
4) logab - logcb>0
(a-1)(b-1)(c-1)(c-a)>0,
a>0,a≠1,
c>0,c≠1,
b>0.
Пример:
logx(x-1)
- logx+1(x-1)0,
x+1>0.
x(x-1)(x-2)1.
xє(1;2)
Слайд 24
5) f(logax)>0
t=logax,
f(t)>0.
6) logab × logcd>0
(a-1)(b-1)(c-1)(d-1)>0,
a>0,a≠1,
b>0,
c>0,c≠1,
d>0.
Замена переменной
Слайд 26
В3. Найдите корень уравнения 2-lg(10-x)=0.
Решение.
Найдем О.Д.З.: x
уравнение:
-lg(10-x)=-2
lg(10-x)=2
Решим получившееся уравнение по определению логарифма:
10-x=102
-x=90
x=-90.
Найденный корень
уравнения удовлетворяет О.Д.З.
Ответ: -90 .
Слайд 27
В4. Найти значение выражения (logа(b3)*logba)/(a*b), если a=3, b=5
Решение.
Преобразуем
числитель:
loga(b3)*logba = logbb3 = 3*logbb = 3
У нас
получилось следующее выражение: 3/(a*b)
Теперь подставим значения a и b в получившееся выражение: 3/(3*5)=0,2 .
Ответ: 0,2 .
Слайд 28
В11. Найдите наибольшее значение функции y=log1/3 √(x3) на
отрезке [1/3;3]
Решение.
Рассмотрим функцию y=log1/3f(x) – она убывающая, следовательно
принимает наибольшее значение при наименьшем значении функции f(x).
Функция f(x)=√(x3) возрастающая и определена на промежутке (0;+∞), т.е. наименьшее значение принимает при наименьшем значении x.
yнаиб=y(1/3)=log1/3√(1/27)=log1/3(1/3)3/2=3/2*log1/3(1/3)=1,5
Ответ: 1,5.
Слайд 29
С3. Решите неравенство 7^log72x+x^log7x0.
Представим x как
7^log7x и подставим в данное неравенство:
7^log72x+ 7^log72x
решим его:
2* 7^log72x<14
7^log72x<7, 7>1
log72x<1
-11/7Данный промежуток удовлетворяет О.Д.З.
Ответ: (1/7;7) .
Слайд 30
САМОСТОЯТЕЛЬНАЯ РАБОТА В ВИДЕ ТЕСТА (ПРИМЕРЫ ИЗ ВАРИАНТОВ
ЕГЭ)
1. Вычислите:
1. Вычислите:
1)8 2)2 3)3 4)4 1)13 2)2 3)17 4)-169
2. 2.
1)-6 2)6/49 3)6 4) а-49 1)-1 2)9 3)4 4)0,8
3. Вычислите: 3.Вычислите:
1)13 2)9 3)22 4)5 1)17 2)4 3)14 4)23
4. Найдите область определения функции
4. 4.
5. Вычислите: 5. Вычислите:
Составьте число из номеров правильных ответов.
Проверим ответы.
Слайд 32
Звезды, шум и логарифмы
Заголовок этот, связывающий столь, казалось
бы, несоединимые вещи, не притязает быть пародией на произведения
Кузьмы Пруткова; речь в самом деле пойдет о звездах и о шуме в тесной связи с логарифмами.
Слайд 33
Звезды, шум и логарифмы
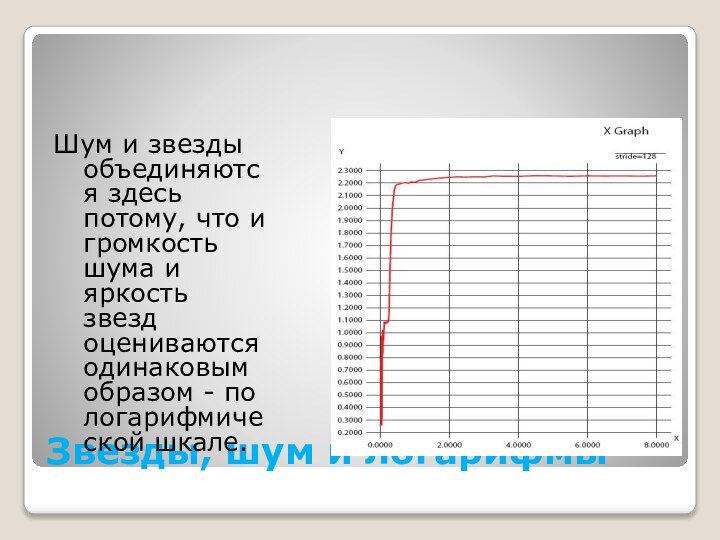
Шум и звезды объединяются здесь
потому, что и громкость шума и яркость звезд оцениваются
одинаковым образом - по логарифмической шкале.
Слайд 34
Звезды, шум и логарифмы
Астрономы распределяют звезды по степеням
видимой яркости на светила первой величины, второй величины, третьей
и т. д. Последовательные звездные величины воспринимаются глазом как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой не что иное, как логарифм ее физической яркости. Звезда, например, третьей величины ярче звезды первой величины в 2,53-1, т. е. в 6,25 раза.
Короче говоря, оценивая видимую
яркость звезд, астроном оперирует
с таблицей логарифмов, составленной
при основании 2,5.
Слайд 35
Звезды, шум и логарифмы
Сходным образом оценивается и громкость
шума. Вредное влияние шумов на здоровье людей побудило изучению
шумов,к их классификации, к созданию определённых стандартов и эталонов. Единицей громкости служит «бел», практически - его десятая доля, «децибел». Последовательные степени громкости - 1 бел, 2 бела и т. д. (практически- 10 децибел, 20 децибел и т. д.)--составляют для нашего слуха арифметическую прогрессию. Физическая же «сила» этих шумов (точнее - энергия) составляет прогрессию геометрическую со знаменателем 10. Разности громкостей в 1 бел отвечает отношение силы шумов 10. Значит, громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.
Слайд 36
Звезды, шум и логарифмы
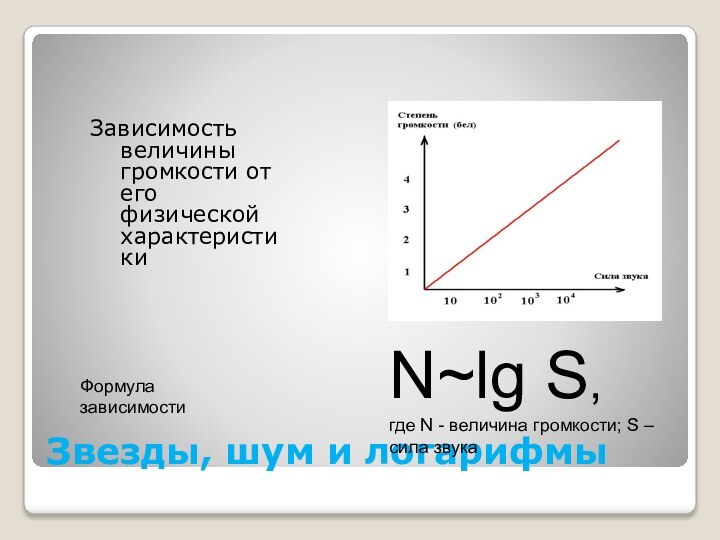
Зависимость величины громкости от его
физической характеристики
Формула зависимости
N~lg S,
где N - величина громкости;
S – сила звука
Слайд 37
Звезды, шум и логарифмы
Шум, громкость которого больше 8
бел, признается вредным для человеческого организма.
Указанная норма
на многих заводах превосходится: здесь бывают шумы в 10 и более бел; удары молотка в стальную плиту порождают шум в 11 бел.
Случайность ли то, что и при оценке видимой яркости светил и при измерении громкости шума мы имеем дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения? Нет, то и другое - следствие общего закона (называемого «психофизическим законом Фехнера»), гласящего: величина ощущения пропорциональна логарифму величины раздражения.
Слайд 38
Музыка и логарифмы
Никто и предположить не мог, что
музыка и логарифмы связаны между собой. Известный физик Эйхенвальд
вспоминал: “Товарищ мой по гимназии любил играть на рояле, но не любил математику. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом не имеют ничего общего. “Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, - но ведь как раз пифагорова – то гамма для нашей музыки и оказалась неприемлемой”. Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах”.
Слайд 39
Музыка и логарифмы
Зависимость частоты колебаний ноты «до» в
разных октавах:
Номер октавы
Частота
0 n
1 2n
2 nx22
… …
m nx2m
























![Логарифмические уравнения и их системы В11. Найдите наибольшее значение функции y=log1/3 √(x3) на отрезке [1/3;3]Решение. Рассмотрим функцию](/img/tmb/13/1266243/63e9ca4e7c6675ffbfb5b2969e266f79-720x.jpg)