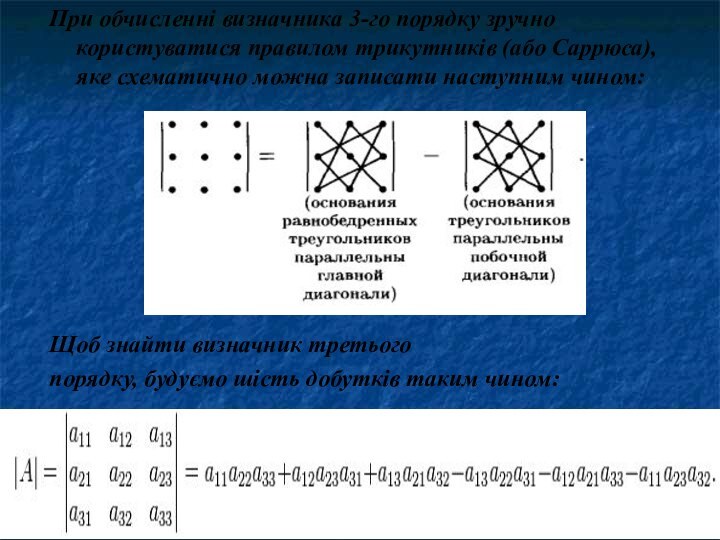
можно зіставити число detA (
), яке називається її визначником (детермінантом) наступним чином:
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Визначник другого та третього порядків
Содержание
- 2. ПланВизначникиМінориАлгебраїчні доповнення
- 3. Визначники До квадратної матриці А порядку
- 5. На відміну від матриці визначник обмежується справа та зліва одинарною лінією.
- 6. Щоб знайти визначник другого порядку,множимо елементи головної
- 7. Приклад:
- 8. При обчисленні визначника 3-го порядку зручно користуватися
- 9. Приклад:
- 10. Властивості визначників1. Значення визначника не змінюється,якщо всі його рядки замінити відповідними стовбцями. Така операція називається транспонуванням.
- 11. 2. Перестановка двох рядків визначника рівносильна множенню
- 12. 4. Якщо всі елементи якого-небудь рядка, або
- 13. 6. Якщо відповідні елементи двох рядків визначника
- 14. 8. Якщо кожен елемент деякого рядка визначника
- 15. МінориОзначення. Мінором Мij, що відповідає елементу аij
- 16. Алгебраїчні доповненняОзначення. Алгебраїчним доповненням Аij, що відповідає
- 17. Приклад: Дано матрицю Обчислити мінори М12 і М22 та алгебраїчні доповнення А12 і А22.
- 18. Алгебраїчні доповнення: теореми.Теорема 1. (Теорема Лапласа) Значення
- 19. Приклад: Обчислити визначник розкладаючи його за елементами третього рядка:
- 20. Теорема 2. Сума добутків елементів будь-якого рядка
- 21. Скачать презентацию
- 22. Похожие презентации
ПланВизначникиМінориАлгебраїчні доповнення
Слайд 6
Щоб знайти визначник другого порядку,
множимо елементи головної діагоналі
та
віднімаємо добуток елементів побічної
діагоналі:
Обчислення визначника другого порядку ілюструється
схемою:Слайд 8 При обчисленні визначника 3-го порядку зручно користуватися правилом
трикутників (або Саррюса), яке схематично можна записати наступним чином:
Щоб
знайти визначник третього порядку, будуємо шість добутків таким чином:
Слайд 10
Властивості визначників
1. Значення визначника не змінюється,
якщо всі його
рядки замінити відповідними стовбцями. Така операція називається
транспонуванням.
Слайд 11 2. Перестановка двох рядків визначника рівносильна множенню його
на -1.
3. Якщо визначник має два однакових
рядки, або
стовпці, то він дорівнює нулю.
Слайд 12
4. Якщо всі елементи якого-небудь рядка, або
стовпця
визначника містять спільний множник,
то його можна винести за знак
визначника.5. Якщо всі елементи деякого рядка, або
стовпця визначника дорівнюють нулю, то
сам визначник дорівнює нулю.
Слайд 13
6. Якщо відповідні елементи двох
рядків визначника пропорційні,
то визначник
дорівнює нулю.
7. Якщо до елементів деякого рядка
визначника
додати відповідні елементи іншого рядка, помножені на довільний спільний
множник, то значення визначника при цьому не
зміниться.
Слайд 14
8. Якщо кожен елемент деякого рядка
визначника є
сумою двох доданків, то визначник
може бути зображений у
вигляді суми двох визначників, у яких один у згаданому рядку має
перші з заданих доданків, а інші другі; елементи,
що знаходяться на решті місць у всіх трьох
визначниках одні й ті самі.
Слайд 15
Мінори
Означення.
Мінором Мij, що відповідає елементу аij
матриці,
називається визначник, який
відповідає матриці, утвореній з матриці
викреслюванням
i-го рядка та j-го стовпця.
Слайд 16
Алгебраїчні доповнення
Означення. Алгебраїчним доповненням Аij,
що відповідає елементу
аij матриці,
називається відповідний мінор, взятий зі
знаком “+”,
якщо сума його індексів парна, і зі знаком “-”, якщо сума його індексів
непарна.
Слайд 18
Алгебраїчні доповнення: теореми.
Теорема 1. (Теорема Лапласа)
Значення визначника
п-го порядку, що
визначає матрицю, дорівнює сумі добутків
елементів
довільного рядка або довільного стовпця на відповідні алгебраїчні доповнення.
Для визначника виконуються такі
рівності:
Слайд 20
Теорема 2. Сума добутків елементів будь-якого
рядка або
стовпця визначника на алгебраїчні
доповнення відповідних елементів іншого рядка,
чи стовпця дорівнюють нулю.
